🔍 Problem

11053 가장 긴 증가하는 부분 수열

---

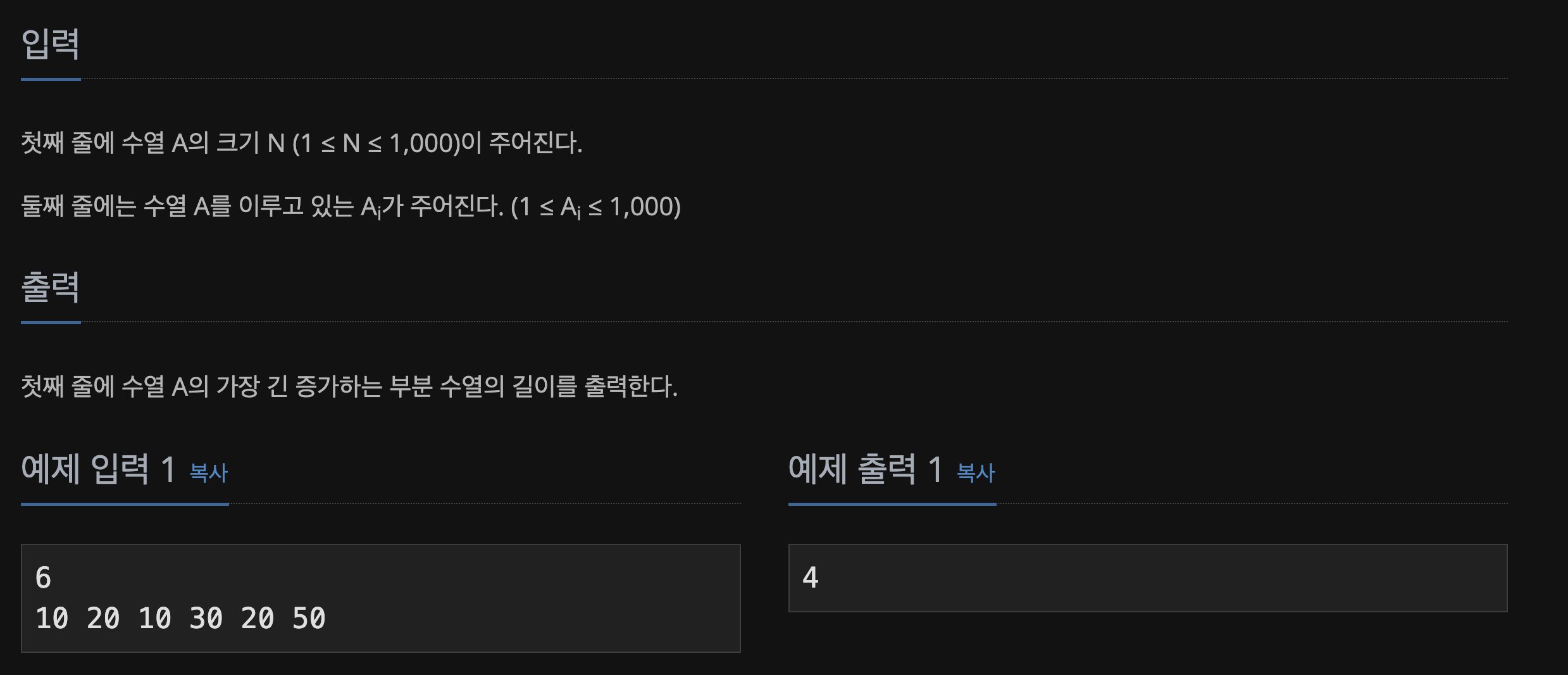
📃 Input&Output

---

📒 해결 과정

1️⃣ 각 수를 포함한 증가하는 수열의 길이를 작성한다.

가. 증가하는 수열의 길이는 자신의 수보다 작은 수의 수열의 길이 값 +1 이다.

예를들어 6번에서 수 50의 dp값은 4이다. 이것은 50보다 작은 4번, 30의 dp 값에서 +1을 한 것이다.

나. 자신보다 작은 수를 찾으려면 전의 수들을 순차적으로 접근하여 대소비교

6번 50인 경우에 1~5번까지의 수를 비교한다.

다. 갱신되는 dp값이 가장 큰 수를 가져온다.

참고로 갱신은 현재 dp, 즉 dp[n]이 되므로
$dp[i]=max(dp[i], dp[i-1]+1)$ 으로 진행한다.

---

💻 Code

import java.util.Scanner;

//https://velog.io/@halo_3735/11053

// dp
// 0 0 0 0 0 0 0

// arr
// 10 20 10 30 20 50


//public class Main {
public class P11053 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int N = sc.nextInt();       // 6
        int[] arr = new int[N+1];   // 10 20 10 30 20 50
        int[] dp = new int[N+1];

        for (int i=1;i<=N;i++){
            arr[i]=sc.nextInt();
        }

        for (int i=1;i<=N;i++){
            dp[i]=1;
        }




        for (int i=2; i<=N;i++){
            int v = arr[i];
            for (int j=1;j<i;j++){
                int pv = arr[j];
                if (v>pv){
                    dp[i]=Math.max(dp[i], dp[j]+1);
                }
            }
        }

        int max_num=0;
        for (int i=1;i<=N;i++){
            if (max_num <dp[i]){
                max_num=dp[i];
            }
        }
        System.out.print(max_num);


    }
}



// 만약 현재 값이 max보다 크다면
//d[i]=dp[i-1]

//else
//dp[i]=dp[i-1]

---

🎸 기타

가. 한 줄 입력

import java.util.Scanner
Scanner sc = new Scanner(System.in);

String line = sc.nextline();

나. 숫자 입력

int N = sc.nextInt();

---

🤔 느낀점

DP를 계속 풀 수록, 놓치고 있는 점이 있다. 바로 끝에서 부터 생각하지 못한다는 점이다. 최선의 값을 만들기 위해서는 이전의 값이 최선이여야 한다는 점을 명심하자. 그리고 그것은 순차적으로 잃어나지 않을 수도 있음을 생각하자.

이 문제의 경우 6번의 50의 dp값은 4번의 30의 dp값(3)으로 부터 갱신됨. (물론 다른 것을 통해 갱신될 수도 있지만, max에서 걸러짐)

---

📝 출처

문어박사의 IT편의점

늘 감사합니다 박사님