[CS224N] Lecture 4 – Backpropagation and computation graphs

지난 시간에, backpropagation 하며 weight matrix를 업데이트하기 위해서는 결과 s를 weight에 대해 미분해야 한다고 배웠었다.

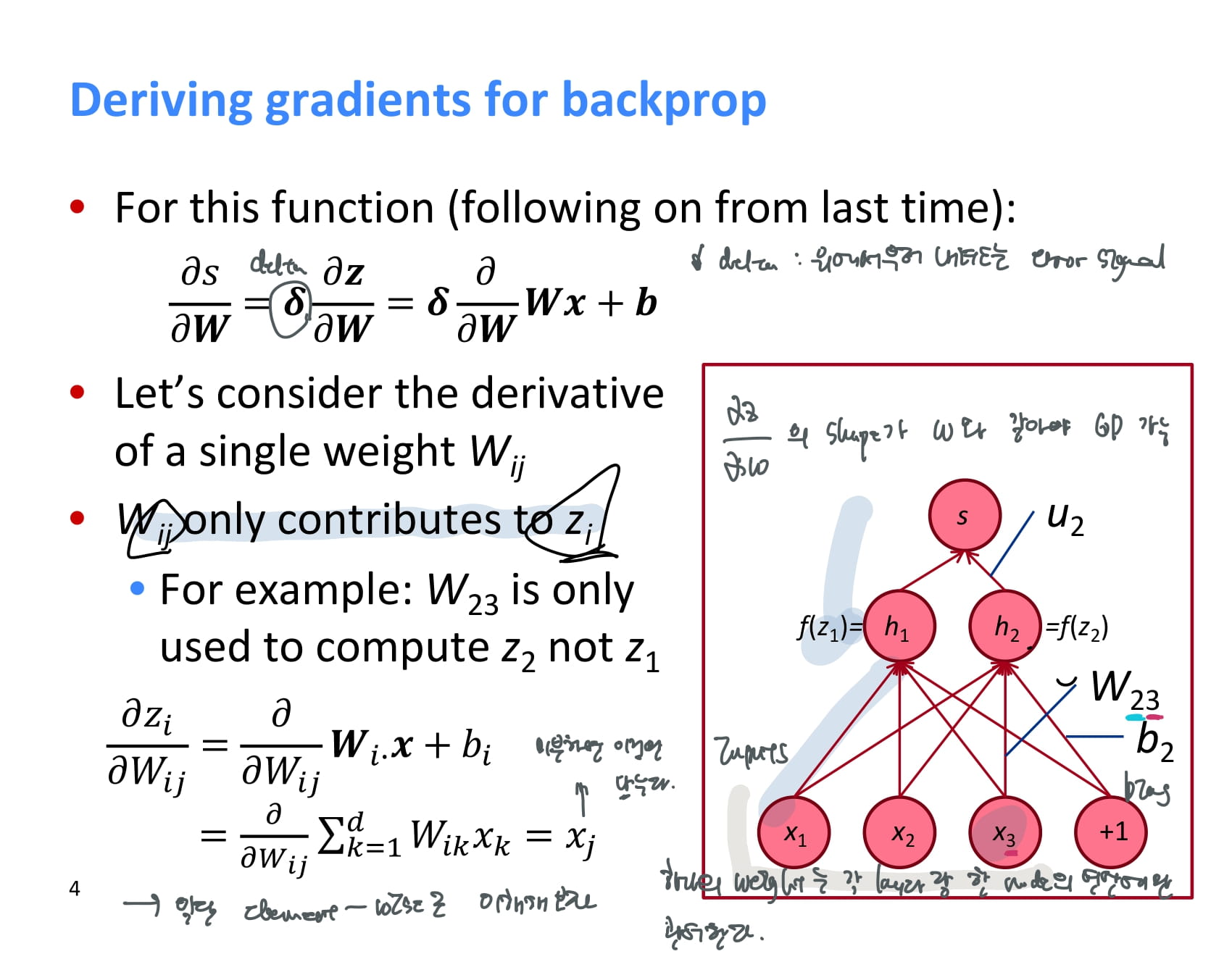
결과 s를 weight에 대해 미분하는 과정을 다시 살펴보자.

$\partial{s}\over\partial{W}$ 는 chain rule을 적용해 ${\partial{s}\over\partial{h}}{\partial{h}\over\partial{z}}{\partial{z}\over\partial{W}}$ 로 계산할 수 있었고, 이 때 ${\partial{s}\over\partial{h}}{\partial{h}\over\partial{z}}$ 을 $\delta$ 라고 했었다. 이 값은 위에서부터 계산되어 내려올 것이다.

그러면 ${\partial{z}\over\partial{W}}$ 는 어떻게 계산할 수 있을까? 일단은 쉽게 원소별 계산으로 이해해보자. 예를 들어, $W_{23}$ 은 $z_2$ 의 계산에만 영향을 준다.

${\partial\over\partial{W_{ij}}}\Sigma^d_{k=1}W_{ik}x_k$ 에서 $k == j$ 인 경우만 고려하면 되기 때문에, $\partial{z_i}\over\partial{W_{ij}}$ 의 값은 $x_j$ 만 남게 된다.

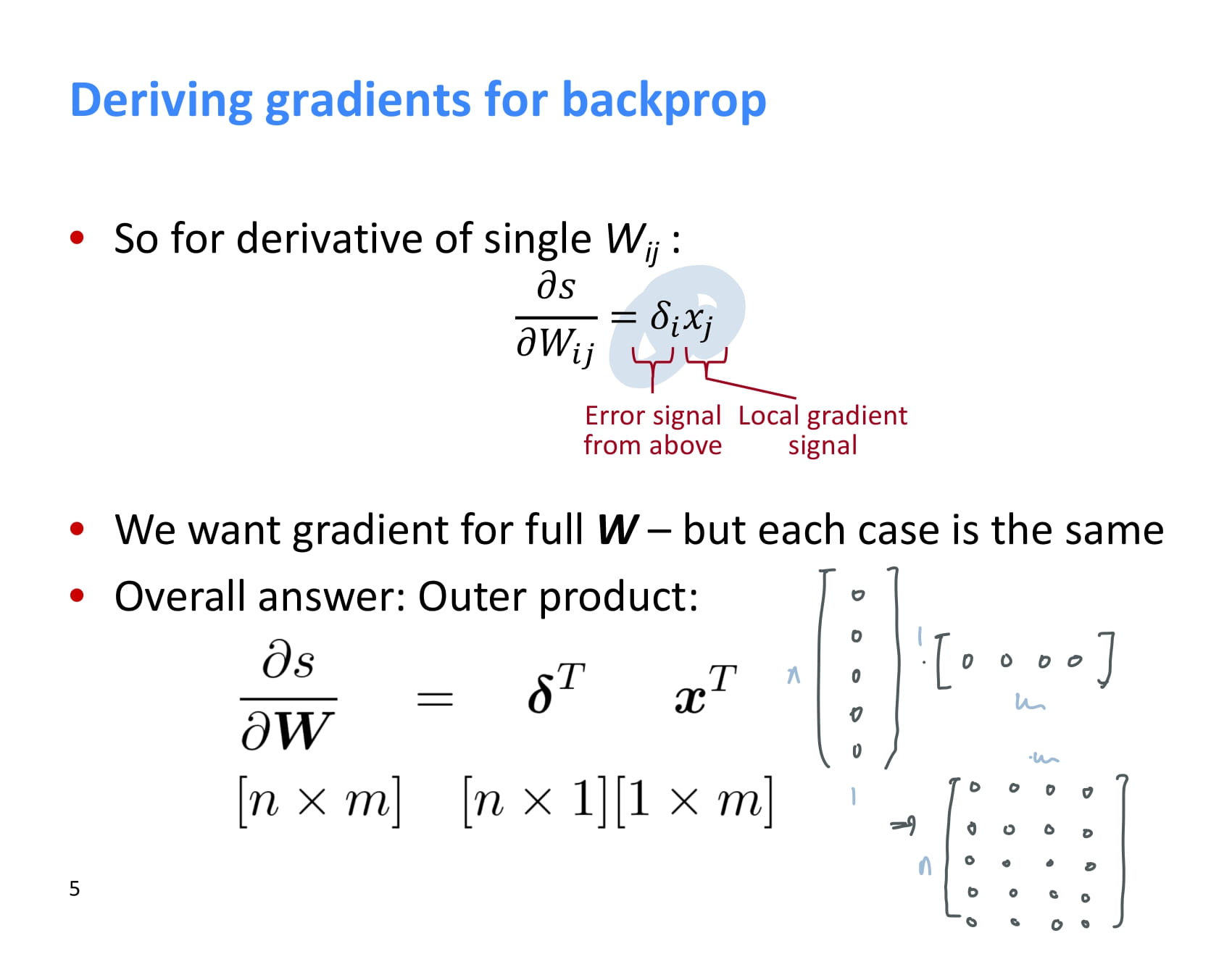
그러므로 하나의 $W_{ij}$ 에 대한 미분값은 다음과 같다.

${\partial{s}\over\partial{W_{ij}}} = \delta_ix_j$

이것을 모든 $W$ 의 element에 적용하는 것은 간단하다. 전체 weight에 대한 $\delta^T$ 와 $x^T$ 를 구한 후, $\delta^T\cdot{x^T}$ 를 계산해 최종 shape만 맞춰주면 된다.

기울기를 구할 때의 팁도 알려주셨다.

1. 차원 수를 잘 트래킹하며 틀리지 않게 유지하기
2. 우리가 하는 건 그저 chain rule을 반복적으로 matrix에 적용하는 것뿐. 쫄지 말자.
3. softmax를 미분할 때에는 correct class와 incorrect class 두 가지 관점에서 생각해보세요.
4. matrix 계산이 어려울 땐 element-wise로 생각하면 낫다.
5. 지난 강의에서 설명한 shape convention을 사용하자.

이렇게 계산된 기울기는 window 내 단어 벡터만 업데이트하게 된다. window 안에 중복 단어가 있는 경우 두 번 업데이트한다.

이렇게 신경망을 이용해 word vector를 업데이트하며 주변 단어를 통한 NER을 수행할 수 있다.

하지만 이렇게 훈련하는 방식이 항상 잘 작동하진 않는다.

(스터디 발표를 하며 필기한 흔적이 남아있어 필기가 조금 더럽다. 하지만 정리하긴 귀찮았다.)

pretrained word vector가 존재하고, 이를 이용해 영화 리뷰를 분류하는 모델을 훈련하려 한다.

예시 그래프에 보이다시피, 훈련 전 TV, telly, television이라는 단어의 벡터는 유사한 상태이다.

하지만 이 때 훈련셋에는 TV와 telly라는 단어만 존재하고 테스트셋에는 television만 존재하는 경우, 이 훈련셋을 이용해 word vector를 업데이트한다면 어떻게 될까?

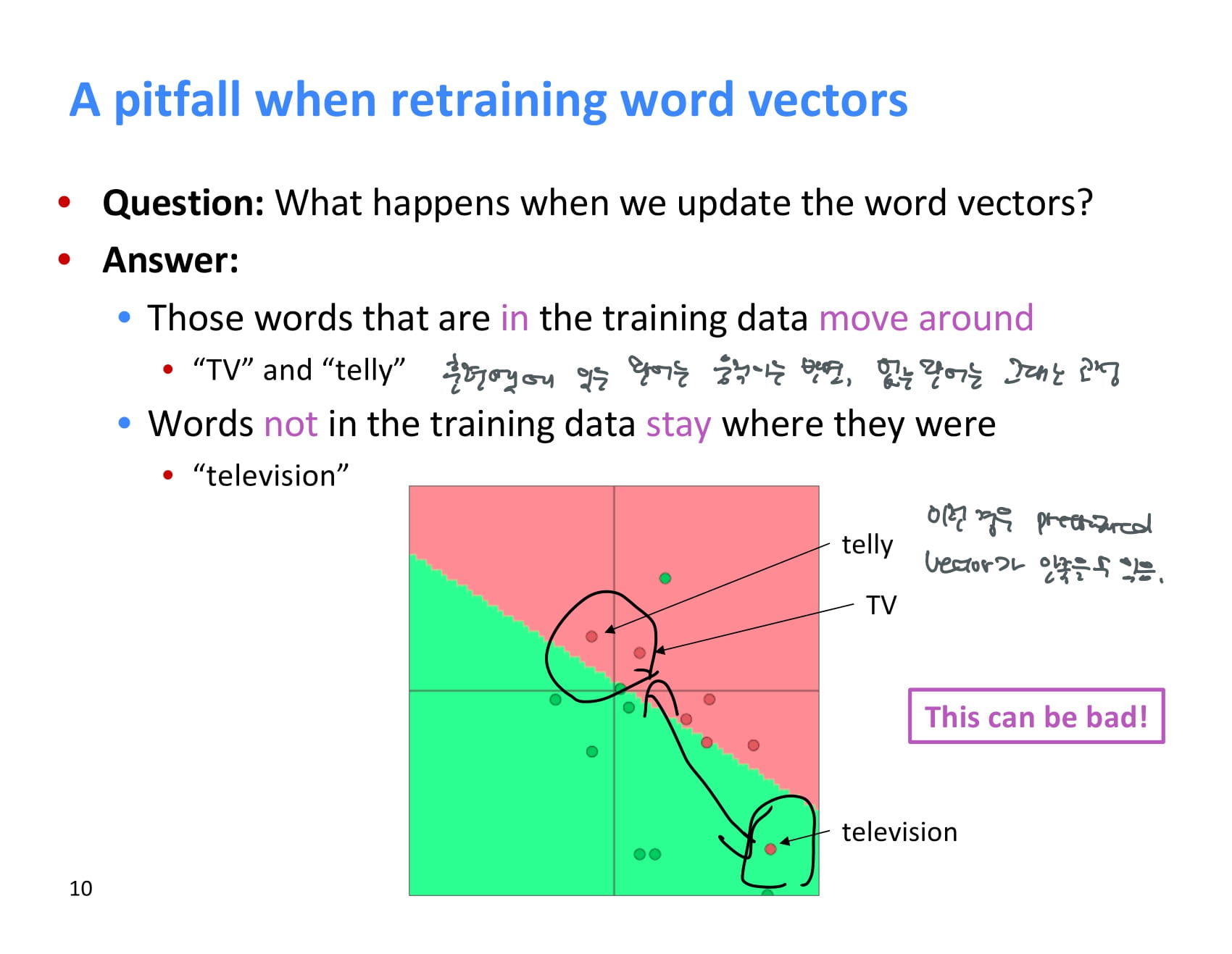
훈련셋에 있는 TV와 telly만 훈련 과정을 통해 이동하고, 테스트셋에만 존재하는 television은 원래 훈련된 위치에 그대로 머무른다.

그래서 pretrained word vector를 쓰지 말라는걸까?

아니다. 사용하는게 좋긴 하다. 일단 pretrained word vector는 단순한 알고리즘으로 훈련이 쉽고, 텍스트 데이터만 있으면 만들 수 있기 때문에 편리하다.

하지만 pretrained word vector를 fine-tune 하는게 좋을지는 데이터 사이즈에 따라 달라진다.

데이터가 적으면 위의 예시처럼 업데이트에서 누락되는 단어가 있을 수 있기 때문에 fine-tune하지 않는것이 낫고, 데이터가 많은 경우 fine-tune 하는 것이 낫다.

이 때 일부 word vector만 업데이트해도 log-likelyhood를 개선할 수는 있다.

지금까지 backpropagation도 거의 둘러봤다.

이제 계산량을 줄이기 위해 미분값을 재사용하는 트릭을 배워보자.

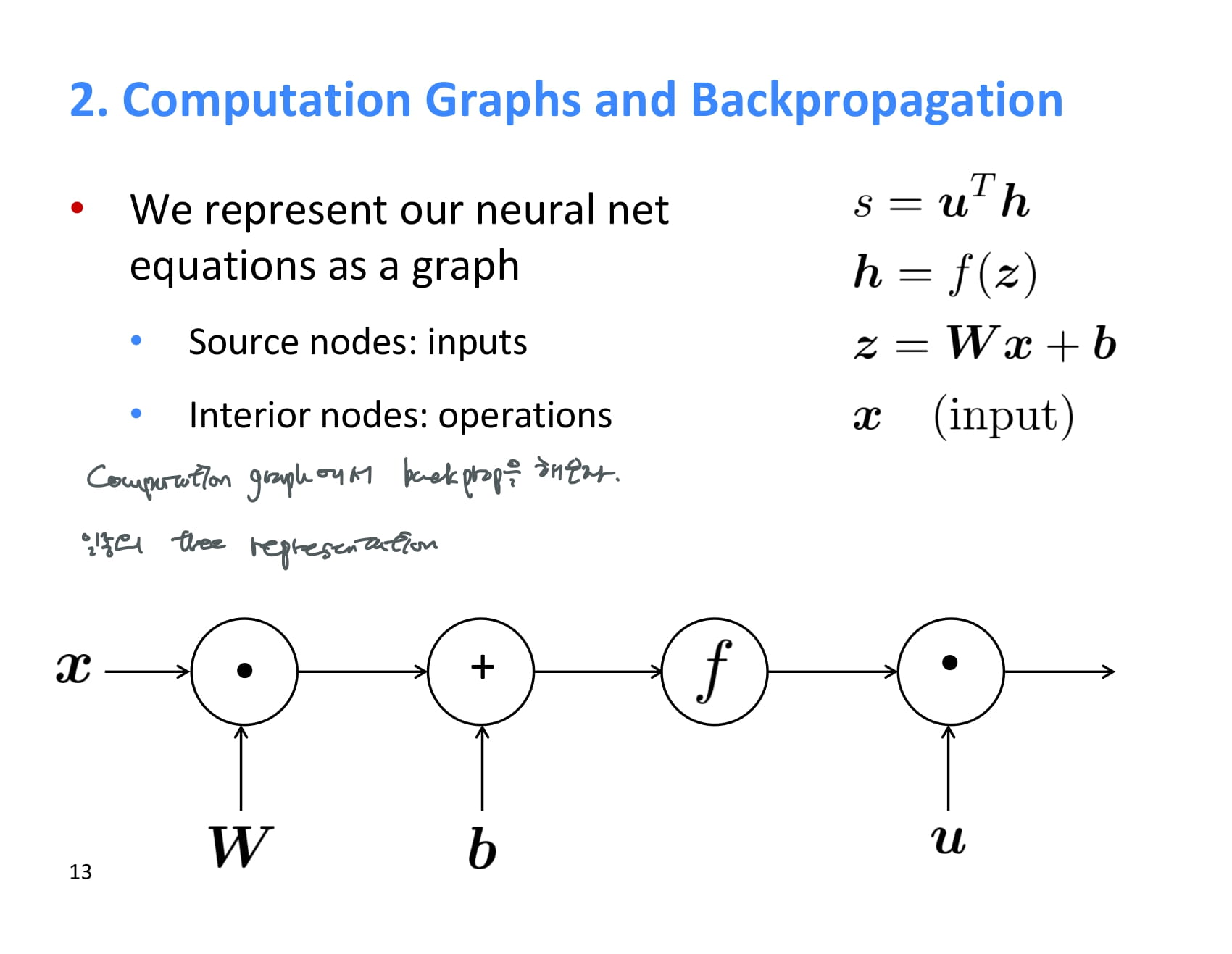
neural net은 이렇게 computation graph로도 나타낼 수 있다. 이렇게 나타내면 forward propagation/back propagaton을 이해하기 쉽다.

여기에서 시작 노드는 input을 의미하고, 내부 노드는 operation을 의미한다.

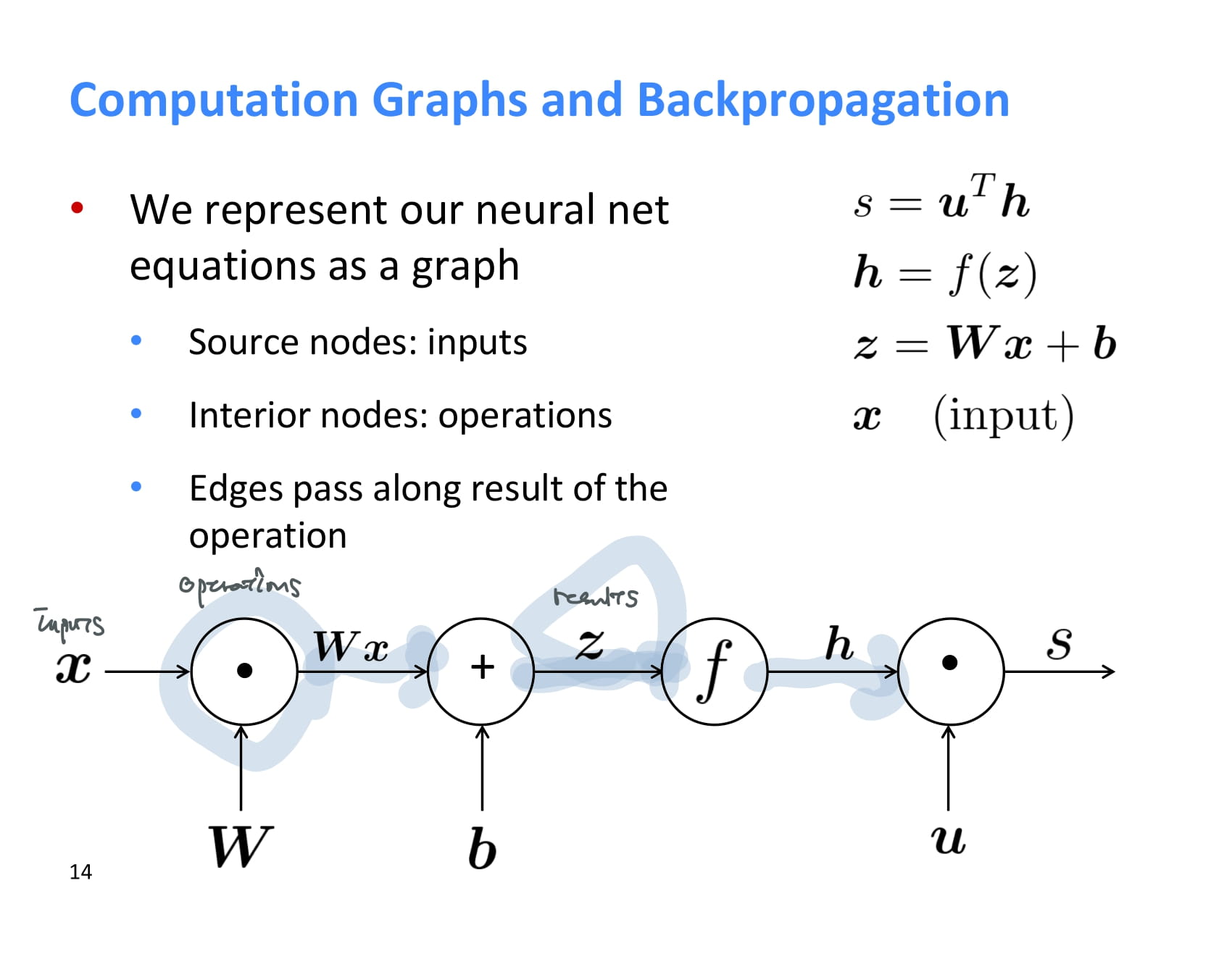
forward propagation이란 순방향 전파를 말하는거였다. 그냥 input에서부터 쭉쭉 계산해주면 된다.

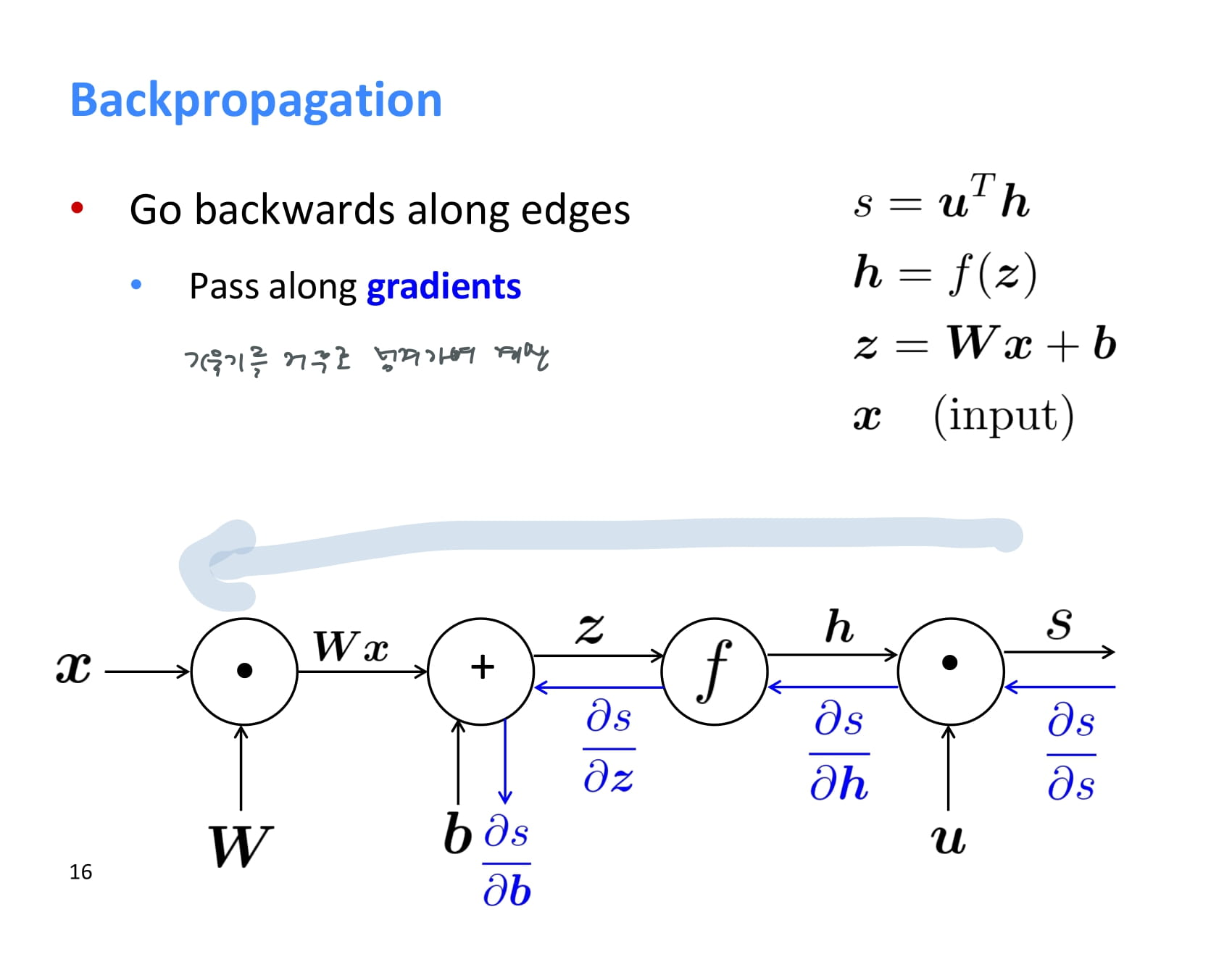
backpropagation은 뒤에서부터 계산된다. 첫번째로 계산되는 기울기 $\partial{s}\over\partial{s}$ 는 무조건 1이다.

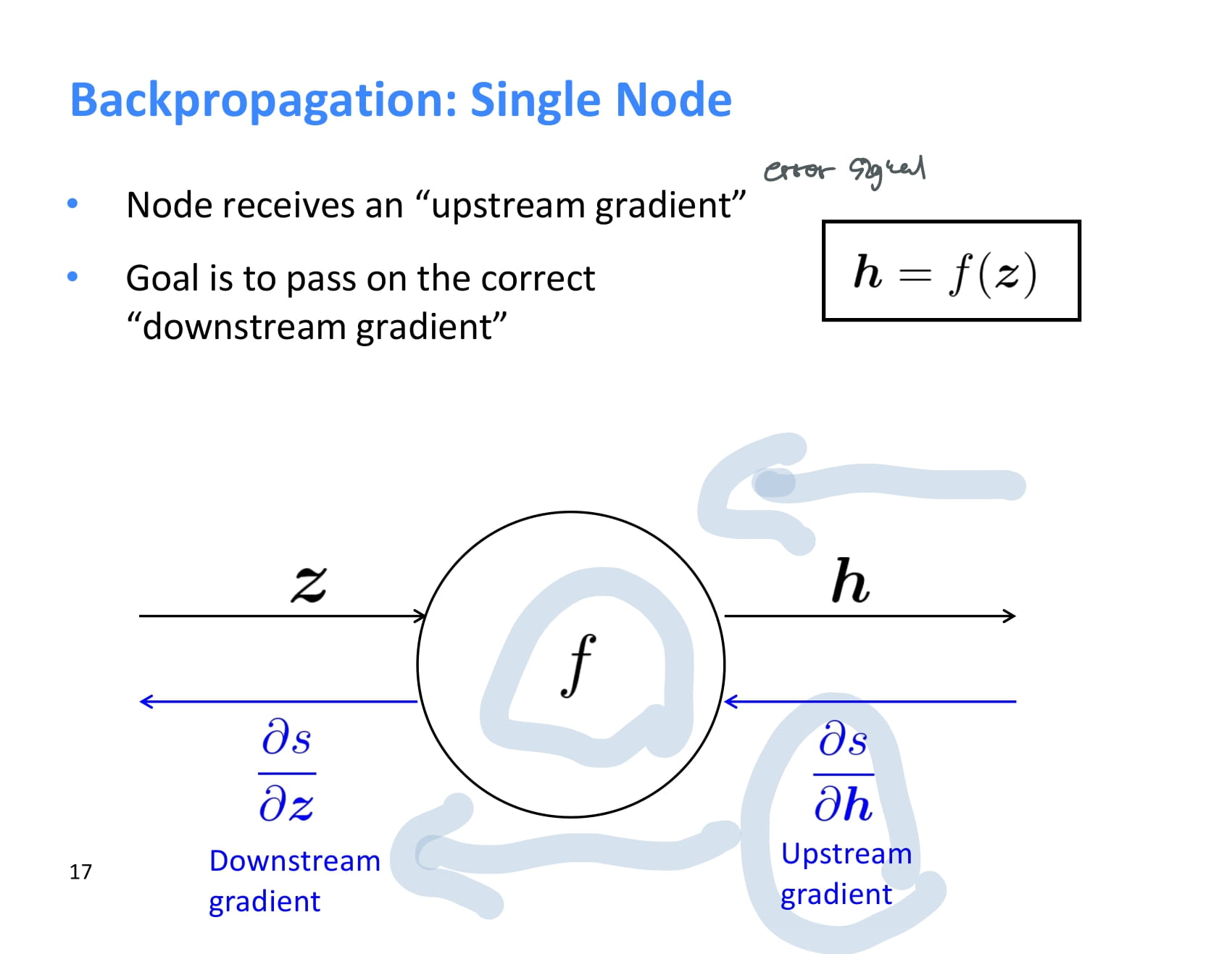
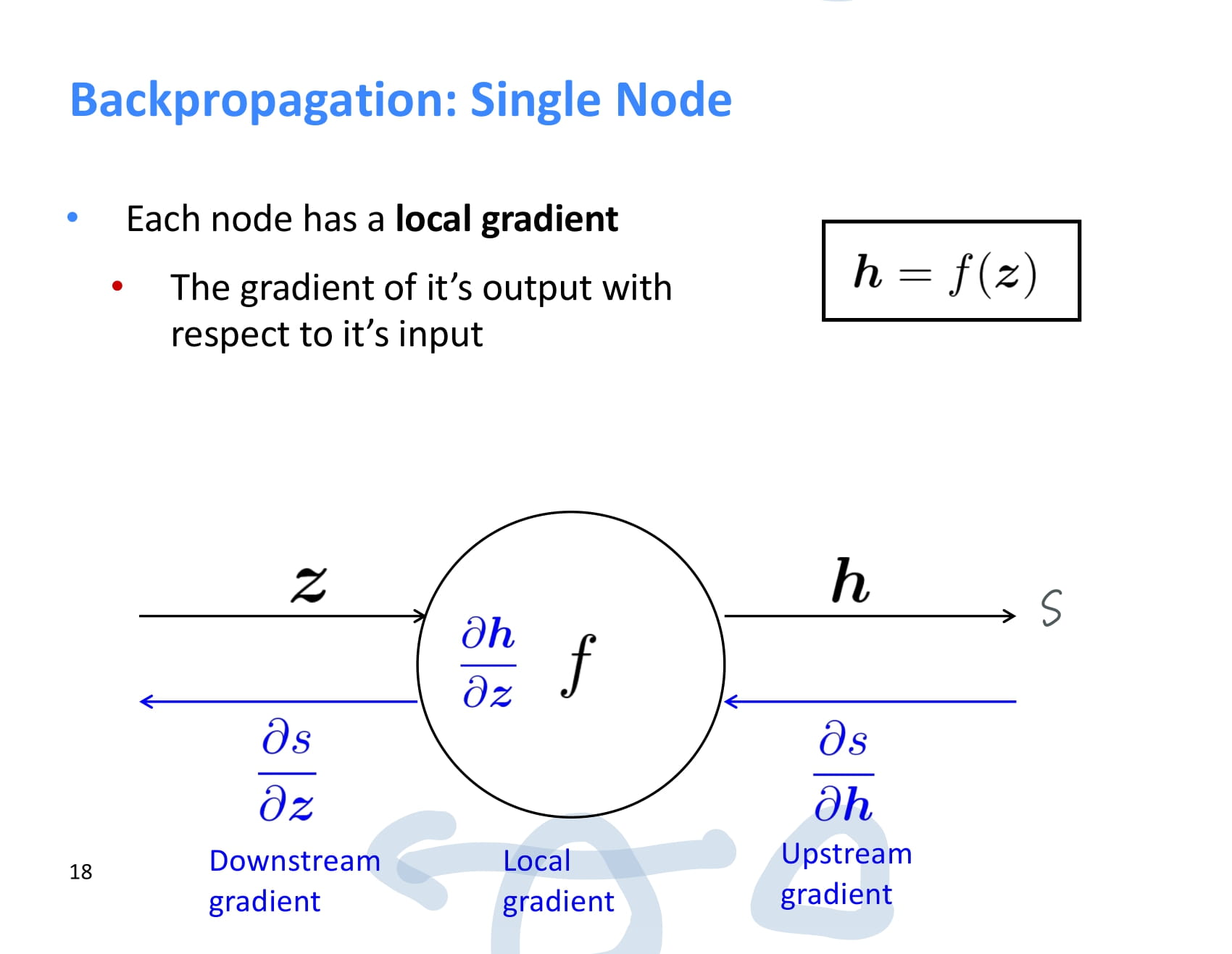
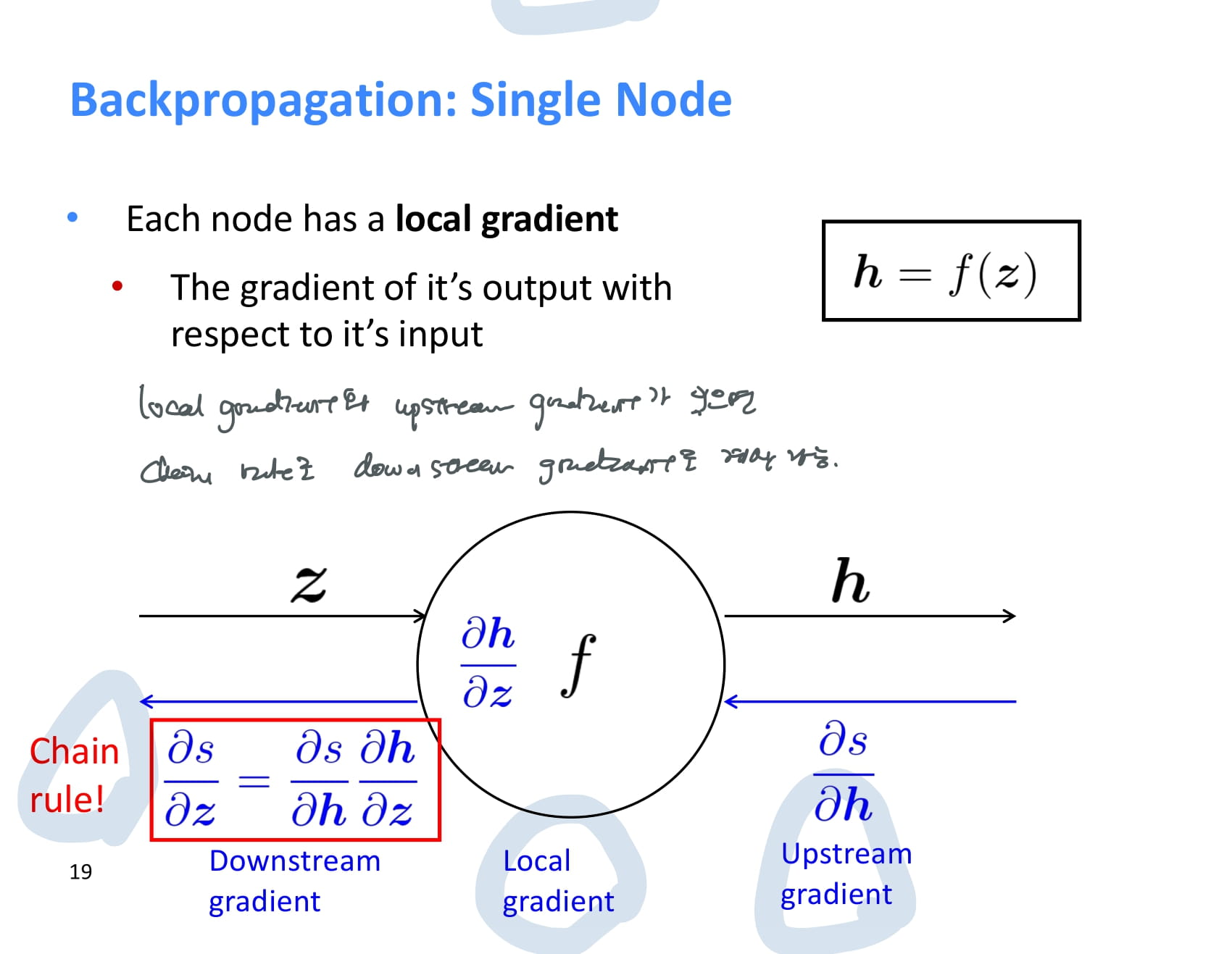
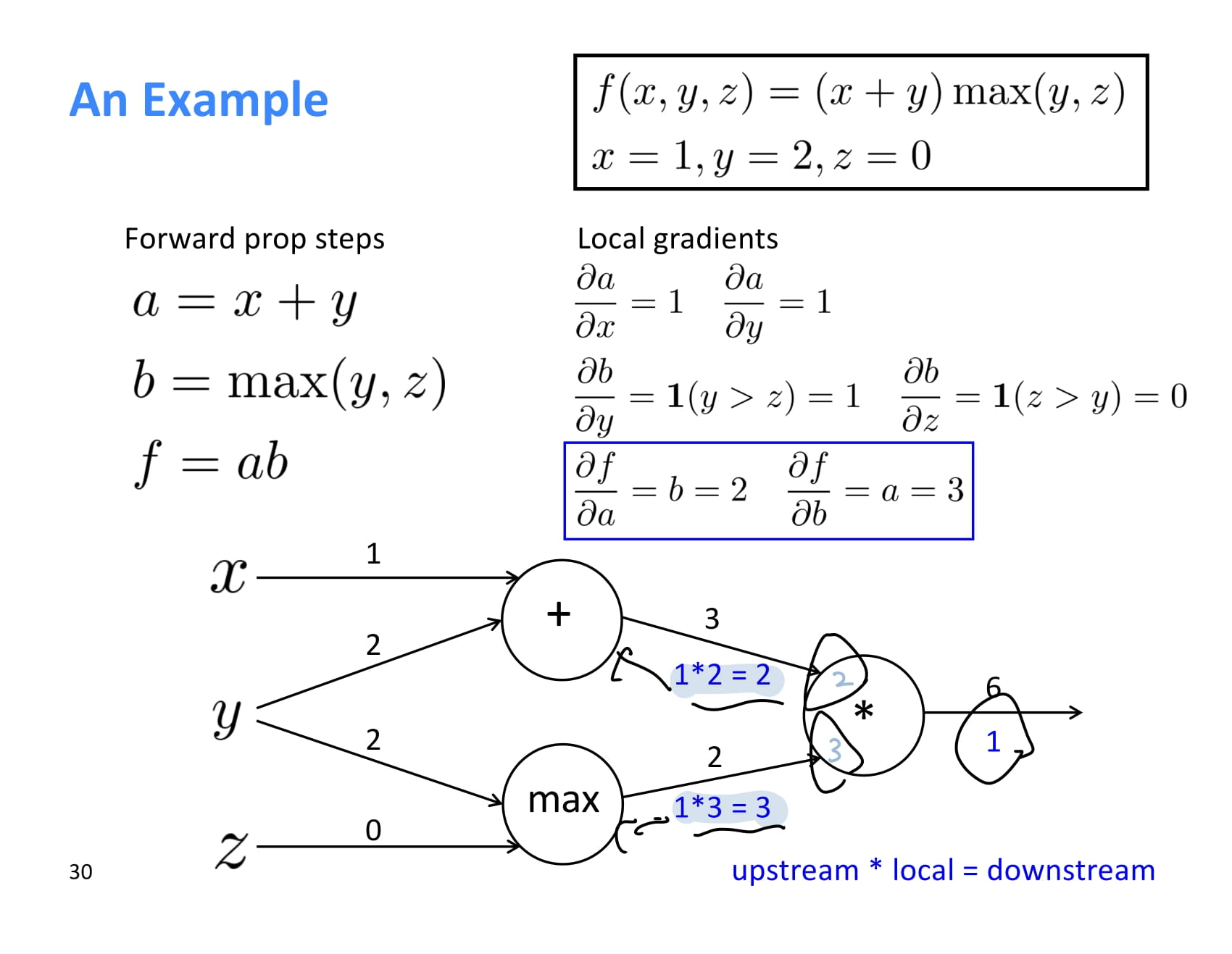
각 node는 backpropagation을 할 때 upstream gradient를 받아 local gradient를 곱한 후 그 결과값을 downstream gradient로 넘겨준다.

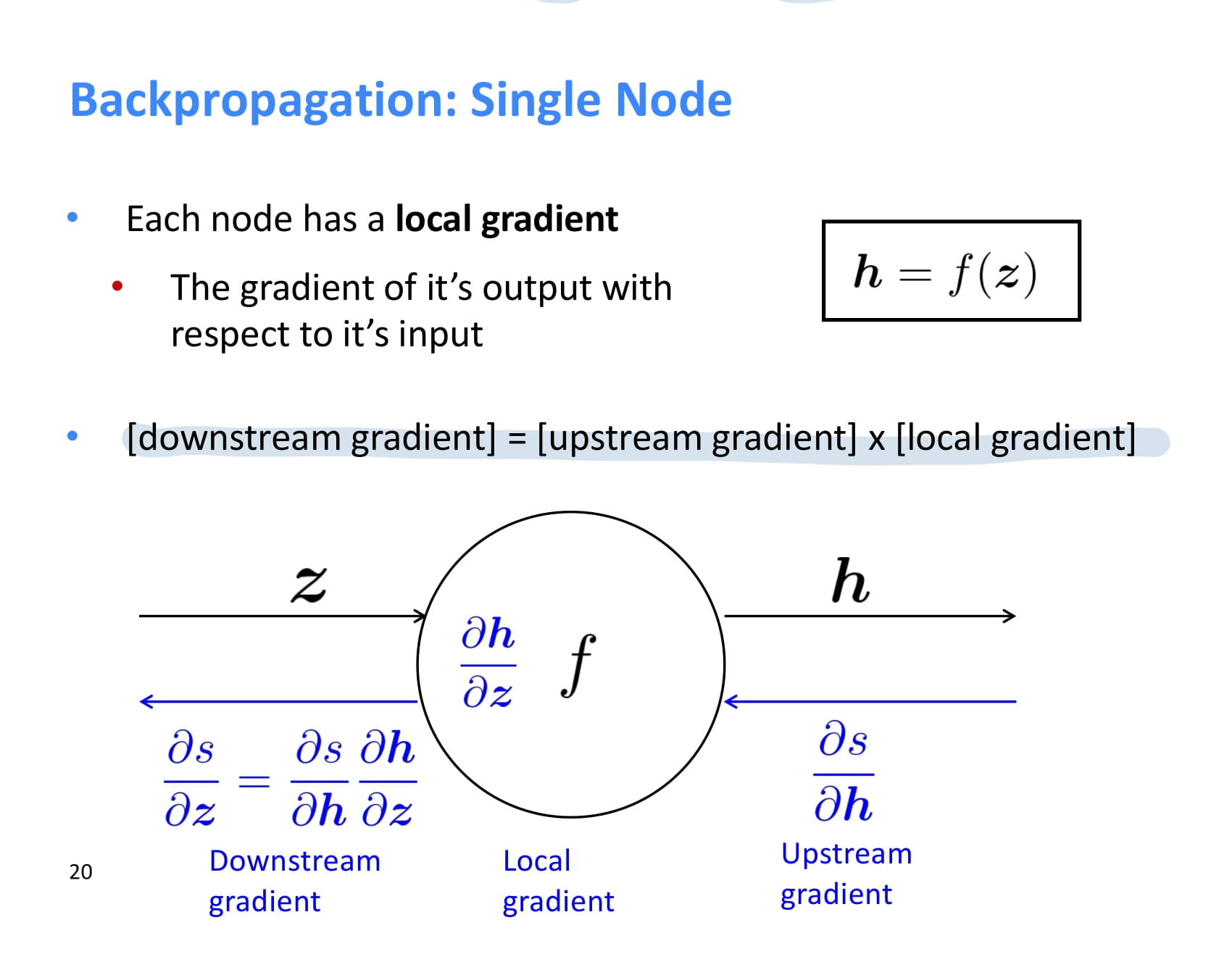
즉 local gradient와 upstream gradient가 있으면 chain rule을 이용해 downstream gradient도 계산할 수 있다.

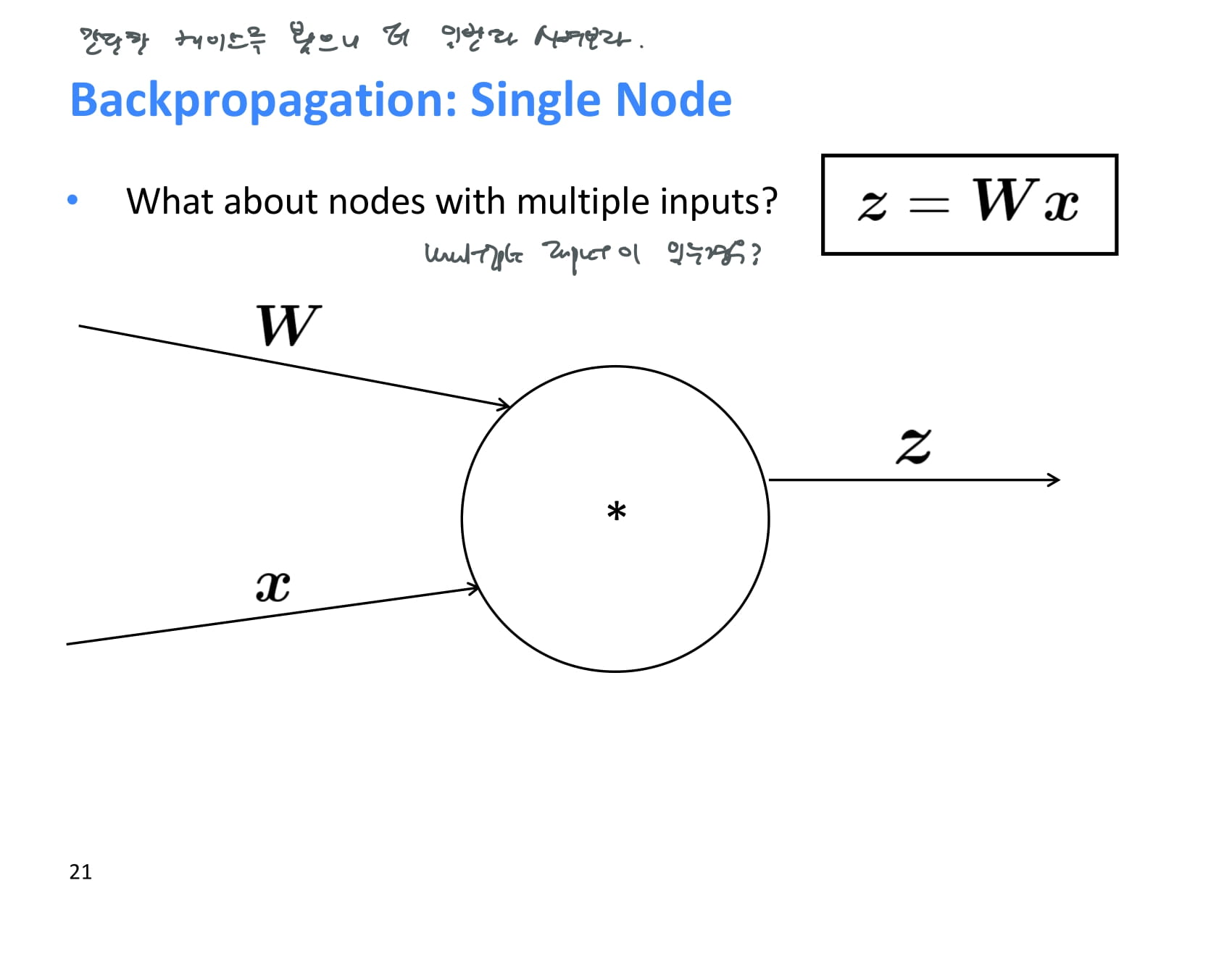
위에서는 간단한 케이스를 봤으니 더 일반화 시켜보자.

한 operation에 여러 input이 존재하는 경우에는 기울기를 어떻게 계산해야할까?

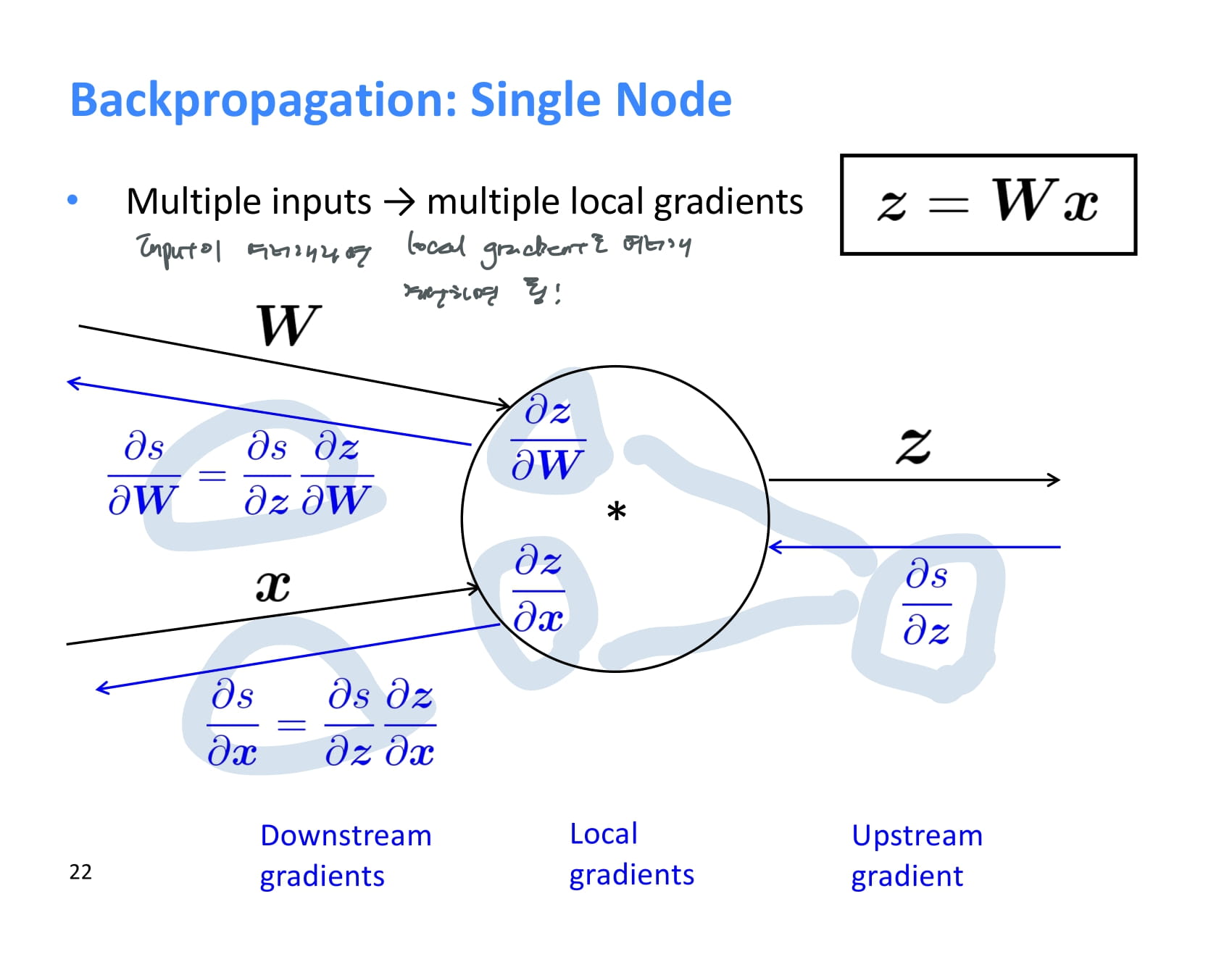
input이 여러개인 경우 local gradient도 여러개를 가지고 downstream gradient를 계산하면 된다!

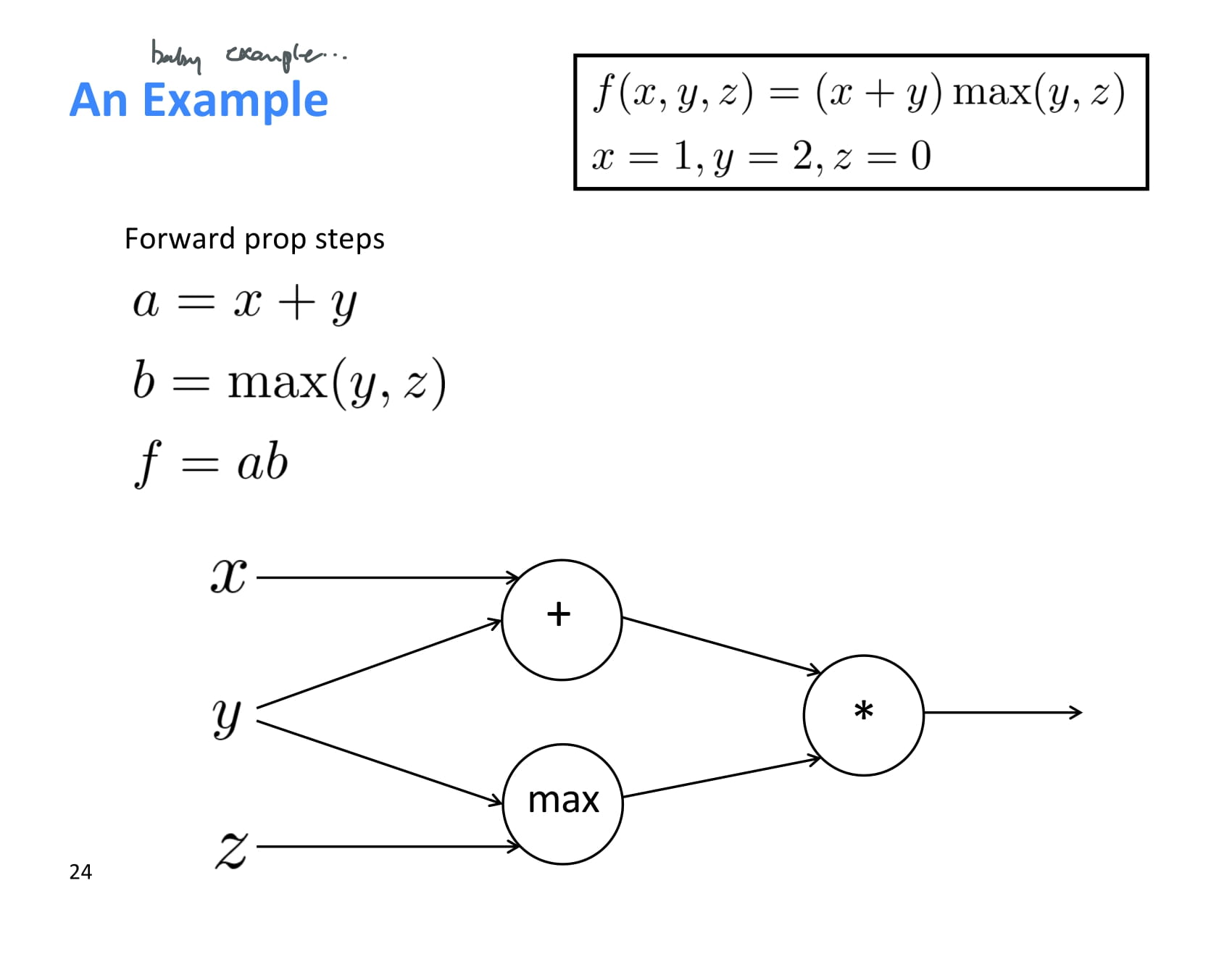
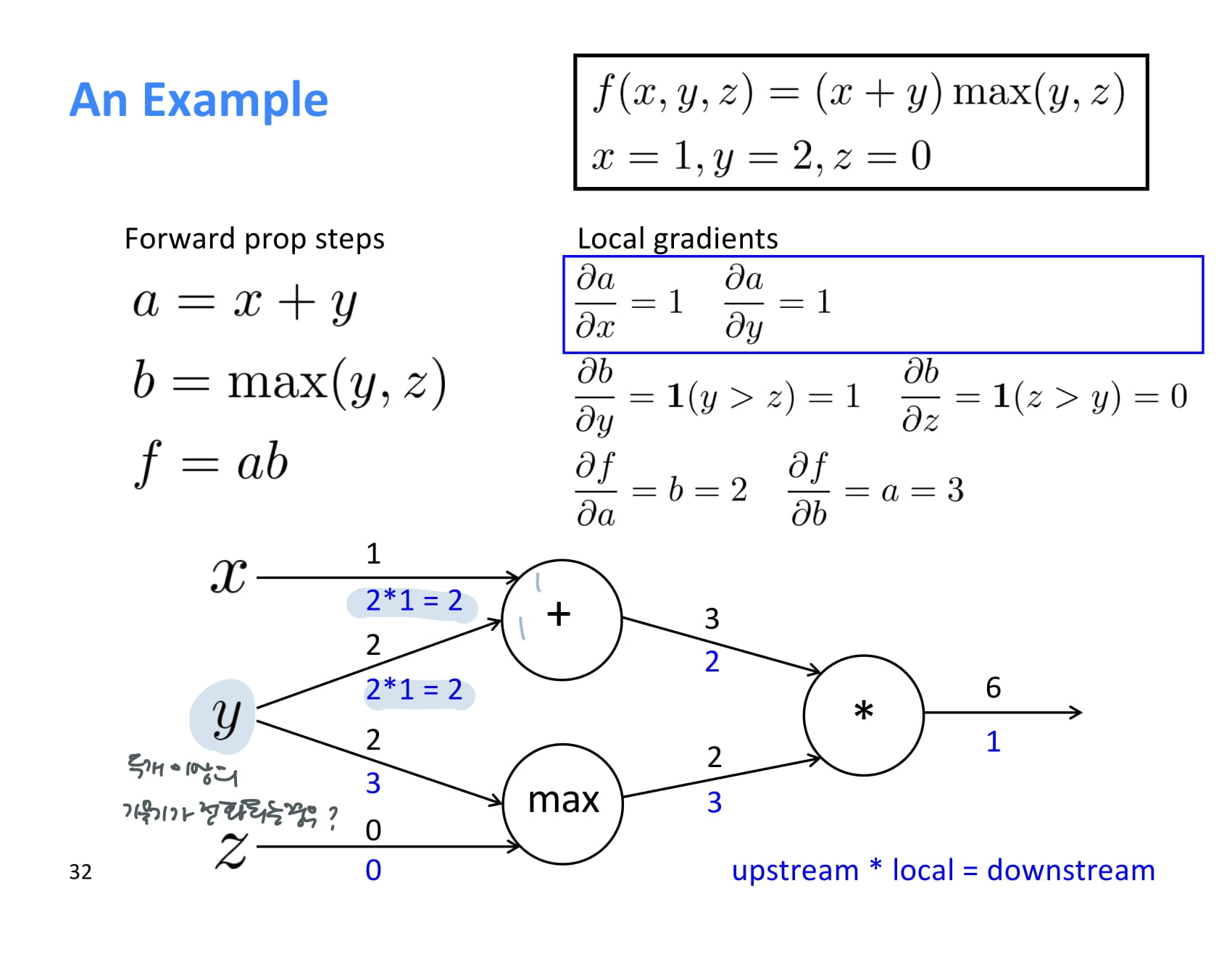
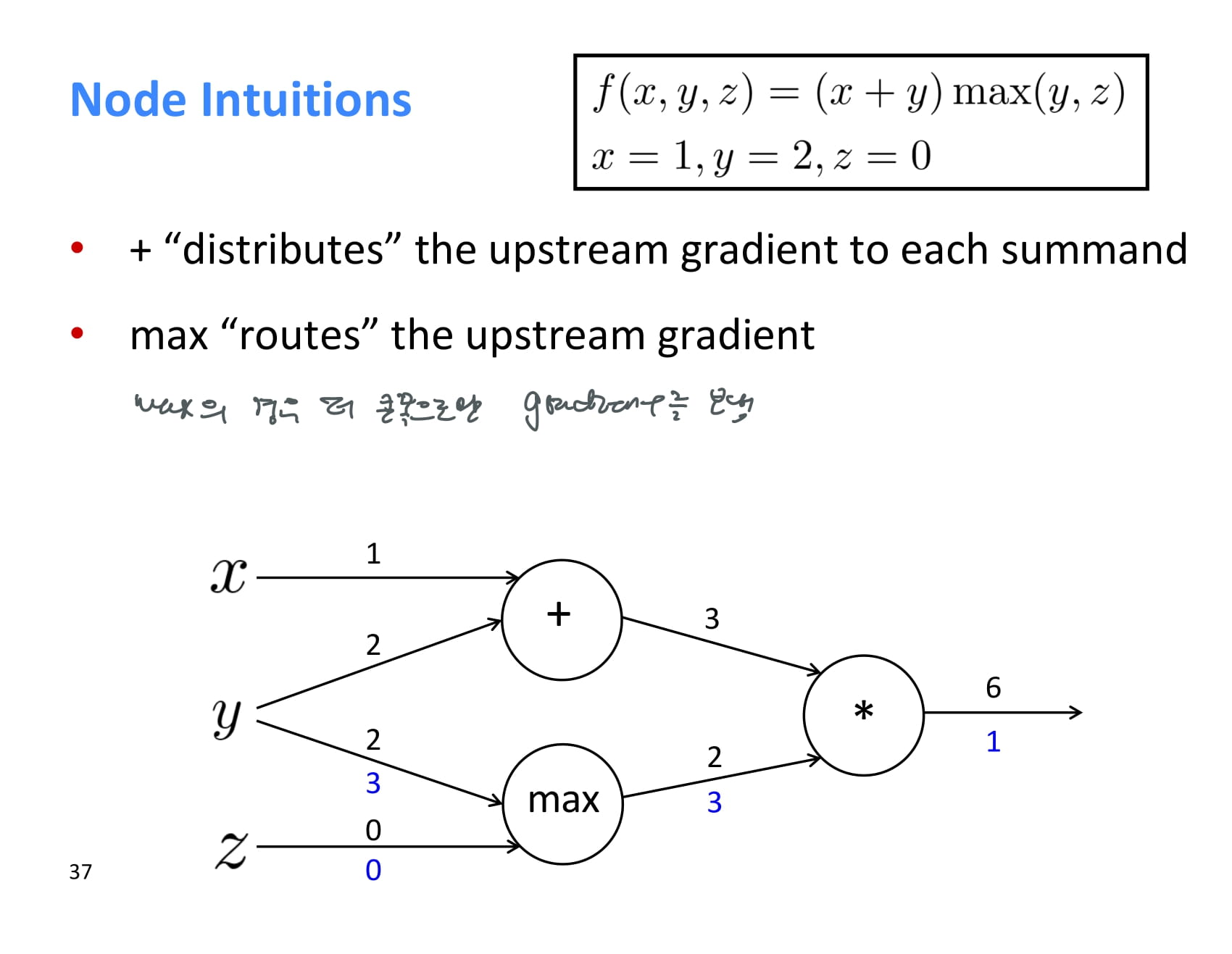
작고 간단한 baby example..

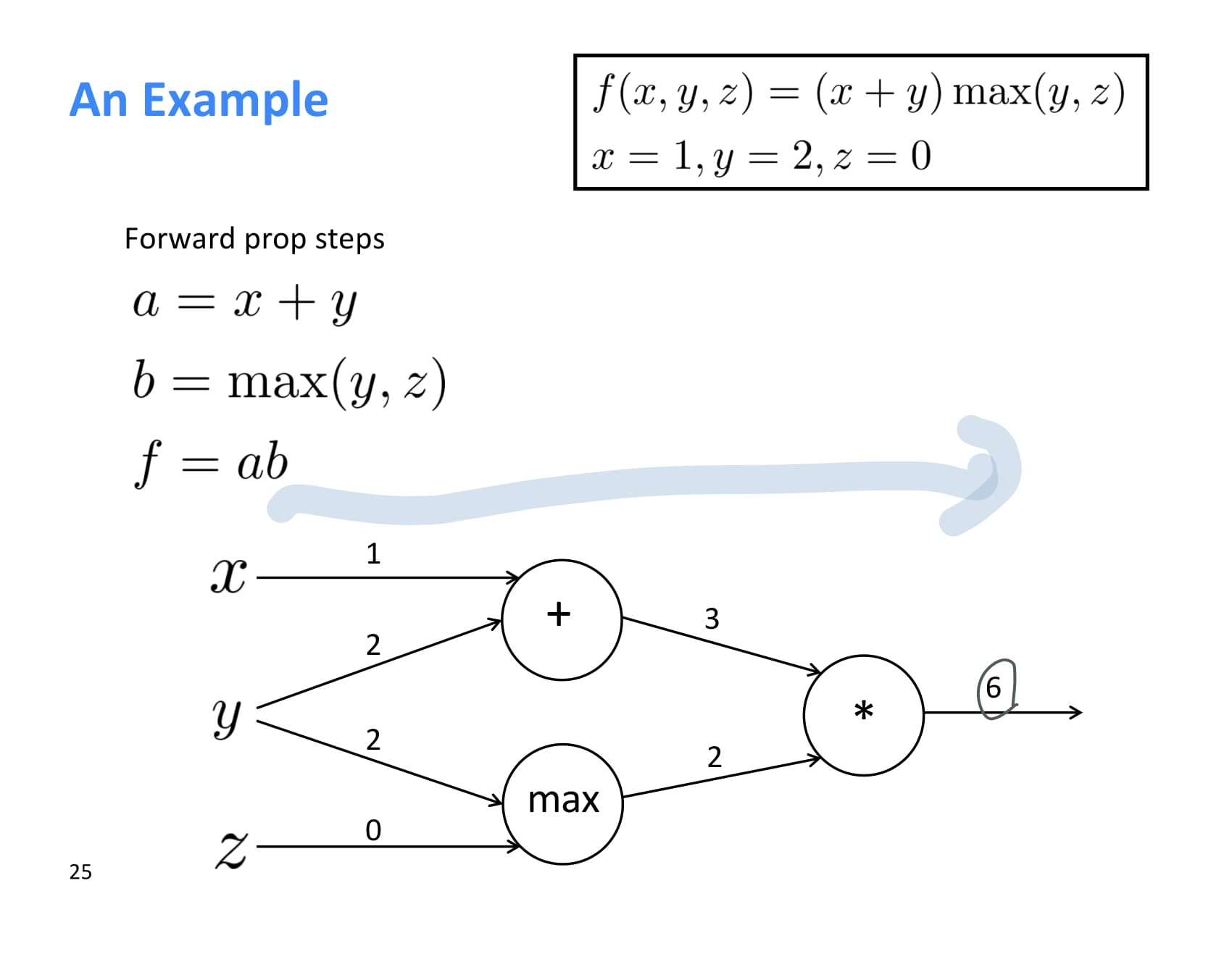
forward propagation 결과는 위 그림과 같다.

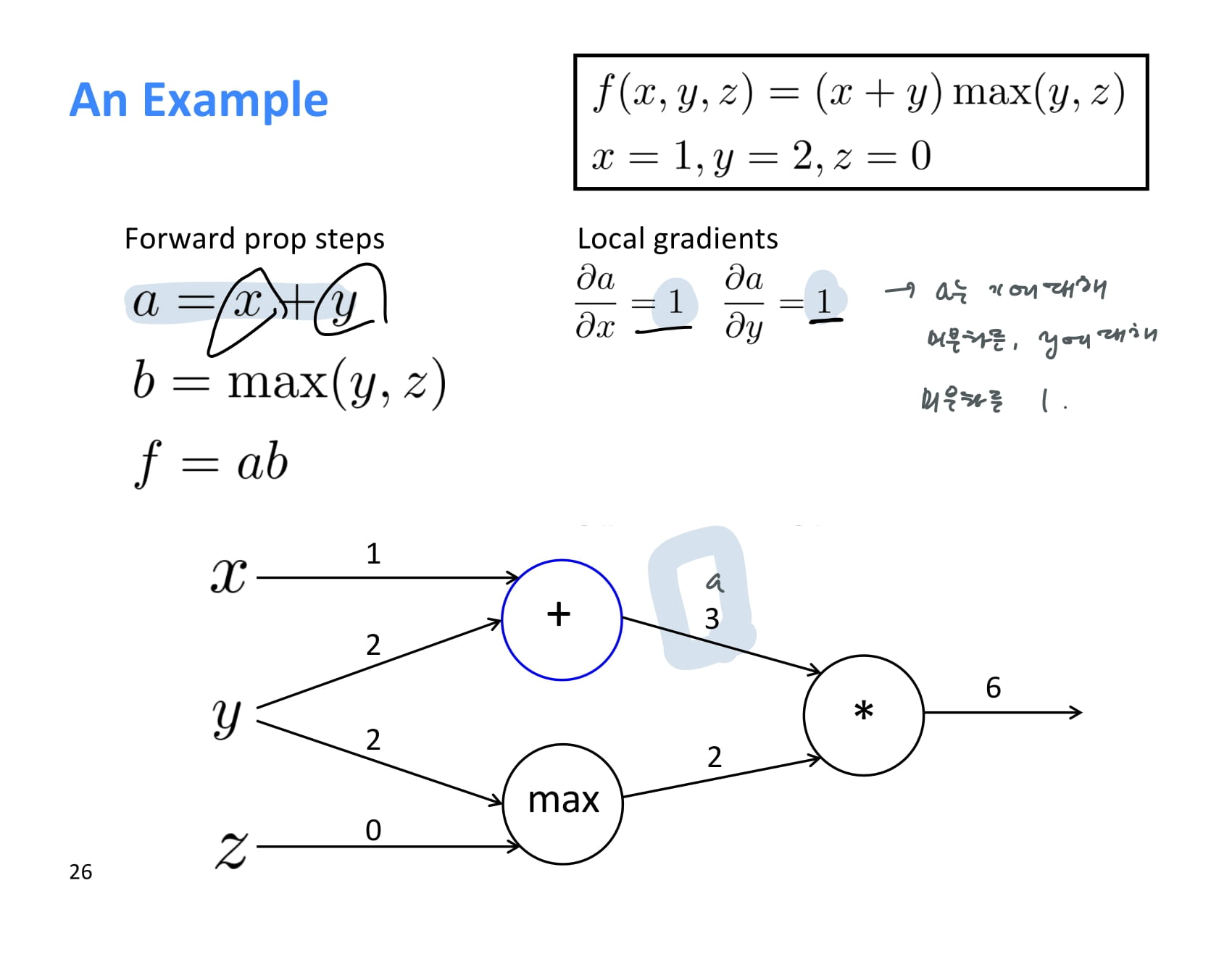
backprop을 해주기 위해 local gradient를 먼저 하나씩 계산해준다.

$\partial{a}\over\partial{x}$ 와 $\partial{a}\over\partial{y}$ 는 모두 1이다.

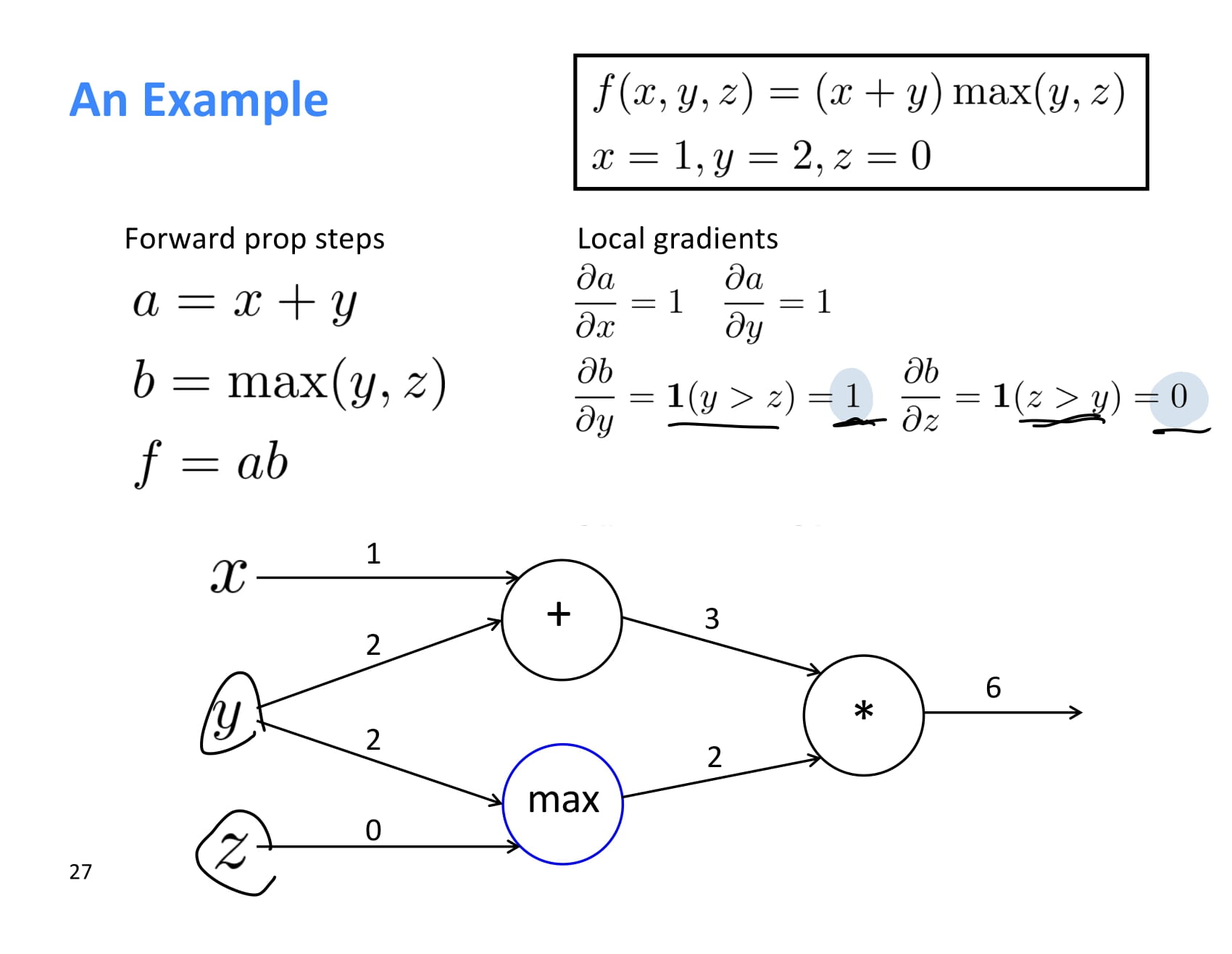
max에서 local gradient를 구하는 것은 더 어려워보일 수 있지만 쉽다.

$\partial{b}\over\partial{y}$ 는 y > z인 경우 1이고, $\partial{b}\over\partial{z}$ 는 z > y 인 경우 1이다.

따라서 $\partial{b}\over\partial{y}$ 는 1, $\partial{b}\over\partial{z}$ 는 0이다.

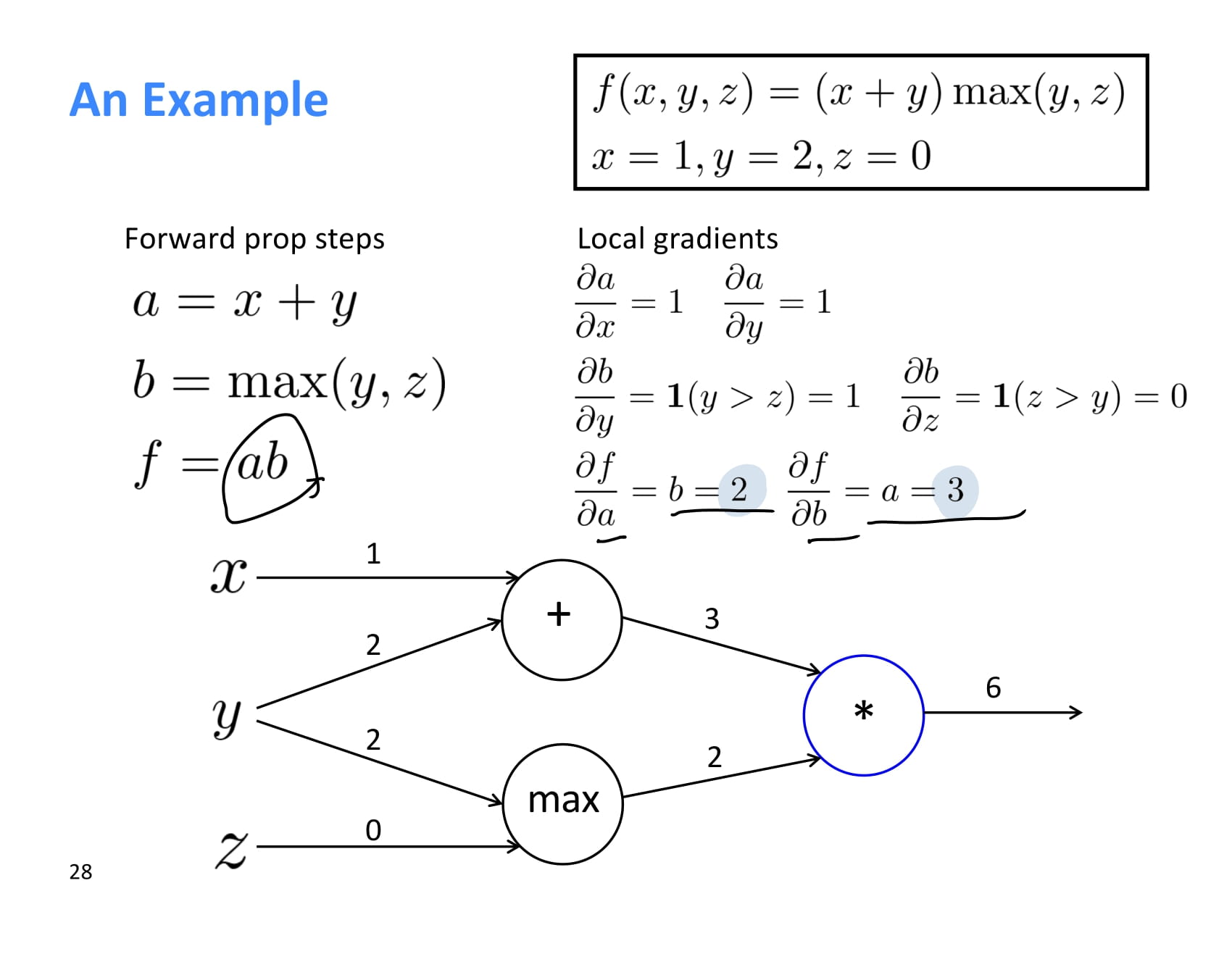
곱셈의 미분도 어렵지 않다.

$\partial{f}\over\partial{a}$ 는 $b$ 이므로 2, $\partial{f}\over\partial{b}$ 는 $a$ 이므로 3이다.

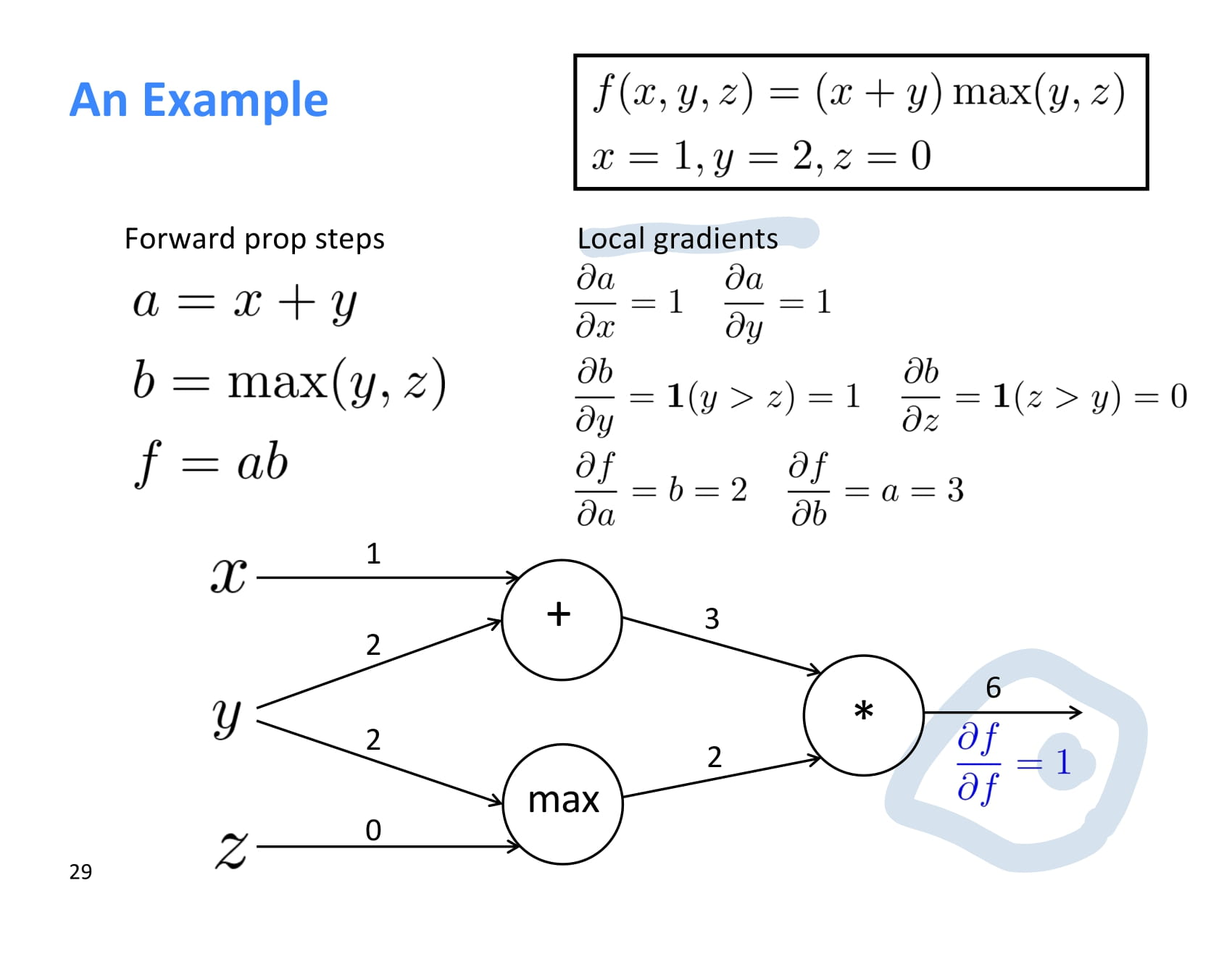
이제 최초 기울기 ${\partial{f}\over\partial{f}} = 1$ 에서 시작해 upstream gradient를 각 local gradient와 쭉쭉 곱해나가면 된다.

계산 과정은 쉬우니 설명은 생략.

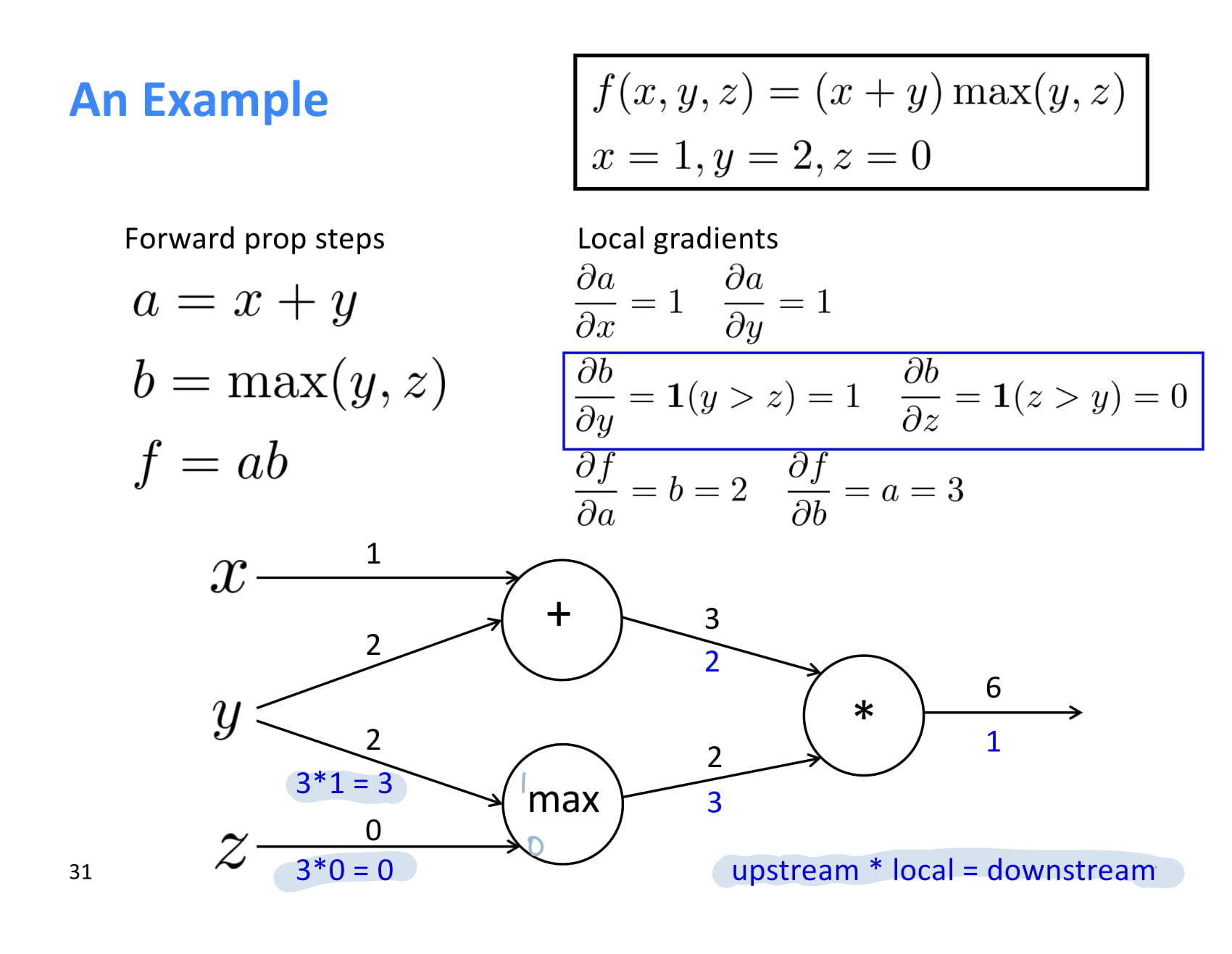
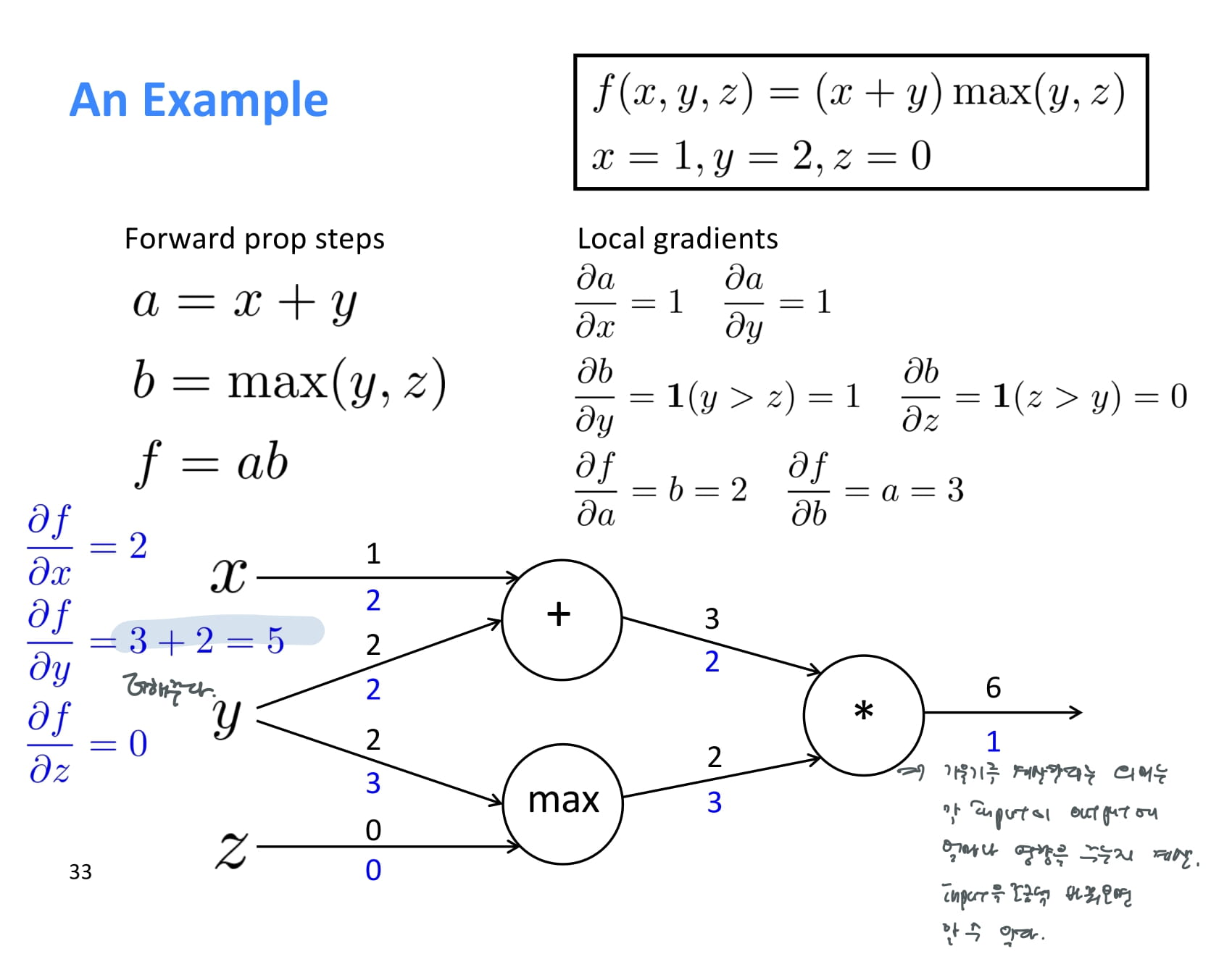
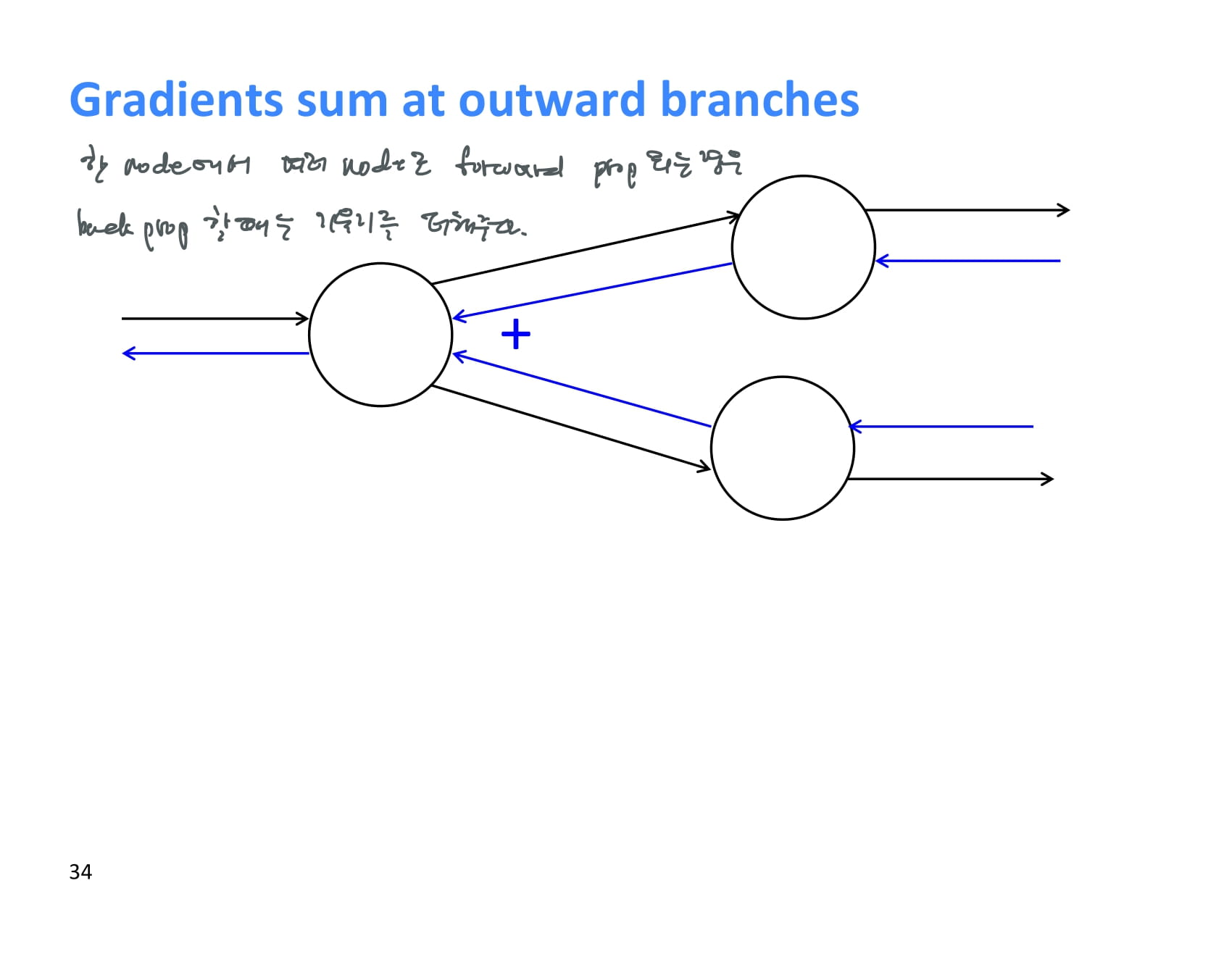
한 node에서 여러 node로 forward propagation이 일어나는 경우, backpropagation 할때에는 upstream gradient 두 개를 더해주면 된다.

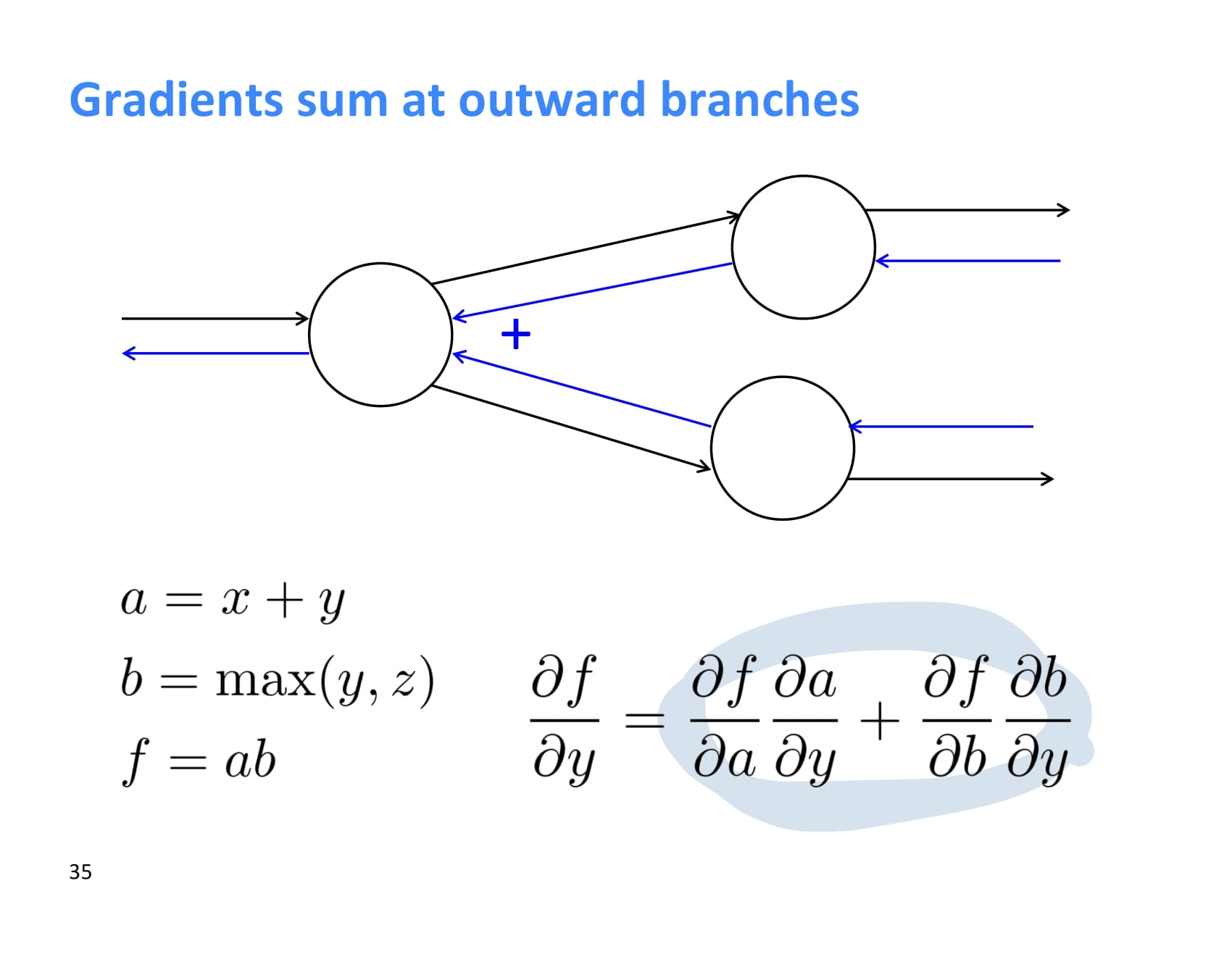
조금 더 직관적으로 operation 별 역전파의 특징을 이해해보자.

+ operation에서 역전파하는 경우, upstream gradient가 그대로 downstream에 복사된다.

max의 경우 더 큰 쪽으로만 gradient를 보내준다.

더 큰 쪽에서만 max의 결과값이 영향을 받기 때문에 당연한 소리다.

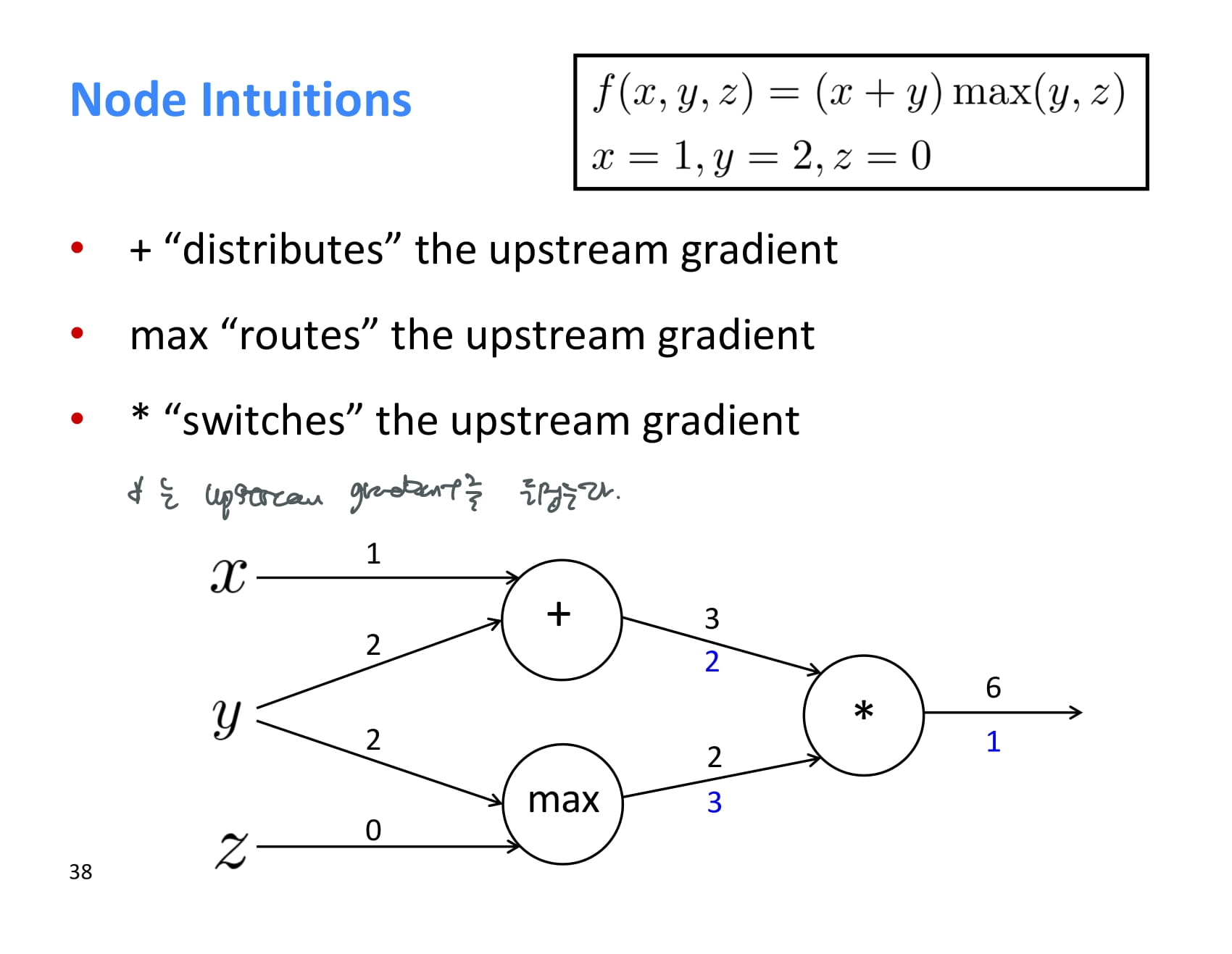
* 는 forward propagation 시 온 값을 서로 바꿔서 돌려보내준다.

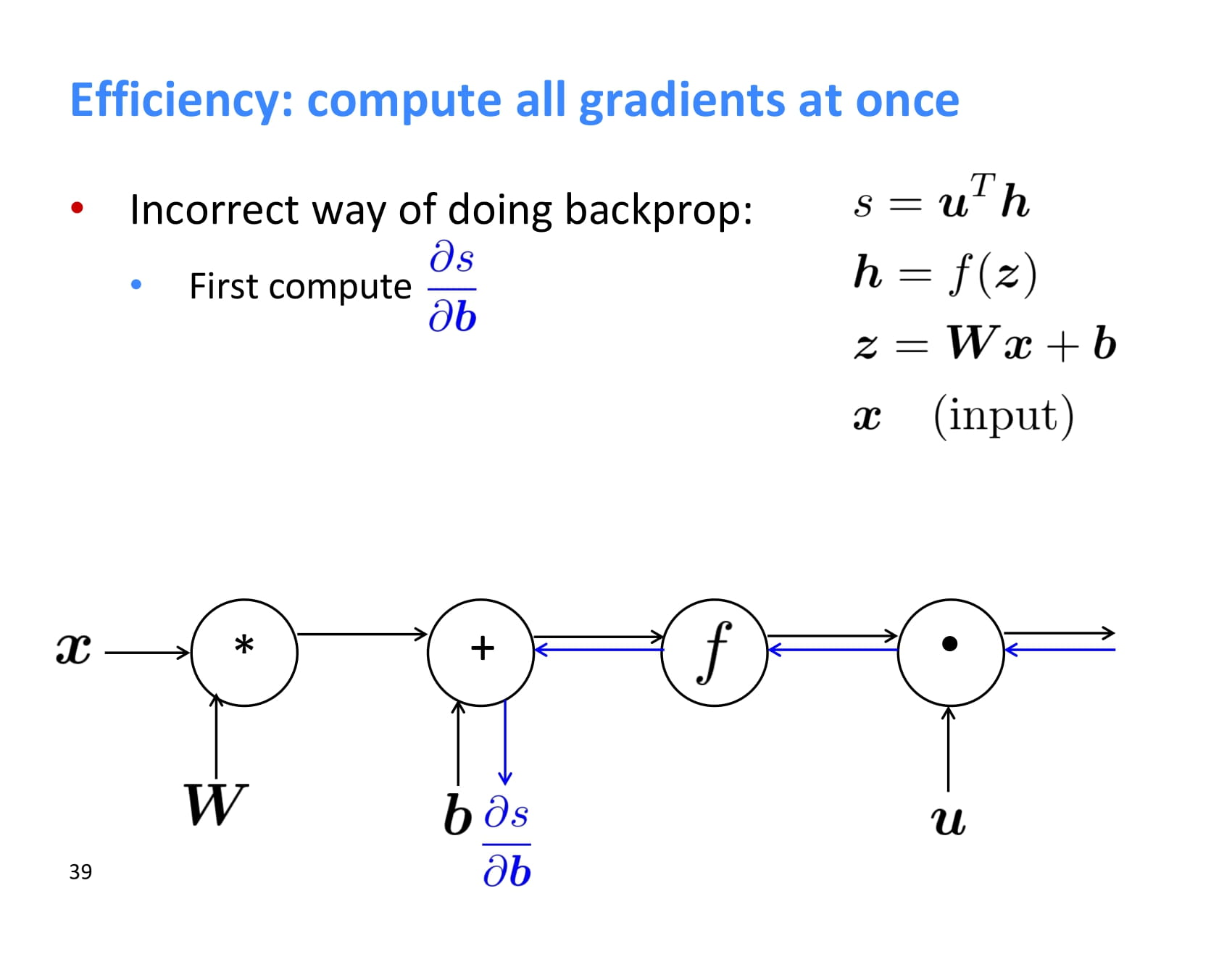
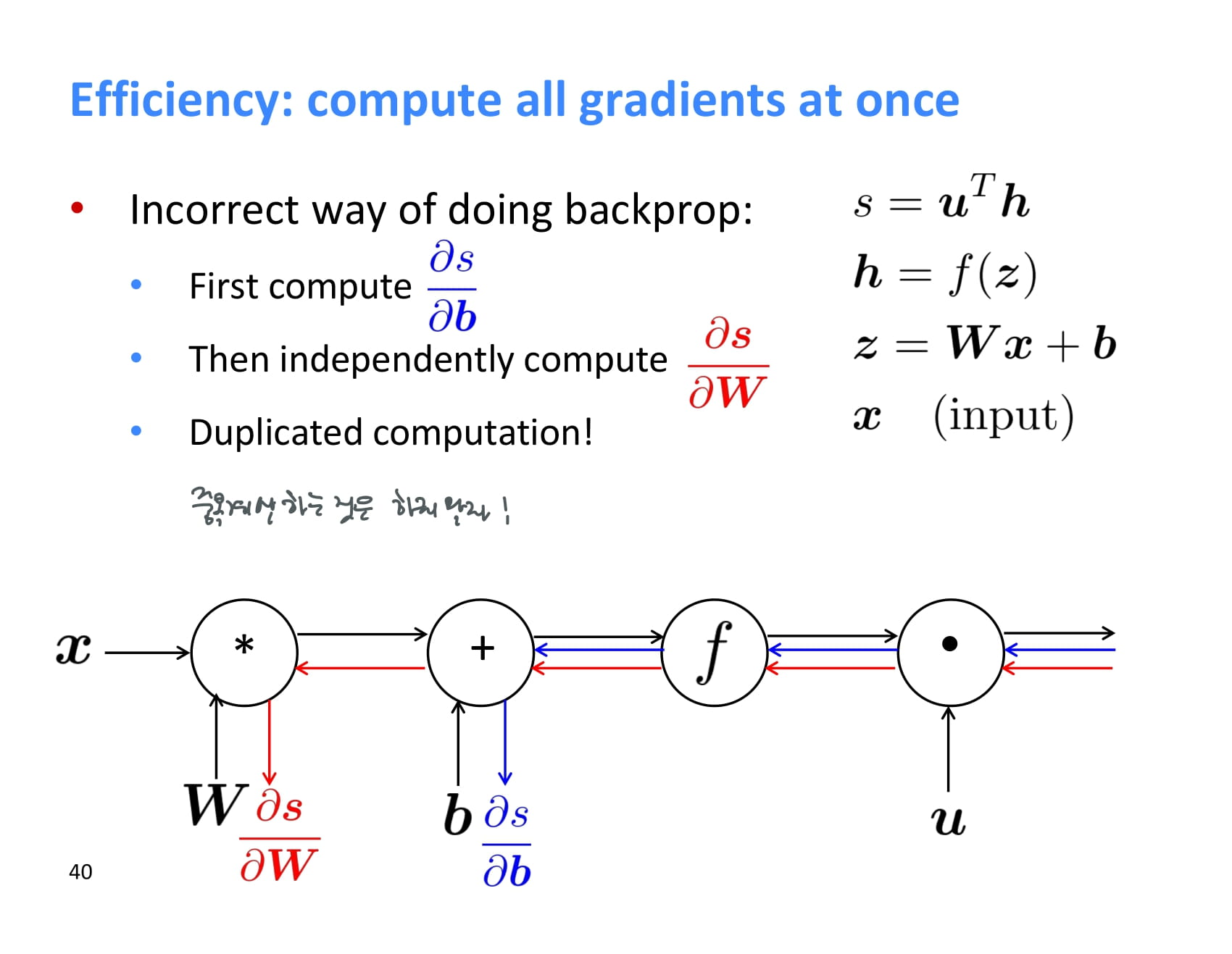
이렇게 backpropagation을 하다보면 결과값과 가까운 upstream gradient들은 계속해서 계산하게 되는데, 반복 계산하지 말고 어디 저장해두는 것이 좋다.

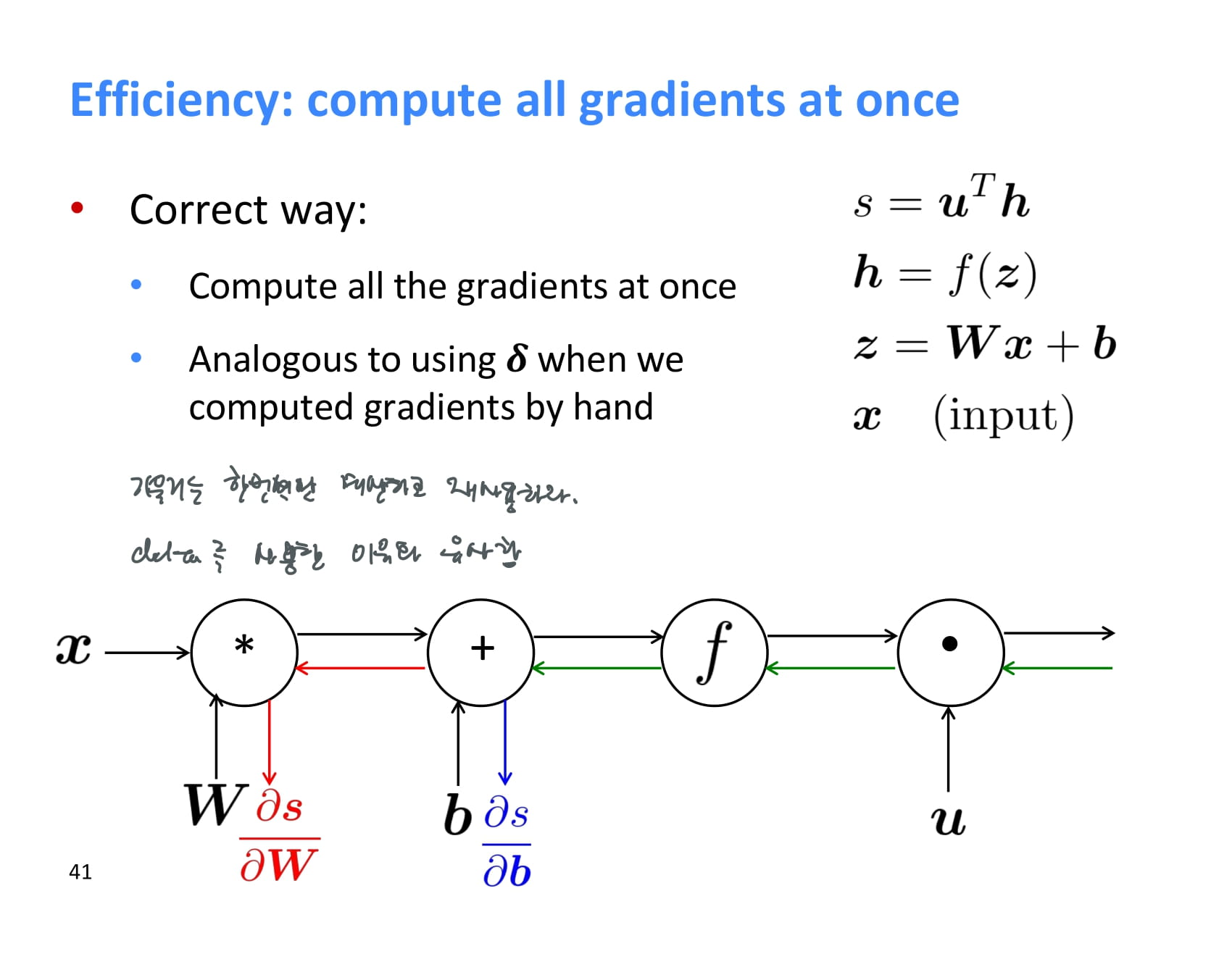
이런 backpropagation은 보통 acyclic graph에 대해 수행되고, 이상하게 구현하지 않았다면 forward propagation과 backpropagation의 시간복잡도는 같다.

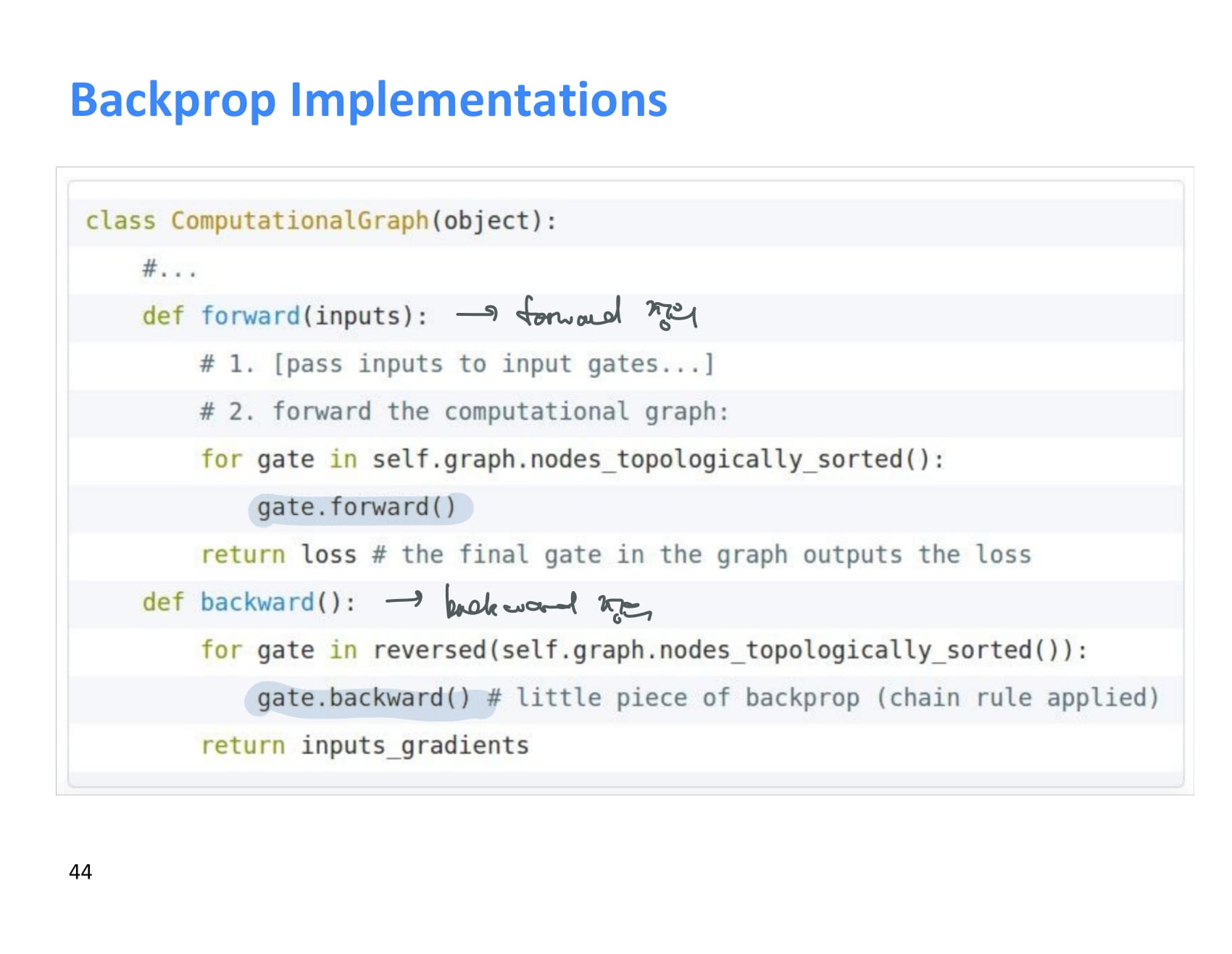
현대의 deep learning framework에서는 backward와 forward를 어떻게 할지 이런식으로 정해주면 된다. 거의 이미 구현된 것을 사용할 것 같긴 하지만..

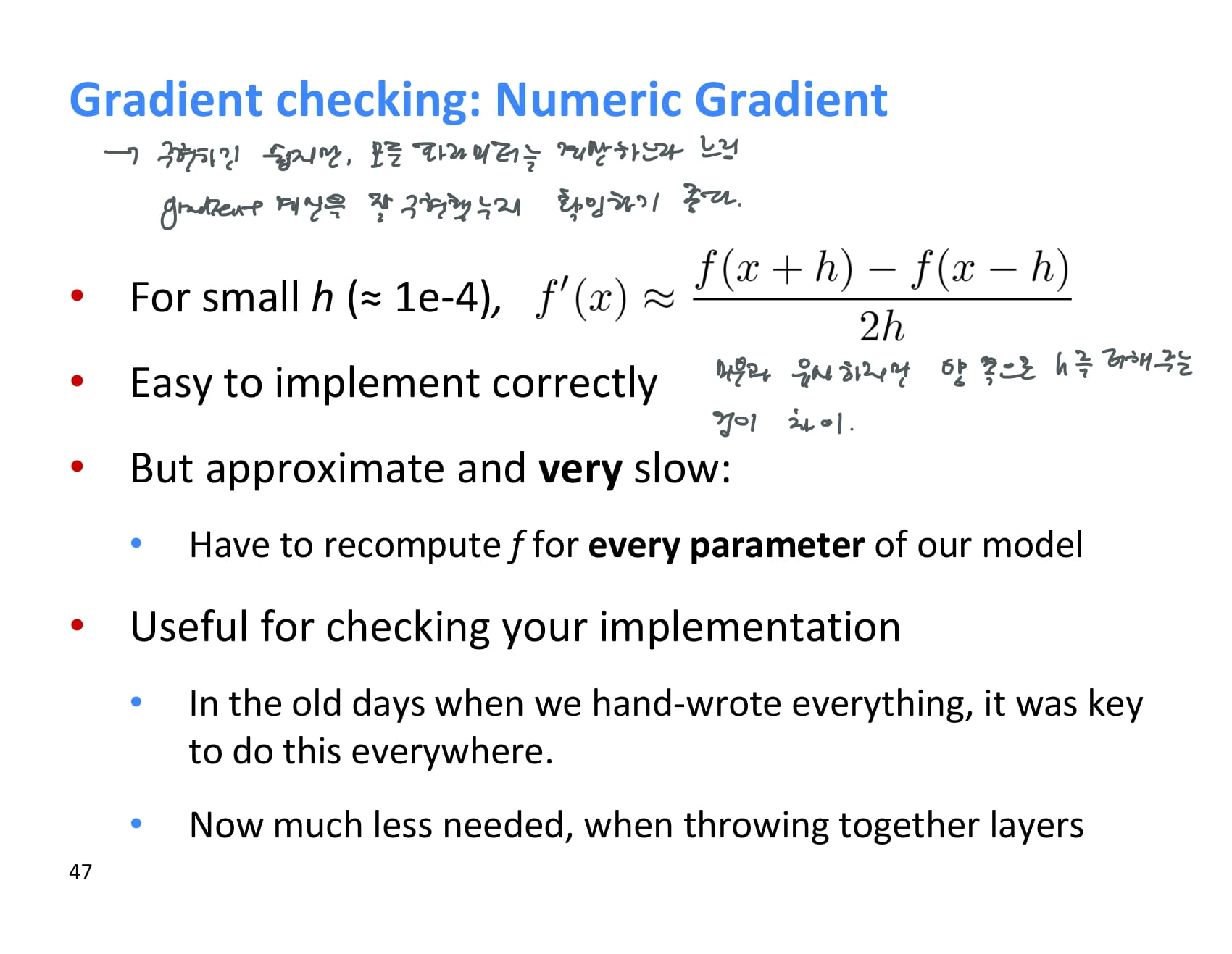
numeric gradient라는 것도 존재한다.

$f^\prime(x)\approx{f(x+h)-f(x-h)\over{2h}}$

미분과 유사하지만 x의 양방향으로 아주 작은 h를 더하고 빼주는 것이 차이이다.

구현하기도 쉽고 더 정확하지만 계산량이 더 많기 때문에 느릴 수 있다.

따라서 numeric gradient는 기울기를 잘 계산하고 있는지 체크할 때 사용하기 좋다.

neural net의 핵심 기술을 마스터했따!

힘든 여정이었다.

왜 이런것까지 알아야 하나요? tmi 아닌가요?

현대의 멋진 딥러닝 프레임워크들이 이런것을 모두 구현해놨고 매커니즘을 몰라도 잘 동작한다.

하지만 문제가 생겼을 때 디버깅하고 개선하기 위해서는 이런 원리를 알아야 한다.

이제 핵심 기술들은 마스터했으니 주변 기술들을 알아보자.

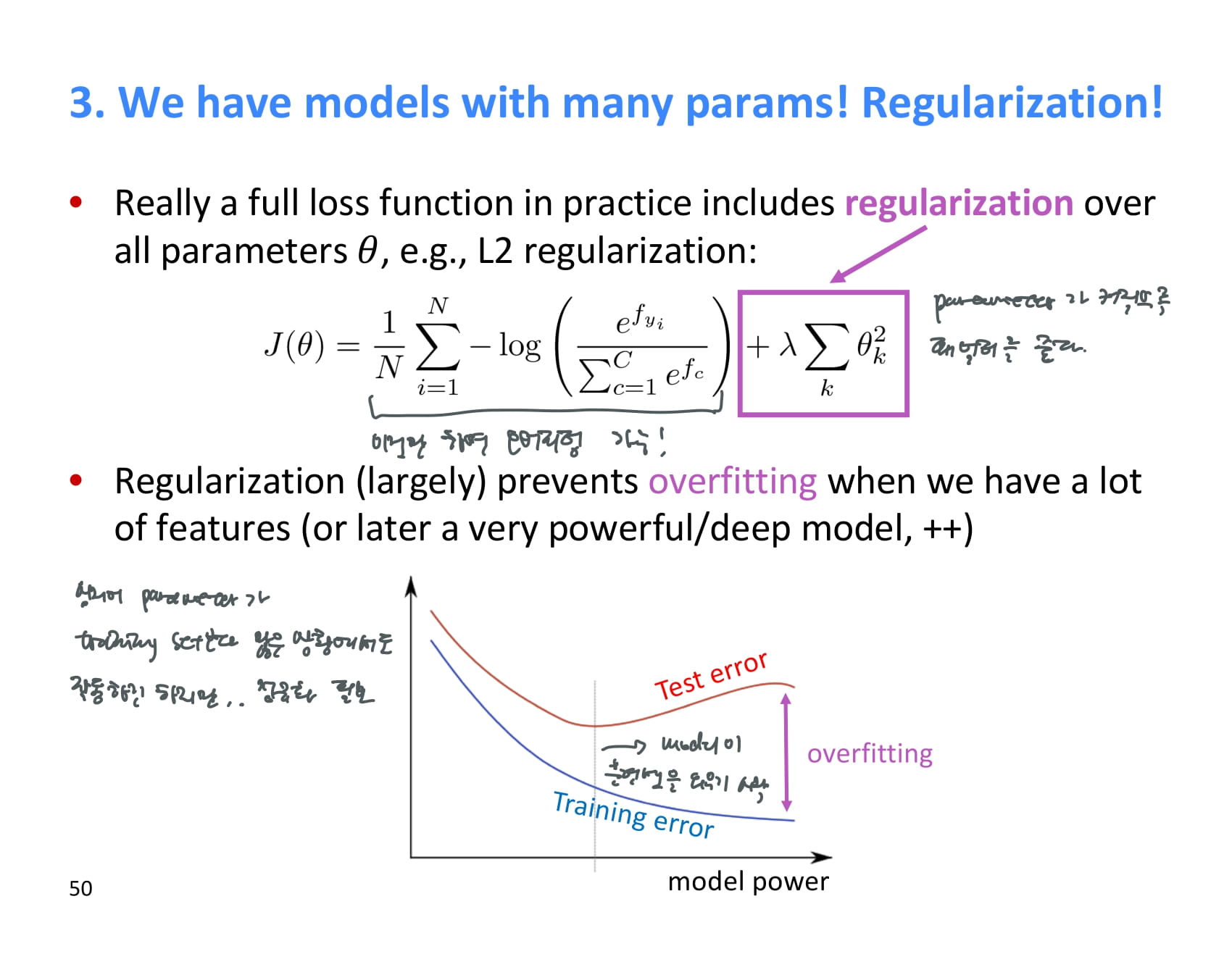
실제로 쓰이는 loss function에는 보통 regularization 해주는 항이 존재한다.

대표적으로는 L2 regularization이 있는데, 이것은 parameter가 커질수록 패널티를 주어 오버피팅을 방지한다.

벡터 연산을 할 때에는 리스트 루프를 도는 것보다 numpy 등을 이용해 매트릭스에 때려넣고 한방에 계산하는게 훨씬 빠르다.

우리가 다룰 데이터는 정말정말 많기 때문에, 훈련이 되는것도 중요하지만 얼마나 빠르게 훈련되는지도 중요하다.

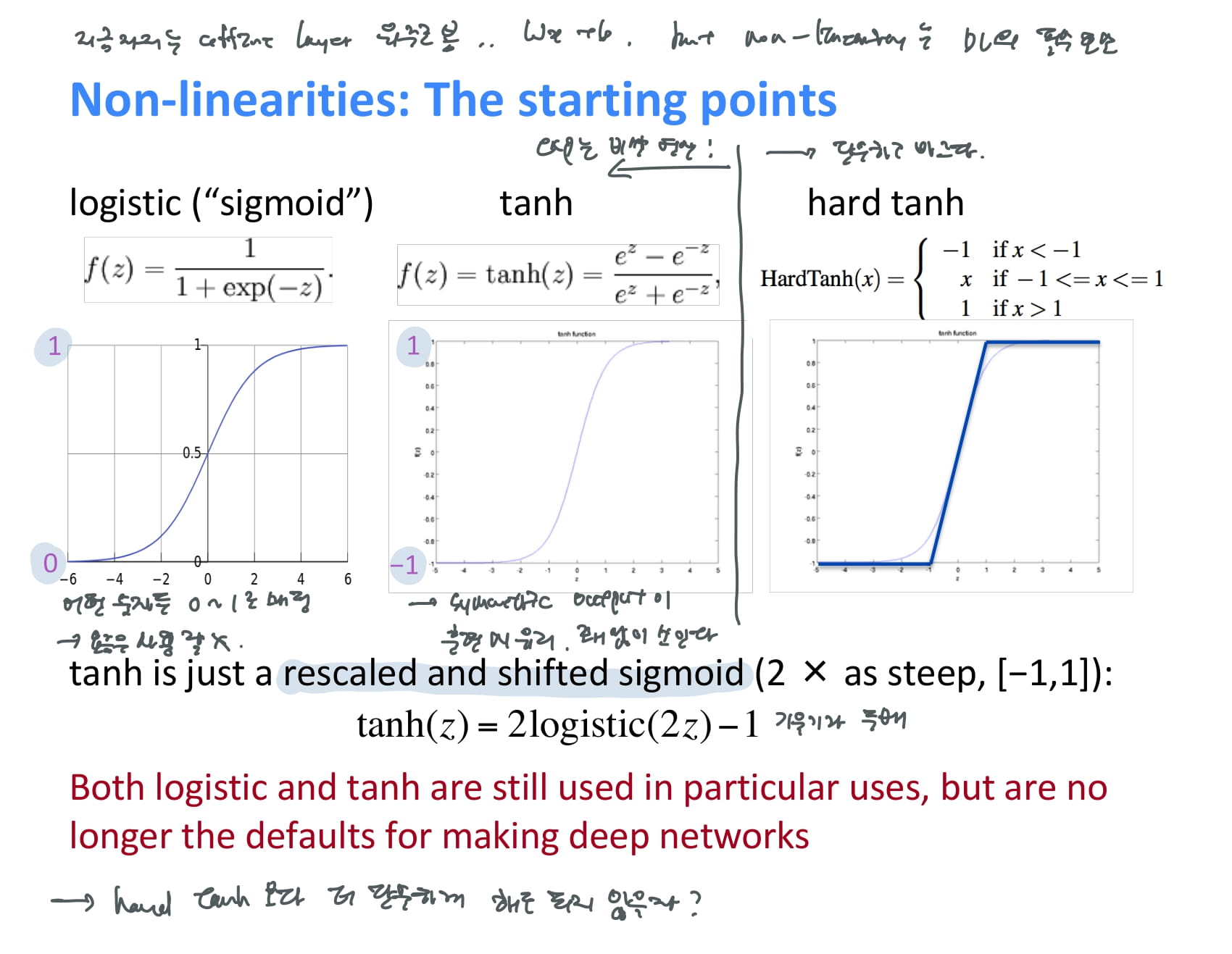
아직 non-linearity에 대한 설명은 자세히 하지 않았지만, non-linearity는 딥러닝과 기존 머신러닝 알고리즘을 구분짓는 딥러닝의 필수요소이다.

대표적인 non-linearity function에는 다음과 같은 것들이 있다.

• sigmoid

  앞에서 자주 본 함수. 어떤 숫자든 0~1로 매핑해준다.

• tanh

  sigmoid와 비슷하지만 -1~1사이로 매핑해준다. symmetric output이라서 훈련 시 유리하다는 교수님 설명.

• hard tanh

  sigmoid와 tanh는 exponential 계산이 너무 비싸서 단순한 hard tanh를 적용했는데, 성능이 생각보다 잘 나왔다. 그러면 이것보다 더 단순해도 되지 않을까?

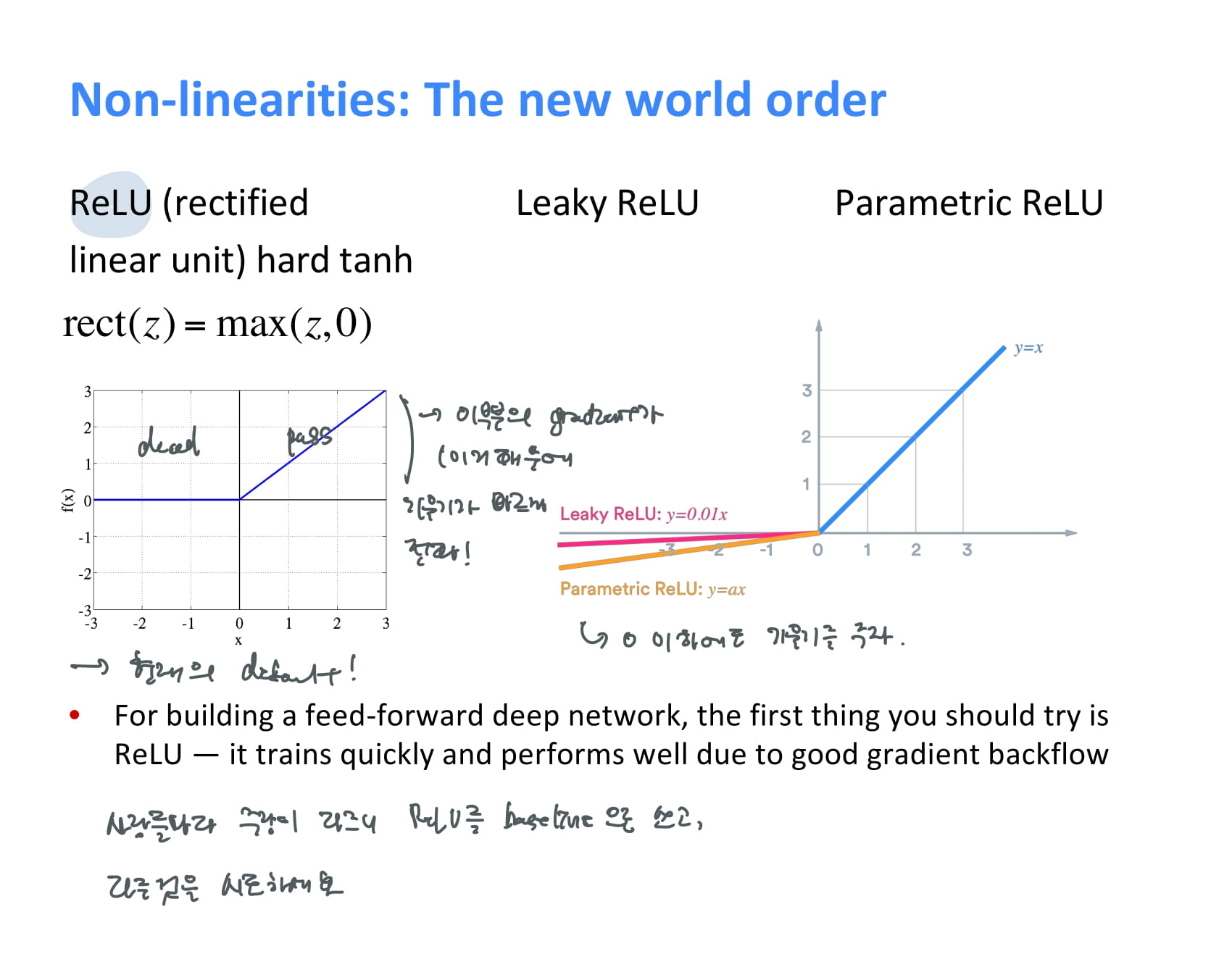
• ReLU

  현대 딥러닝에서 default로 쓰이는 non-linearity function. hard tanh보다 더 간단하게 x가 0보다 크면 그대로 반환하고, 아니면 그냥 0을 반환한다. 기울기가 빠르게 전파된다는 장점이 있다.

• Leaky ReLU, Parametric ReLU

  x가 0보다 작을 때 조그만 기울기를 주는 ReLU의 변형 버전이다.

그래서 뭘 써야 하나? 교수님은 사람들마다 좋다는 게 다르니 일단 ReLU를 베이스라인으로 쓰고, 다른 것을 시도해보는 것을 추천했다.

파라미터를 어떤 값으로 초기화하는지도 학습에 있어 중요한 요소 중 하나이다. 보통은 작은 랜덤값으로 초기화해준다.

Xavier initialization이란 기법도 많이 쓰이는데, 파라미터의 input 개수와 output 개수를 이용해 초기화 값의 범위를 정해주는 방식이다.

파라미터의 범위가 커지면 기울기 전파가 어려워질 수 있으므로, 파라미터가 많을수록 더 표준편차가 작아지도록 초기화를 해준다.

다음으로는 Optimizer에 대한 얘기다.

지금까지 배운 SGD도 괜찮지만 learning rate를 직접 정해줘야 한다는 단점이 있다.

이러한 방식이 믿음직스럽지 못하다면, 현재까지 계산한 기울기 값에 따라 learning rate를 알아서 조절해주는 adaptive optimizer를 사용할 수도 있다.

이런 optimizer들은 보통 지금까지 파라미터 업데이트를 얼마나 했는지에 따라, 많이 하지 않았다면 큰 learning rate로 학습하고, 많이 했다면 학습이 마무리되고 있다고 가정해 작은 learning rate로 학습한다.

learning rate를 직접 정해줄 것이라면, 보통 10의 배수를 사용한다.

learning rate가 너무 큰 경우 훈련의 마지막 단계에서 모델이 converge하지 않을 수 있고, 너무 작은 경우 학습이 느릴 것이다.

따라서 훈련이 진행될수록 작아지도록 하는 것이 좋은데, 일정 epoch마다 반씩 줄여주거나, 공식을 이용해서 조금씩 줄여줄수도 있다.

앞서 설명한 adaptive optimizer들도 learning rate를 사용하긴 하지만 그 값을 계속해서 사용하는 게 아니라, 초기값으로만 사용한다.