[CS224N] Lecture 3 – Word Window Classification, Neural Networks, and Matrix Calculus
Stanford CS224N
목록 보기
2/4



- 분류의 기본 셋업
- 보통 샘플로 구성된 훈련셋이 있음
- 샘플은 (inputs) 과 (labels)로 구성

- 전통적 분류에서는 input이 고정되어있다 가정하고, 각 input에 곱해지는 weight를 이동시키며 input들을 가장 잘 나눠주는 경계선 학습
- 이러한 방법론을 따르는 softmax classifier나 logistic classifier나 linear classifier임, 즉 클래스들을 구분하는 경계선이 line이다.

- softmax classifier를 자세히 들여다보자. x가 y 클래스에 속할 확률은 다음과 같이 계산한다.
- : 클래스별 weight를 저장하는 의 y번째 row(y 클래스에 대한 weight)를 가져와서 x와 곱한다. 이것을 모든 클래스에 대해 수행한다. → 라 하자.
- 각 클래스 y에 대해 계산한 결과를 normalize해 확률로 만들어주기 위해, 모든 클래스에 대해서 를 계산한 값을 모두 더한 후 각 클래스의 를 나눠준다.

- 훈련의 목적은 훈련셋 x, y에 대해 x가 y로 분류될 확률을 최대화하는 것
- 이것은 x가 y가 아닌 다른 클래스로 분류될 확률을 낮추는 것과 같은 말이다.
- negative log: x = 0~1일때 ~0

- 두 확률분포 사이의 차이를 계산하는 법 - cross entropy
- 실제 클래스별 확률과 모델이 예측한 클래스별 확률의 로그값을 클래스마다 더한 후 negate한다.
- 실제 확률분포 p에서는 맞는 클래스의 확률값만 1이고 나머지는 모두 0이다.
- 따라서 의 값은 정답인 클래스의 negative log probability이다.

- full dataset에 대한 cross entropy를 구하기 위해서는 모든 데이터셋에 대해 cross entropy를 계산한 후 평균을 낸다.

- 는 일반적으로 class에 대한 weights로 구성된다.
- 따라서 우리는 decision boundary를 업데이트하기 위해서 와 같은 shape의 기울기값을 계산해야 한다.

- 기존에 사용하던 단순한 분류기들은 모두 경계선이나 경계면을 그리는 단순한 방법이었다. 따라서 복잡한 문제는 해결할 수 없다는 한계가 있었다.

- 신경망을 이용하기 시작하면서, 더 복잡한 문제도 해결할 수 있게 되었다.

- 딥러닝으로 자연어처리를 할 때에는 보통 weight(parameter)와 word vector(representation)을 모두 업데이트한다.
- 즉 클래스에 대한 weight뿐만 아니라 word representation까지도 파라미터로 다루어져야 하기 때문에 파라미터는 Cd+Vd 차원이 된다. (C: 클래스 수, V: vocab 단어 수, d: 벡터 차원)
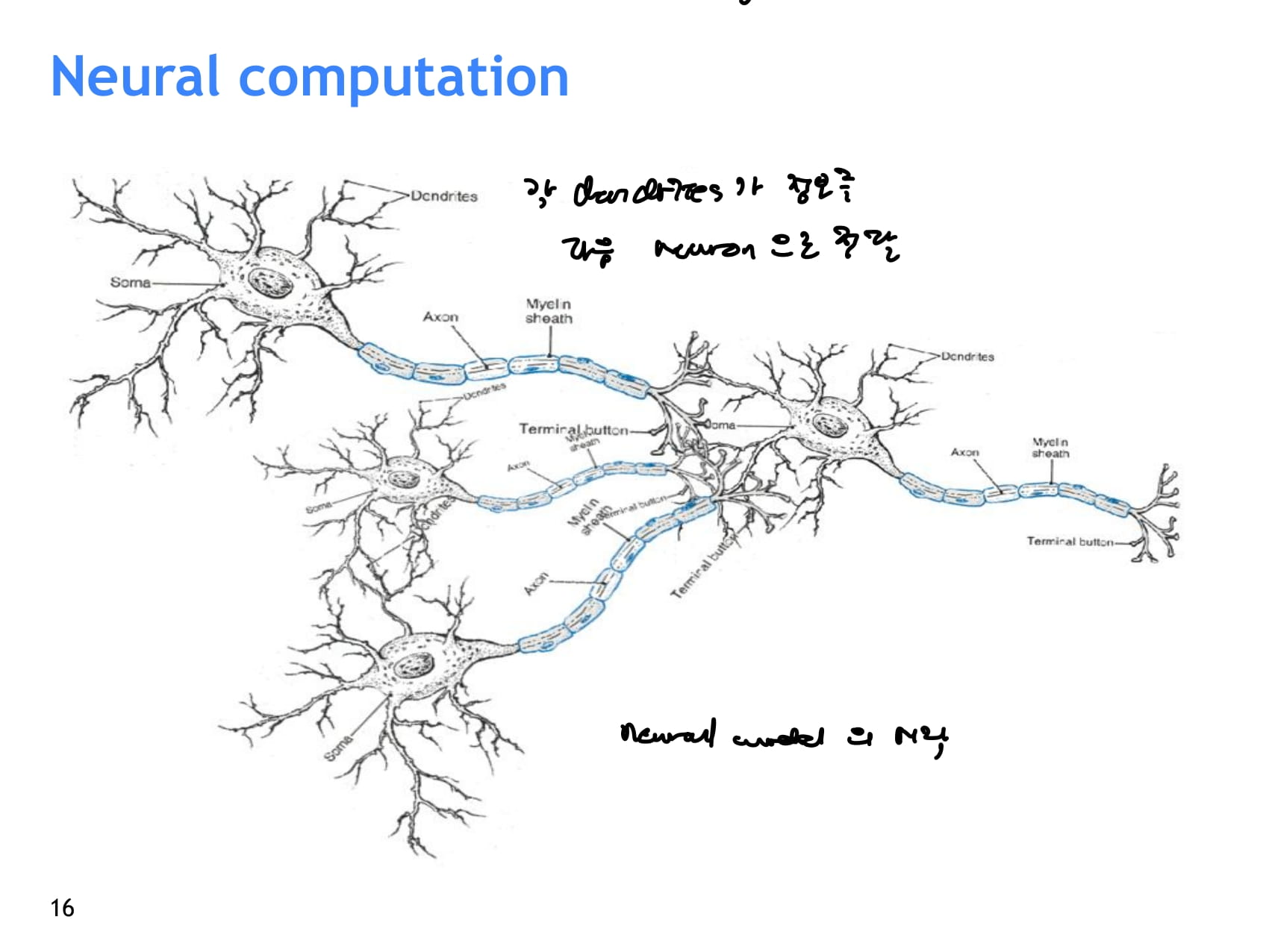
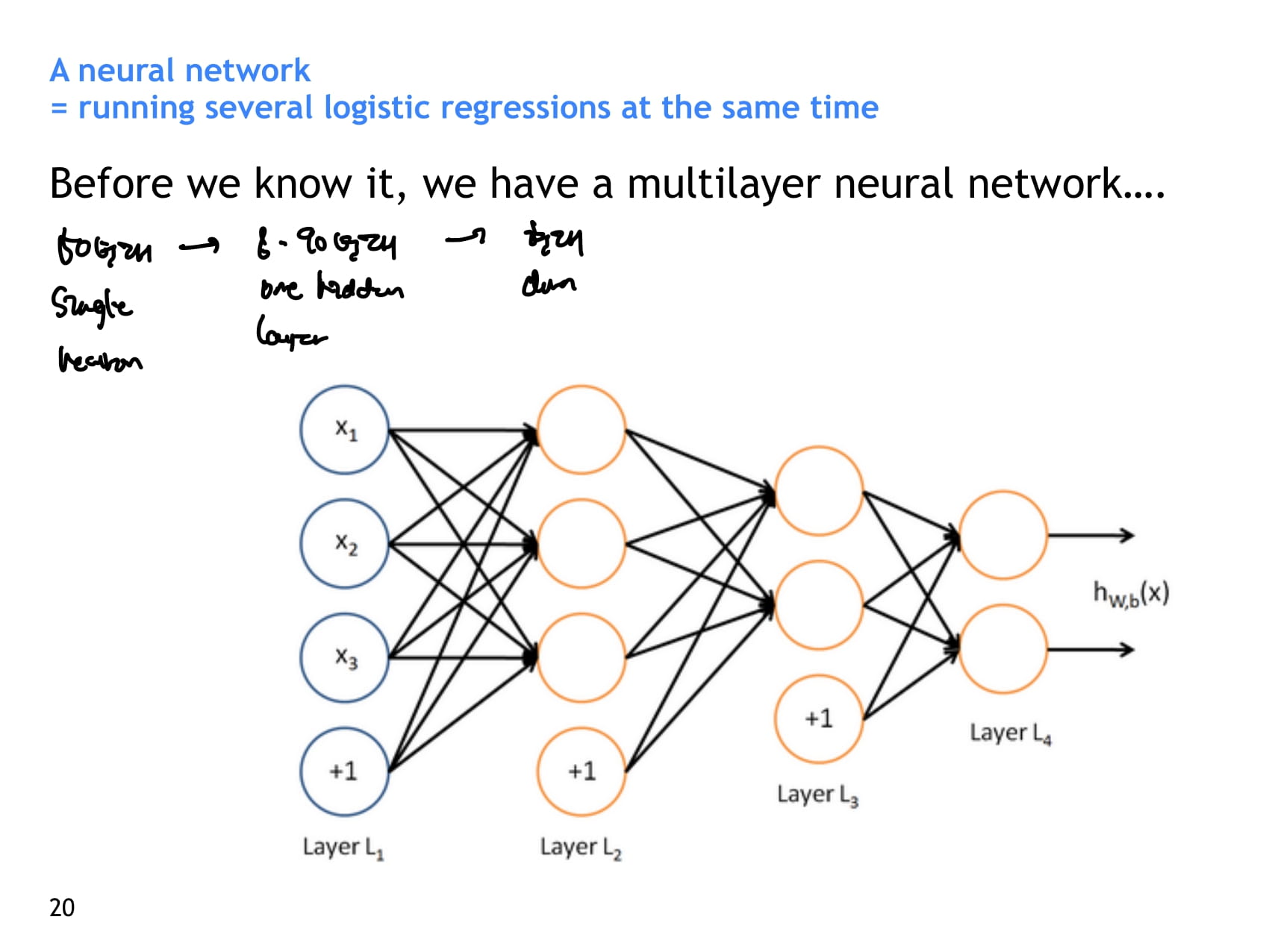
- 맨날 보는 신경망
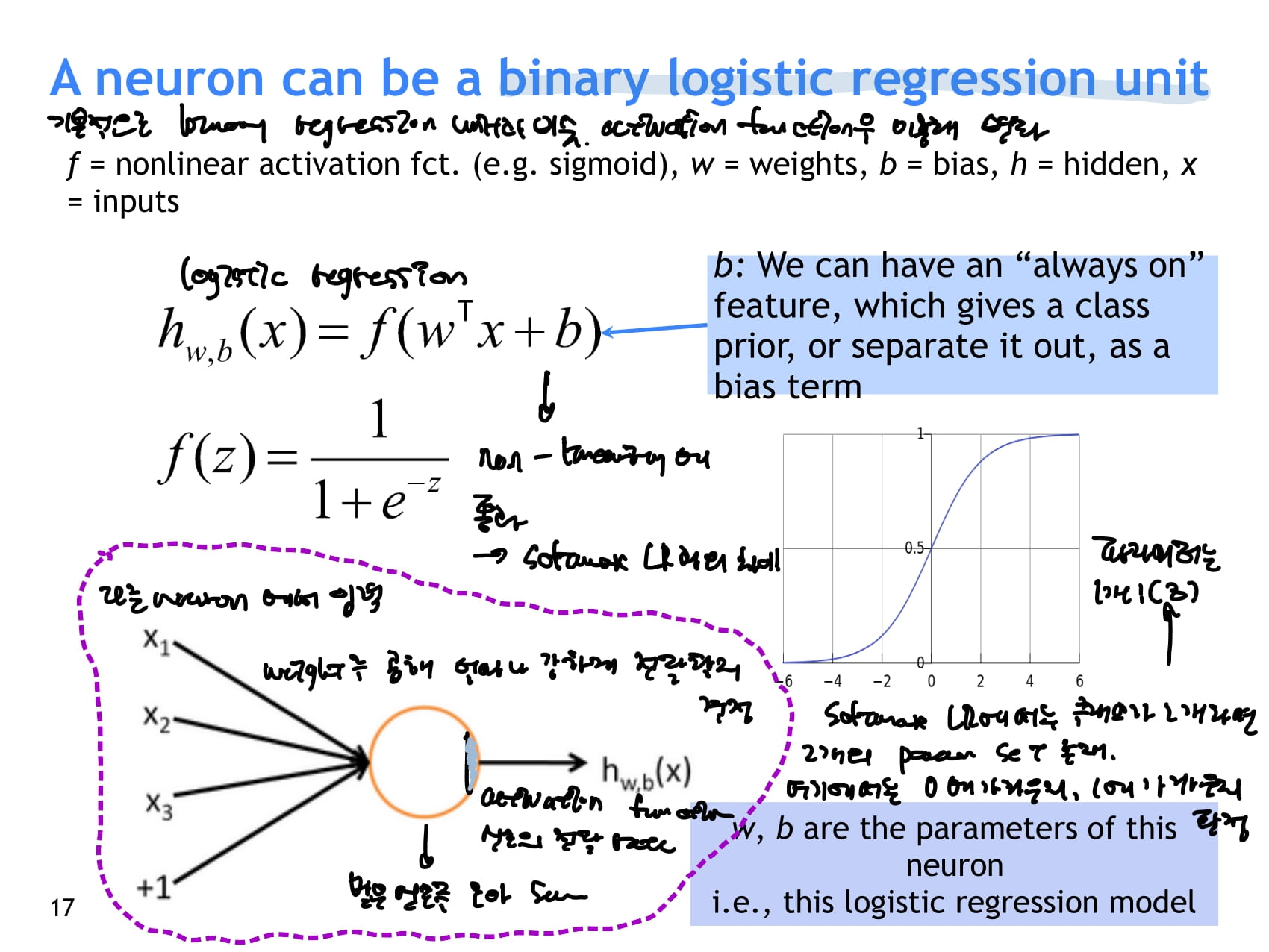
- neuron 하나하나가 하는 일은 기본적으로 input을 받아서 weight를 곱하고 bias를 더해주는 binary regression unit과 비슷하다. 하지만 여기에 activation function을 이용해 비선형성을 더해준다.
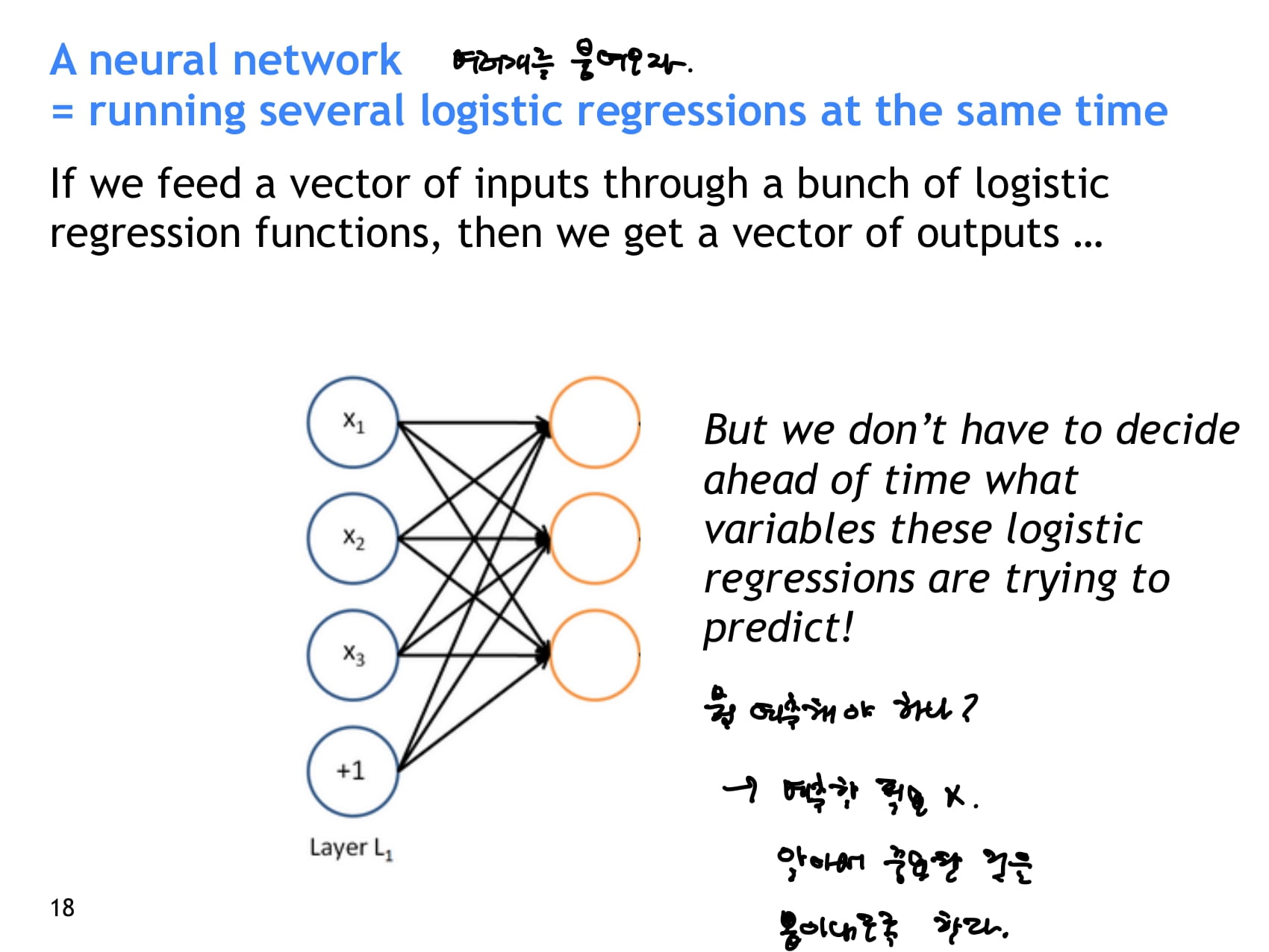
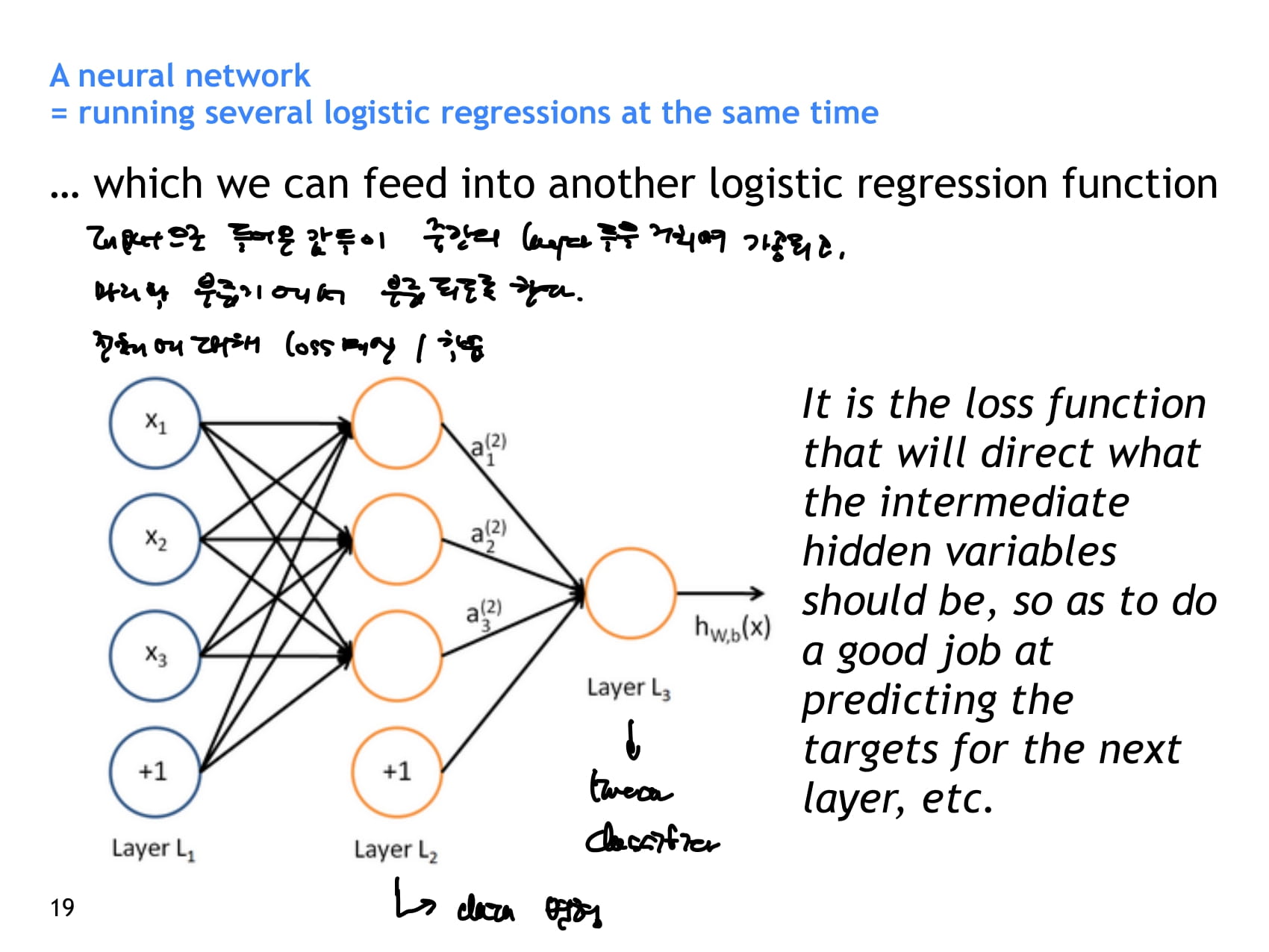
- 여러 layer를 거치며 계산된 값을 다시 linear classifier에 통과시켜 분류 과제도 해결할 수 있다.
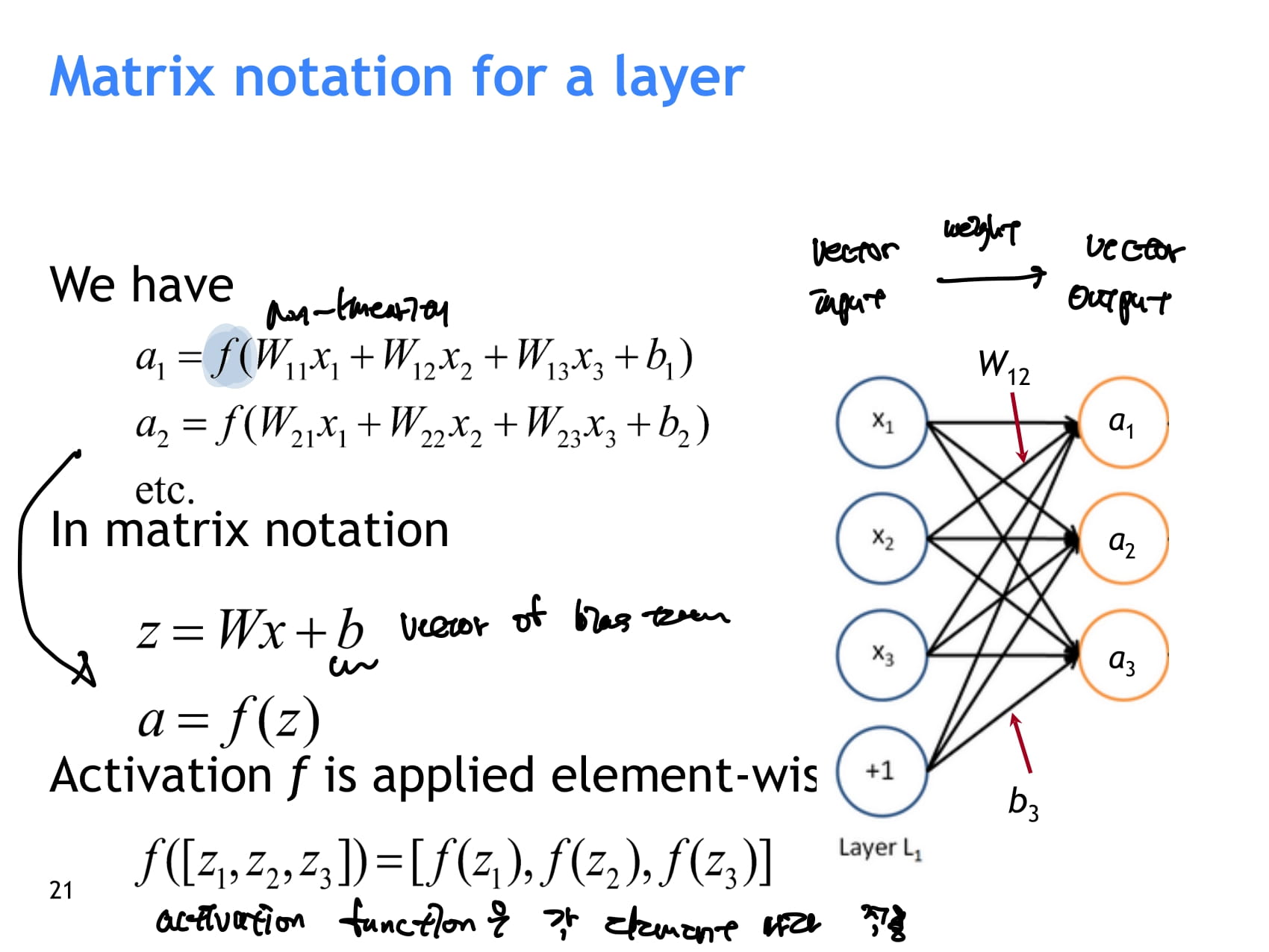
- activation function은 각 element마다 계산된다.
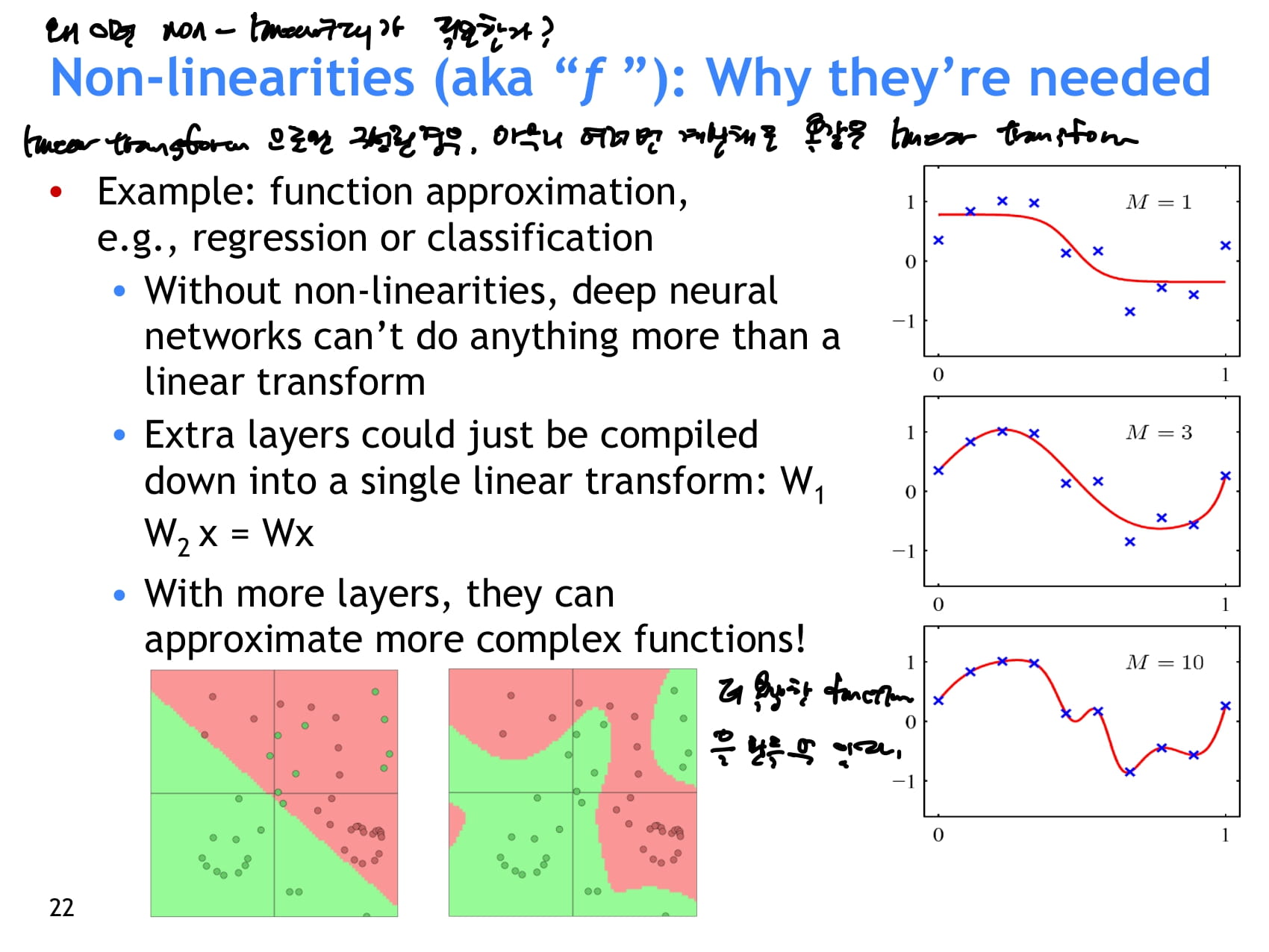
- 왜 non-linearity(비선형성)이 필요한가?
- linear transform으로만 구성된 경우, 아무리 여러 레이어를 쌓아도 똑같은 linear transform이다.
- 비선형성을 통해 더 복잡한 function을 만들 수 있다.

- 자연어 처리 과제 중 NER 소개
- 각종 고유명사를 추출해 분류하고, 관계를 파악하는 과제


- 왜 NER이 어려울까?
- entity의 경계를 구분하기 힘들다
- entity인지 아닌지 판단하기도 어렵다
- 본 적 없는 entity는 어떡하지?

- context 기반으로 단어를 분류해보자.
- 단순하게 window 안의 단어 벡터를 모두 평균내 분류에 사용할 수 있다.
- 하지만 이렇게 하면 각 단어의 위치 정보를 사용하지 못한다.

- 그러면 window 내 word를 모두 concat해서 더 큰 벡터를 만들어보자.
- concat 결과 벡터는 단어 수 * embedding demension 차원

- 벡터를 이어붙여서 더 어려워보일 수 있지만 앞서 배운 softmax classifier로 똑같이 분류할 수 있다.
- word vector 업데이트도 목적함수 미분해서 수행하면 됨

- NER 연구 예시 소개 - window 가운데 단어가 location named entity인지 아닌지에 대한 점수를 계산한다.
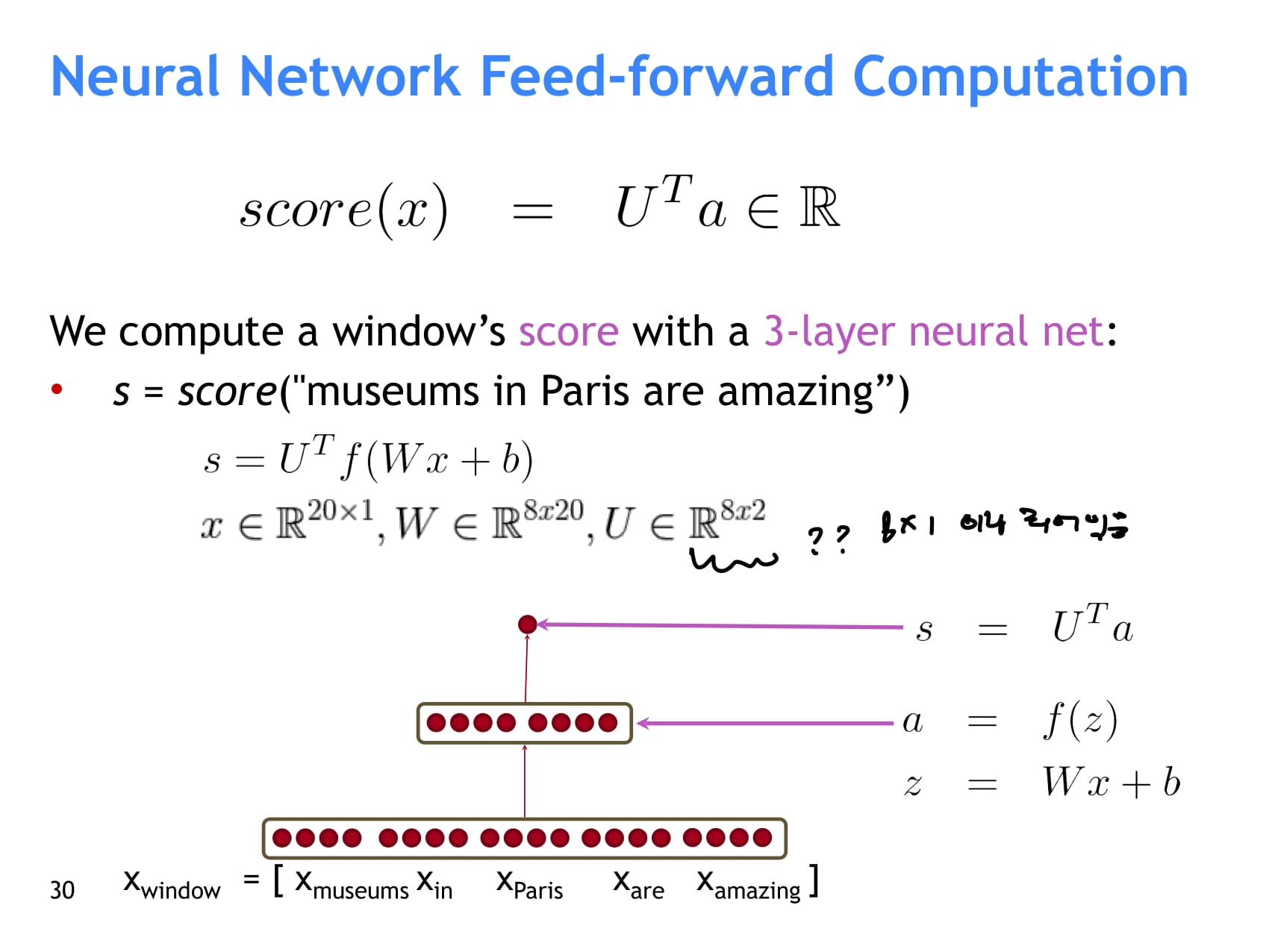
- 먼저 window 내 단어 벡터를 모두 concat한다.
- concat한 벡터에 Weight를 곱하고 bias를 더한 후, activation function을 통과시킨다. → a
- 여기에서 8은 hidden layer의 neuron이 8개인 경우를 가정
- 마지막으로 8x1 shape인 U를 a에 곱해 최종 점수를 계산한다.
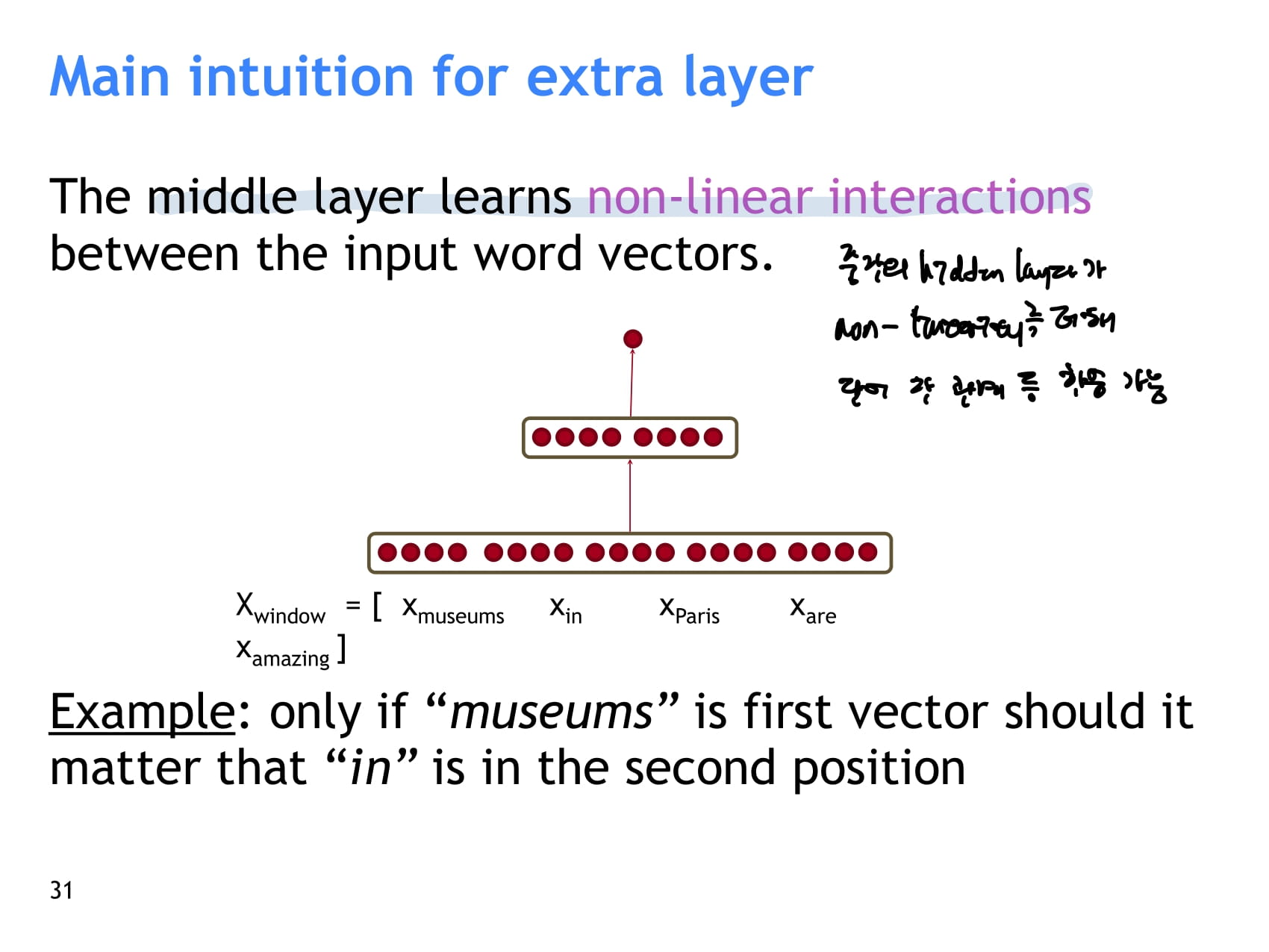
- 중간의 hidden layer가 비선형성을 더해 단어 간 관계 등 기존 선형 분류에서는 학습하지 못하는 복잡한 관계를 학습할 수 있다.


- 교수님이 스킵함

- neuralnet에서도 파라미터를 업데이트하는 방법은 SGD와 다르지 않다
- 여기에서부터는 ToBigs의 스터디자료가 잘 정리되어 있어 참고했다.


- input이 여러개, output이 여러개인 함수를 미분하는 경우 편미분값의 행렬을 계산하는것과같다 (Jacobian matrix)

- 그럼 이 경우 chain rule은 어떻게 적용할까? 변수가 하나일 때 미분값을 곱해주는것과 같이, jacobian matrix를 곱해주면 된다.


- activation function을 입력값 에 대해 미분하는 예시를 보자. activation function 또한 input이 여러개, output이 여러개이므로 미분 결과는 jacobian matrix의 형태가 된다.
- 이 때 는 에만 영향을 준다. 한 뉴런에 대한 input이 다른 뉴런에도 영향을 주지 않기 때문이다.
- 그러므로 위 식에서 는 일때만 이며 다른 경우에는 0이다.
- 가 에 대해 가 주는 영향을 의미한다는 것을 기억하자.
- 따라서 는 의 대각행렬이 된다.

- 이기 때문에 이다.
- 두 벡터를 내적하고, 한 벡터에 대해 미분하면 다른 벡터의 전치가 되기 때문에
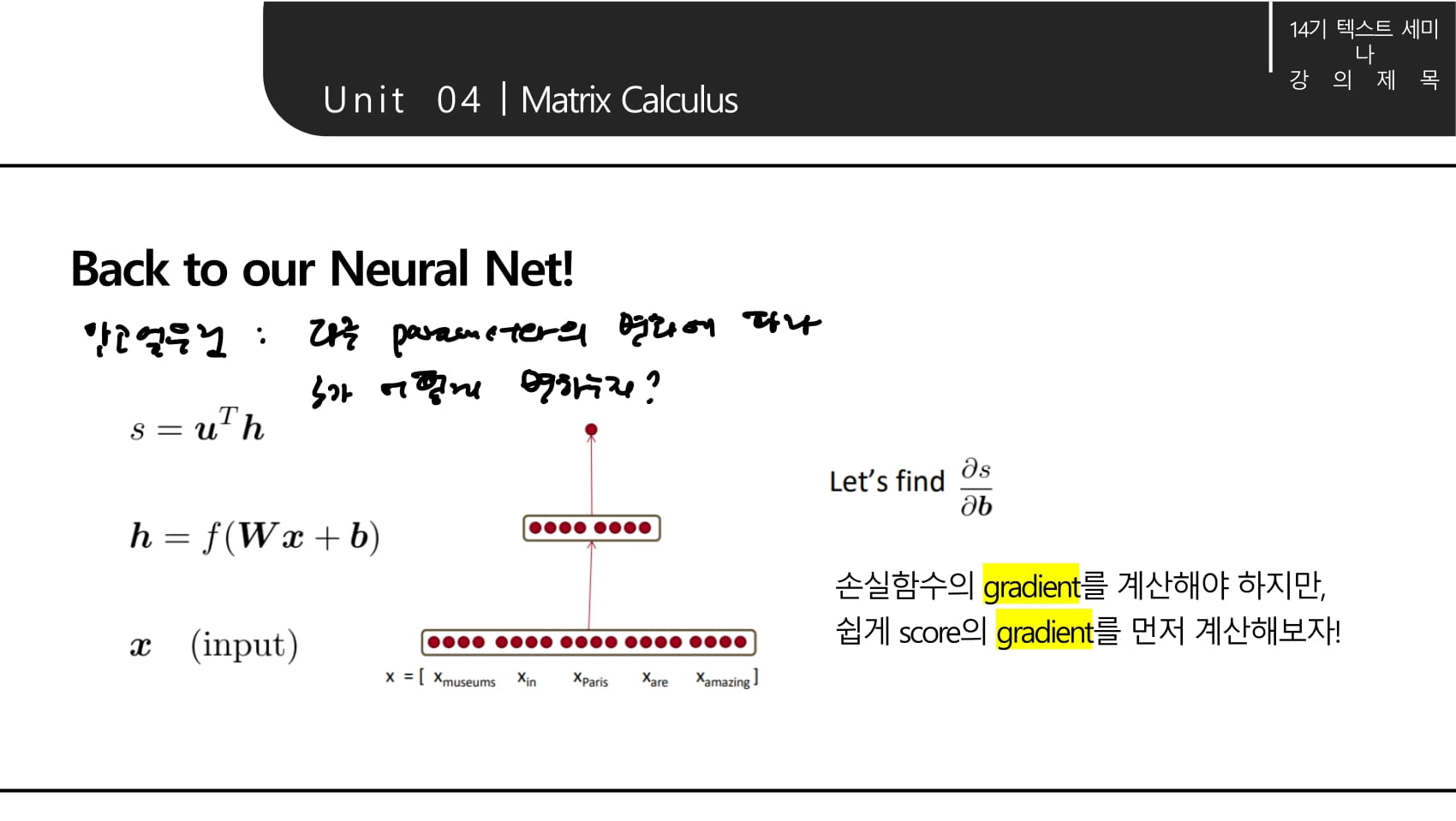
- 여기에서 알고싶은 것은 각 파라미터의 변화에 따라 최종 결과 s가 어떻게 변하는지이다.

- 수식들을 최대한 쪼개야 chain rule을 적용하기 용이하다.


- 앞서 계산한 값들의 총집합!


- 여기에서 local error signal을 라는 변수에 저장해 재사용할 수 있다. 는 다음 강의에 나올 upstream gradient를 의미하는 것 같다.

- 앞서 소개한 원칙대로라면 output이 하나이고 input이 nm shape인 경우, 미분값은 1 nm shape의 jacobian matrix여야 하지만 편의상 업데이트할 파라미터의 shape를 따라가도록 한다.
- 앞으로도 관례적으로 이렇게 계산할 것이다.

- 수학적으로는 이해가 안되는 Transpose를 해주는 것도 weight shape와 맞춰주기 위함
