K-最近傍法(K-Nearest Neighbor)は、機械学習で使う分類(Classification)アルゴリズムだ。類似した特徴を持つデータは、類似したカテゴリに属する傾向があるという前提で使う。
K-最近傍法アルゴリズムの概念
原理を理解しやすくするために、図を参考にする。
下の図を見る。すべてのデータ(点)にはそれぞれ x 値と y 値がある。そして点の色で緑と赤に分けて分類を示す。また、白い点はまだ分類されていない新しいデータだ。K-最近傍法アルゴリズムの目的は、このように新しい点が出現したときにそれを緑や赤に分類することだ。
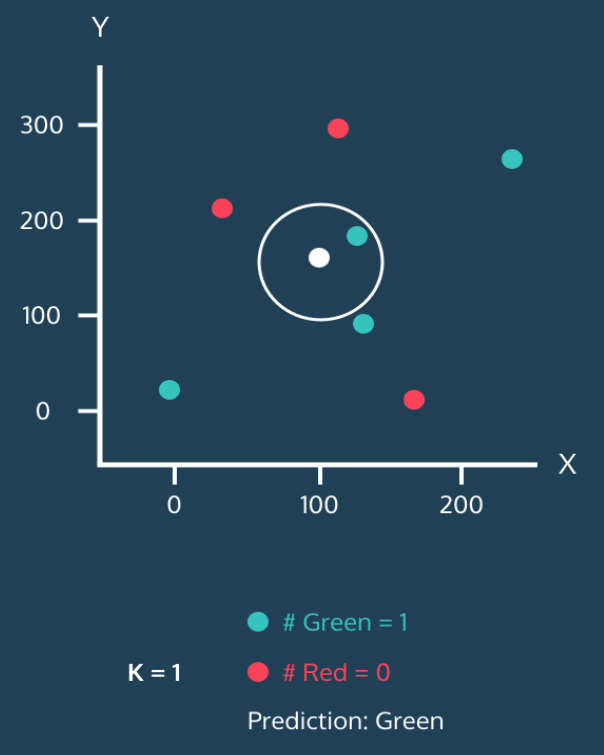
白い点の周囲に円を描き、この円の中には 1 つの近傍がある。このように円の中に含まれる近傍の数を k と考える。上の図では k=1 で、白い点は緑に分類される。
次に円を拡大してみる。k を 2 に調整して、最も近い近傍の数を 2 つに増やす。
近傍 2 つはどちらも緑だ。この場合も白い点は緑に分類される。
次に最も近い近傍の数を 3 つに増やす。
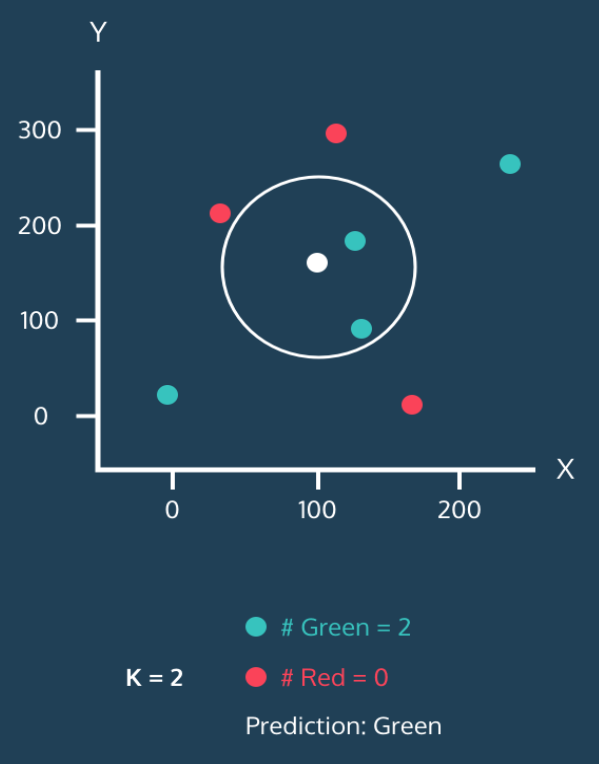
緑が 2 つ、赤が 1 つだ。依然として緑が多いので、白い点は緑に分類される。一種の多数決だ。
最も近い近傍の数を 4 つに増やす。
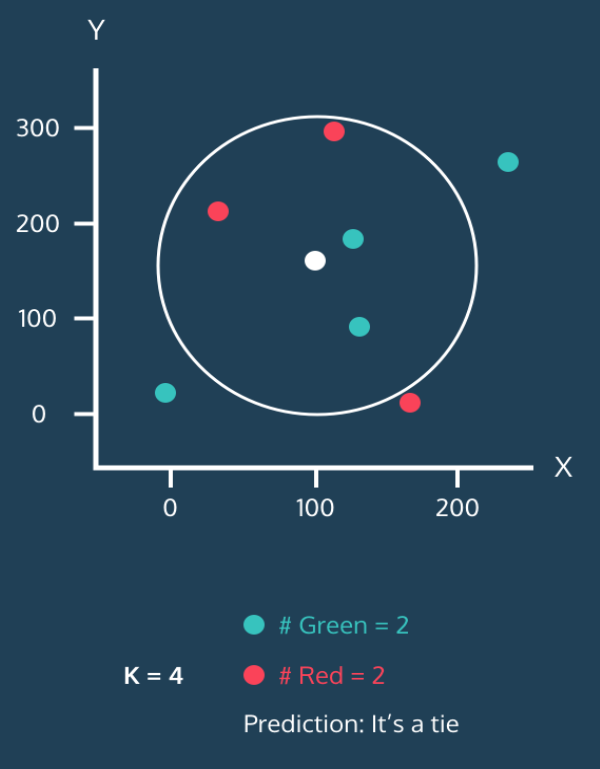
緑が 2 つ、赤が 2 つだ。引き分けになった。
この場合は少し困る。最初から k を奇数に設定すれば、このような問題は起こらない。もちろん、引き分け(tie)になった場合の処理方法はいくつかある。例えば、最も近い近傍に従うとか、ランダムに選ぶとかだ。しかし、データが十分にあれば、いずれにせよ結果はほぼ同じになるので、それほど心配する必要はない。
最後に k を 5 に増やすと、円が拡大し、近傍の中で赤が 3 つ、緑が 2 つになるので、白い点は赤に分類される。
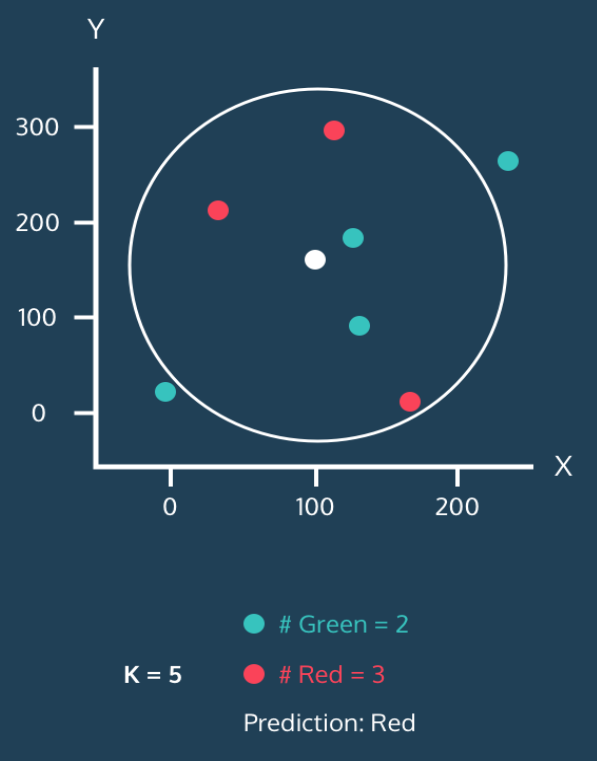
これが K-最近傍法アルゴリズムの核心概念だ。既に各点の分類が分かっていれば、新しい点が出現したときにそれをどこに分類するか決めることができる。
しかし、このアルゴリズムにはいくつか考慮すべき問題がある。
1. 正規化(Normalization)
上の例では x 値と y 値が適度に広がっているので問題はないが、実際のデータではそうではない。例えば、成人男女の年収と視力を特徴(feature)として考えてみよう。年収の単位が円だと偏差が数千万単位を超えるが、視力は小数点まで計算しても最大値と最小値の偏差が 10 未満だ。それを同じ基準で考慮して反映すると、年収が圧倒的に反映されるため、不合理な結論が出る可能性がある。
だから、K-最近傍法アルゴリズムを使うときは、すべての特徴を均等に反映するために正規化(Normalization)を行うことが多い。正規化の方法にはいくつかあり、最も広く使われる方法は以下の二つだ。
- 最小値を 0、最大値を 1 に固定して、すべての値を 0 と 1 の間の値に変換する方法
- 平均と標準偏差を使って、平均からどれだけ離れているかを z スコアに変換する方法
これ以外にも他の方法があり、それぞれに利点と欠点があるが、通常は上記の方法を適切に使って特徴を正規化するとある程度は解決する。ただし、正規化が常に最善策とは限らない。機会があれば、別の投稿で詳しく説明する。
2. K の数の選択
もう一つ重要な問題は「k をいくつに設定するか」だ。これはすべての値を実際にテストして分類精度(Accuracy)を計算する過程で手がかりを見つけることができる。
k が小さすぎる場合:過適合(Overfitting)
まず、k が小さすぎる場合を考える。極端に言えば、k=1 としよう。この場合、分類精度はかなり低くなる。視野が狭くなり、非常に近くにある点 1 つに敏感に影響されるためだ。これを過適合(overfitting)と言う。過適合は機械学習アルゴリズムで非常に重要な概念なので、必ず理解しておこう。とにかく、K-最近傍法アルゴリズムでは周囲の他の近傍を十分に考慮しないと過適合が発生する。そのため、1 つの異常値(outlier)がある場合、その近くにある点のラベルがその異常値によって決まることがある。
下の図を見る。

図の左上の黒い点は異常値のようだ。もし k=1 でその近くにデータが位置すると、緑に分類されず、異常値に従って濃い青に分類されてしまう。
k が大きすぎる場合:過少適合(Underfitting)
一方、k が大きすぎる場合は過少適合(underfitting)が発生する。過少適合は、分類器が学習セットの細かい部分に十分な注意を払っていないために起こる。例えば、学習セットに 100 個の点があり、k=100 に設定したと極端に仮定しよう。この場合、すべての点が最終的に同じ方法で分類される。点の間の距離は意味を失う。もちろん、これは極端な例だが、いずれにせよ k が大きすぎると分類器が学習データを十分に細かく見ることができないということだ。
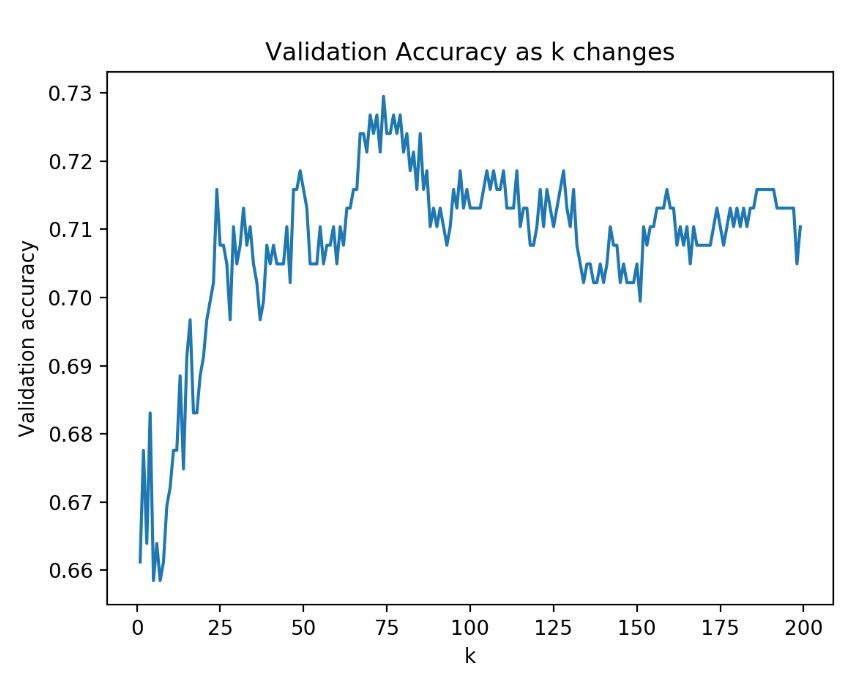
分類モデルを作成するとき、一部のデータは検証用に取り分け、学習データだけでモデルを作成し、検証データを使って精度(Accuracy)を確認することができる。以下のグラフは、ある分類モデルで k 値を変化させながら分類精度を確認した例だ。
k が小さすぎると過適合が発生して精度が相対的に低い。反対に k が大きすぎても過少適合が発生して精度が低下し始める。最終的には 75 付近で最も高い精度を示す。
この程度まで考慮できれば、K-最近傍法アルゴリズムを概念的に理解したと言える。具体的に点の間の距離を計算する方法も重要だが、それはこの投稿を参考にしてほしい。
核心要約
K-最近傍法アルゴリズムの核心内容を要約すると、以下のように整理できる。
- n 個の特徴(feature)を持つデータは n 次元の空間に点として概念化できる。
- 類似した特徴を持つデータ同士は距離が近い。距離公式を使ってデータ間の距離を求めることができる。
- 分類が分からないデータに対して最も近い近傍 k 個の分類を確認し、多数決を行うことができる。
- 分類器の効果を高めるためにパラメータを調整することができる。(K-最近傍法の場合、k 値を変更できる)
- 分類器が不適切に学習すると過適合や過少適合が発生する。(K-最近傍法の場合、k が小さすぎると過適合、大きすぎると過少適合が起こる)
