우선순위 큐
우선순위 큐의 이해
우선순위 큐 라고해서 앞서 배운 큐를 떠올리는건 당연하지만
우선순위 큐와 큐는 큰 차이점이 있기에 다른 개념이라고 생각하는 것이 쉽다
가장 큰 차이점으로는 큐는 줄서기로 먼저 줄을 선사람이 먼저 입장하는 거라면
우선순위 큐는 응급실을 떠올리면 된다
감기환자 보다 교통사고 환자가 더 먼저 치료를 받는것처럼
우선순위에 따라 데이터를 접근한다
우선순위 큐의 구현 방법
- 1.배열을 기반으로 구현
- 2.연결 리스트 기반 구현
- 3.힙 기반 구현
1.배열을 기반으로 구현
배열을 기반으로 우선순위 큐를 구현 하는 방법은
간단하게 우선순위가 높은 데이터를 배열 앞쪽에 차곡차곡 위치시키면 된다
하지만 배열을 기반으로 구현하는 방식의 큰 단점은
데이터를 삽입하거나 삭제 과정에서 배열에 데이터들을 한칸씩 전부 이동시켜 줘야한다는 것이다
또한 데이터 추가시에 모든 데이터와 우선순위를 비교해야 하는 문제가 발생할 가능성이 있다
2.연결 리스트 기반 구현
연결리스트도 배열과 마찬가지로 우선순위가 높은 데이터를
앞쪽에 연결하는 방식으로 구현할수 있다
하지만 배열 기반과 마찬가지로 문제점을 가지는데
배열처럼 데이터를 추가 삭제시 한칸씩 이동해야 하는 문제는 없지만
역시 추가시 모든 데이터와 우선순위를 비교해야 하는 상황이 생길수 있다
3.힙 기반 구현
힙은 이진트리 이면서 동시에 완전 이진 트리이다
모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나 같아야 한다
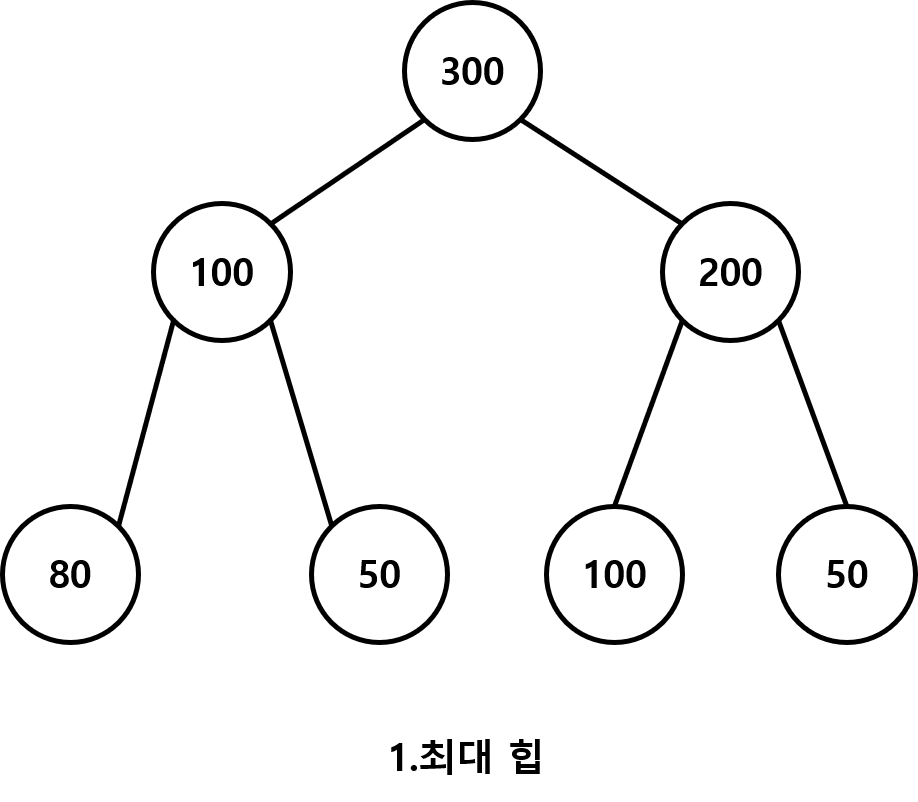
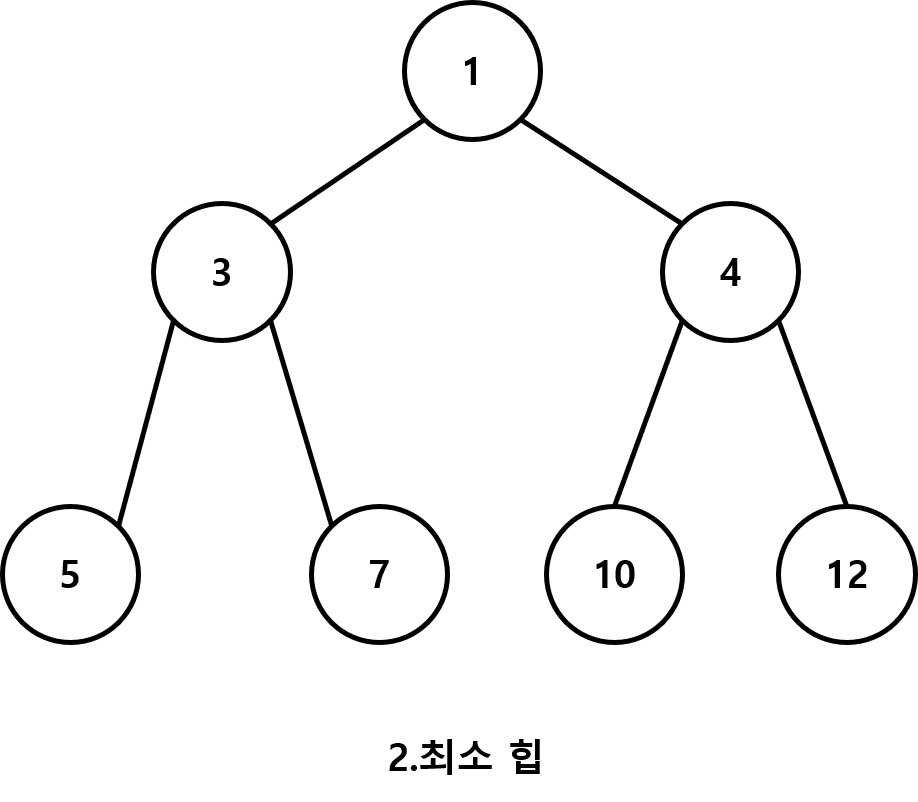
힙은 그림에서 처럼 우선순위에 따라서 데이터를 위치 시킬수 있는 자료구조 입니다.
위로 올라 갈수록 값이 커지게 할수 있고 (최대 힙) 반대로 값이 작아 질수 있다( 최소 힙)
힙에 특징을 활용해서 우선순위 큐를 구현 할수있다
힙 데이터 추가
힙 = 우선순위 큐 라고 생각하는 것은 무리가 있다
물론 저 둘이 환상의 콤비임은 틀림이 없기에 동일시 할수 있지만 결코 같지 않음을 알아놓자
최소 힙을 기준으로 정리해 보자
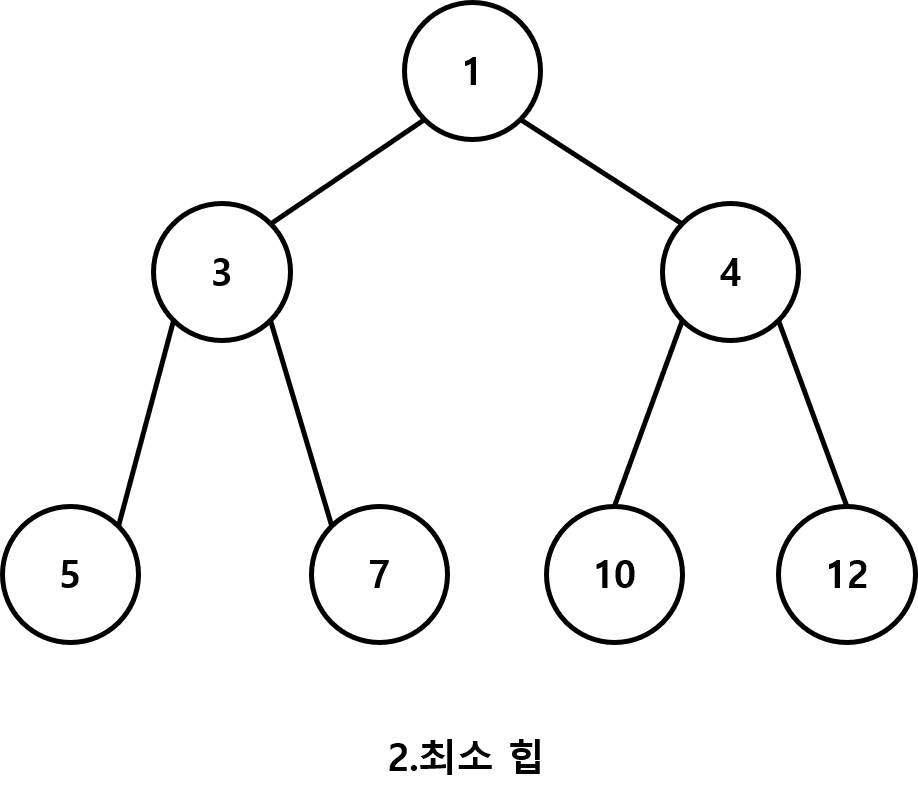
그림처럼 최소 힙이 존재해 있다
여기서 최소 힙의 조건을 정리해 보자
1.자식노드 데이터의 우선순위 <= 부모 노드 데이터 우선순위
2.완전이진트리 이다
위 그림에서 데이터 "2"를 추가하는 과정을 그림으로 이해해 보자
1.새로운 데이터는 우선순위가 제일 낮다고 가정하에서 "마지막 위치"에 저장한다
2.부모 노드와 우선순위를 비교해서 자리를 바꿔준다
(2는 5보다 우선순위가 높음으로 자리가 바꿀것이다)
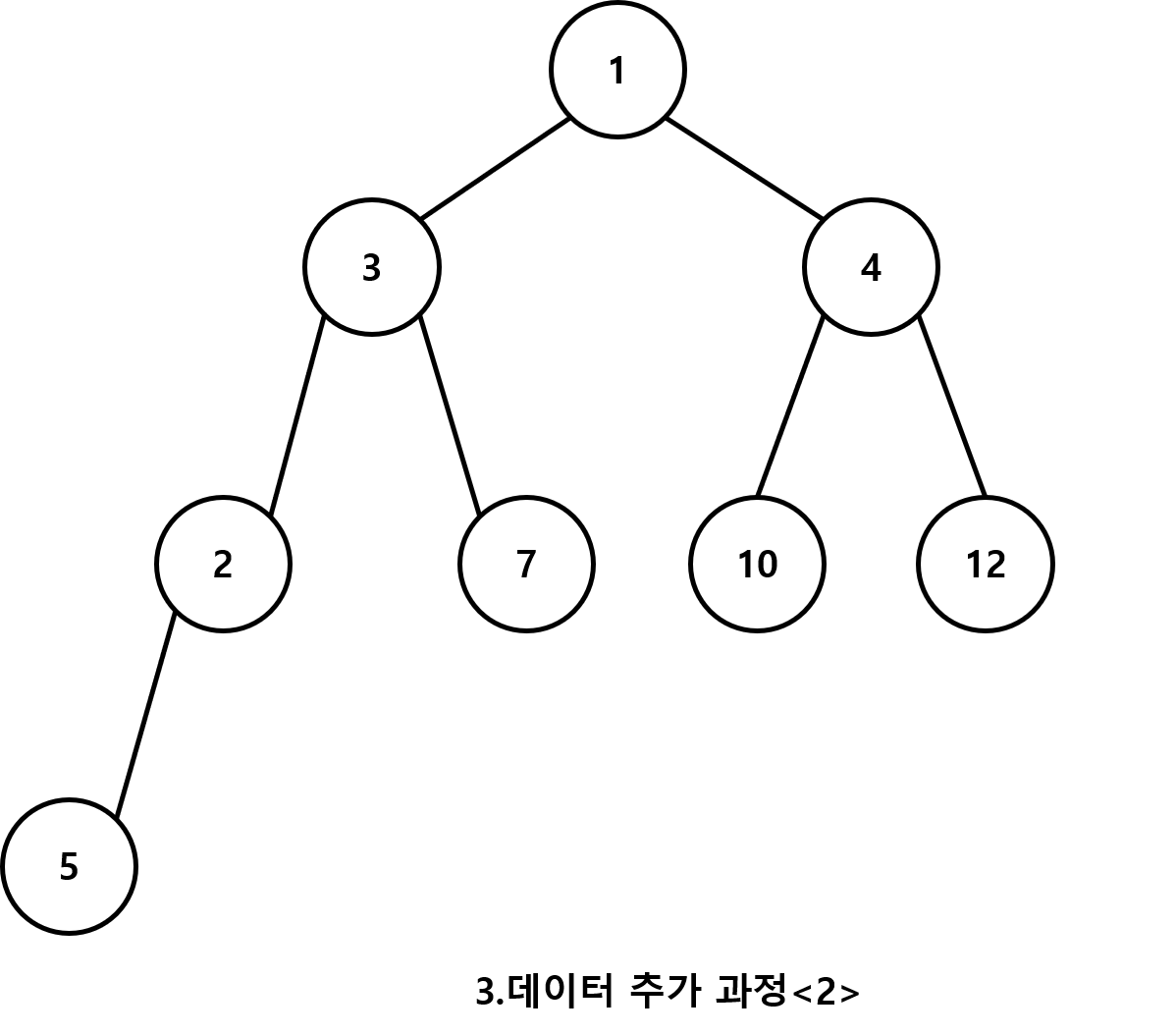
- 2번 과정을 계속 반복해 준다
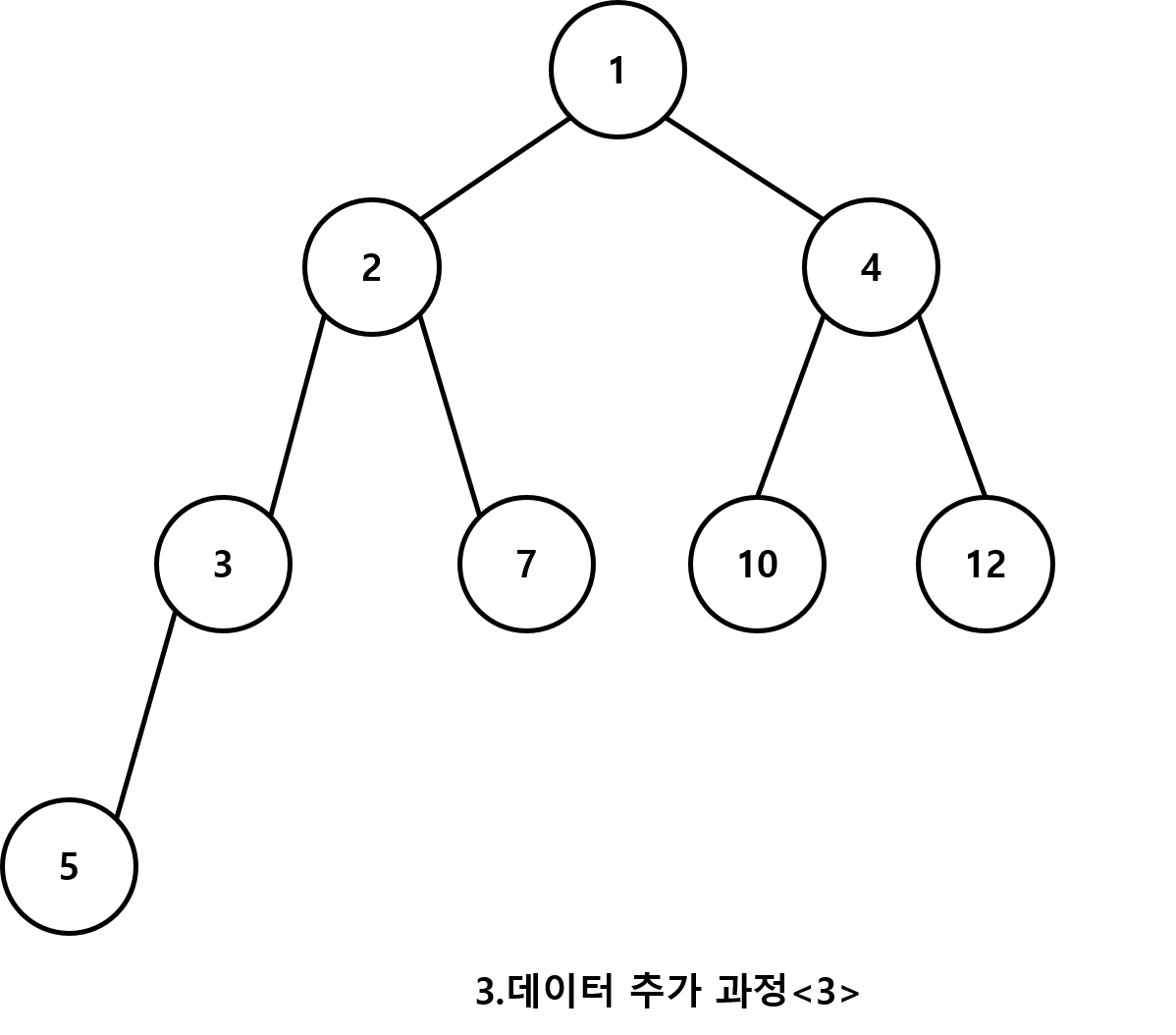이렇게 해서 데이터의 추가 과정을 그림으로 알아봤다
그림으로 설명한 내용을 100%코드로 그대로 옮기지는 않을것을 알아두고 있자힙 데이터 삭제
우선순위 큐에서의 삭제는 "가장 높은 우선순위 데이터 삭제" 를 의마한다
데이터를 삭제하고 난 후로도 완전 이진트리 구조를 유지해야 한다.
1.가장 높은 우선순위 데이터를 삭제한다
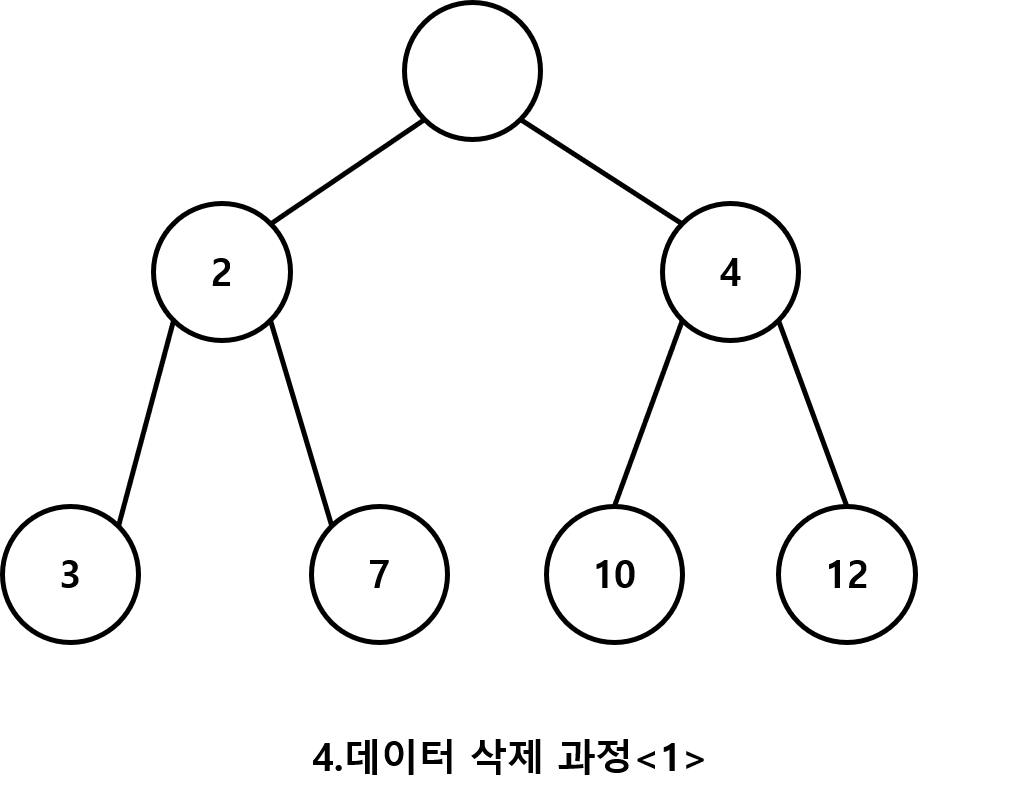
2.마지막 노드를 루트 노드의 자리로 옮긴다
(여기서 마지막이란 마지막 레벨의 가장 오른쪽에 위치한 노드이다)
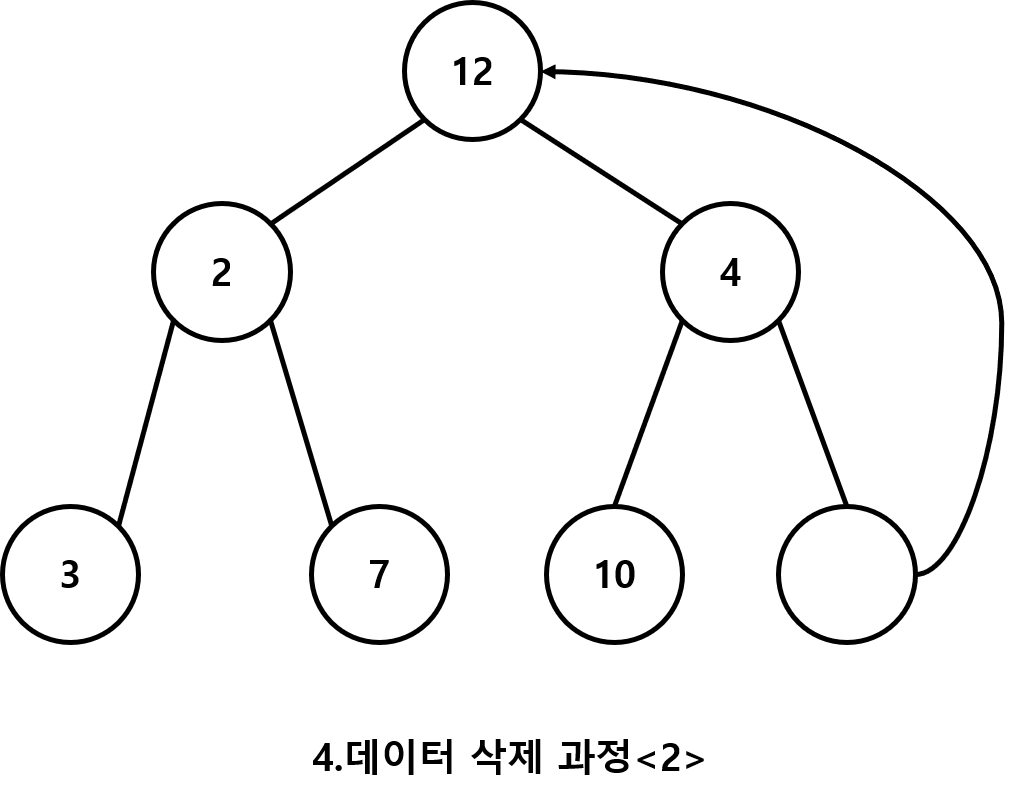
3.두개의 자식노드 중에 우선순위가 높은 자식 노드와 비교후 자리를 바꾼다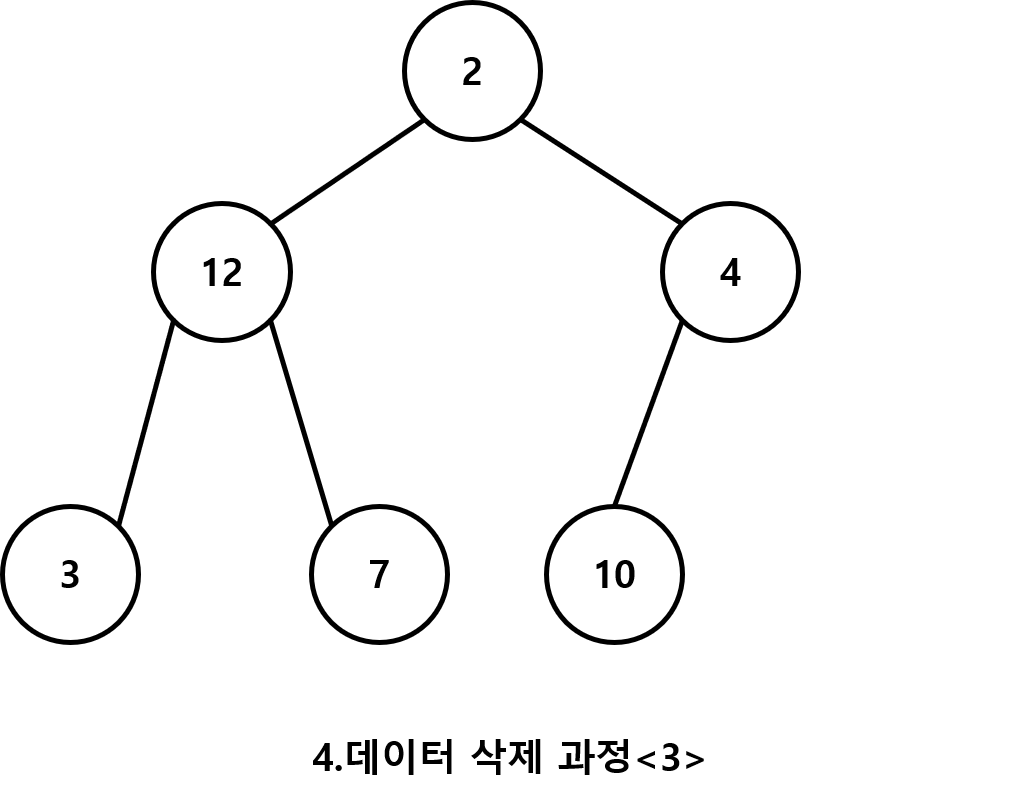
- 3의 과정을 계속 반복한다
힙의 구현
배열을 이용해서 힙을 구현해 보자
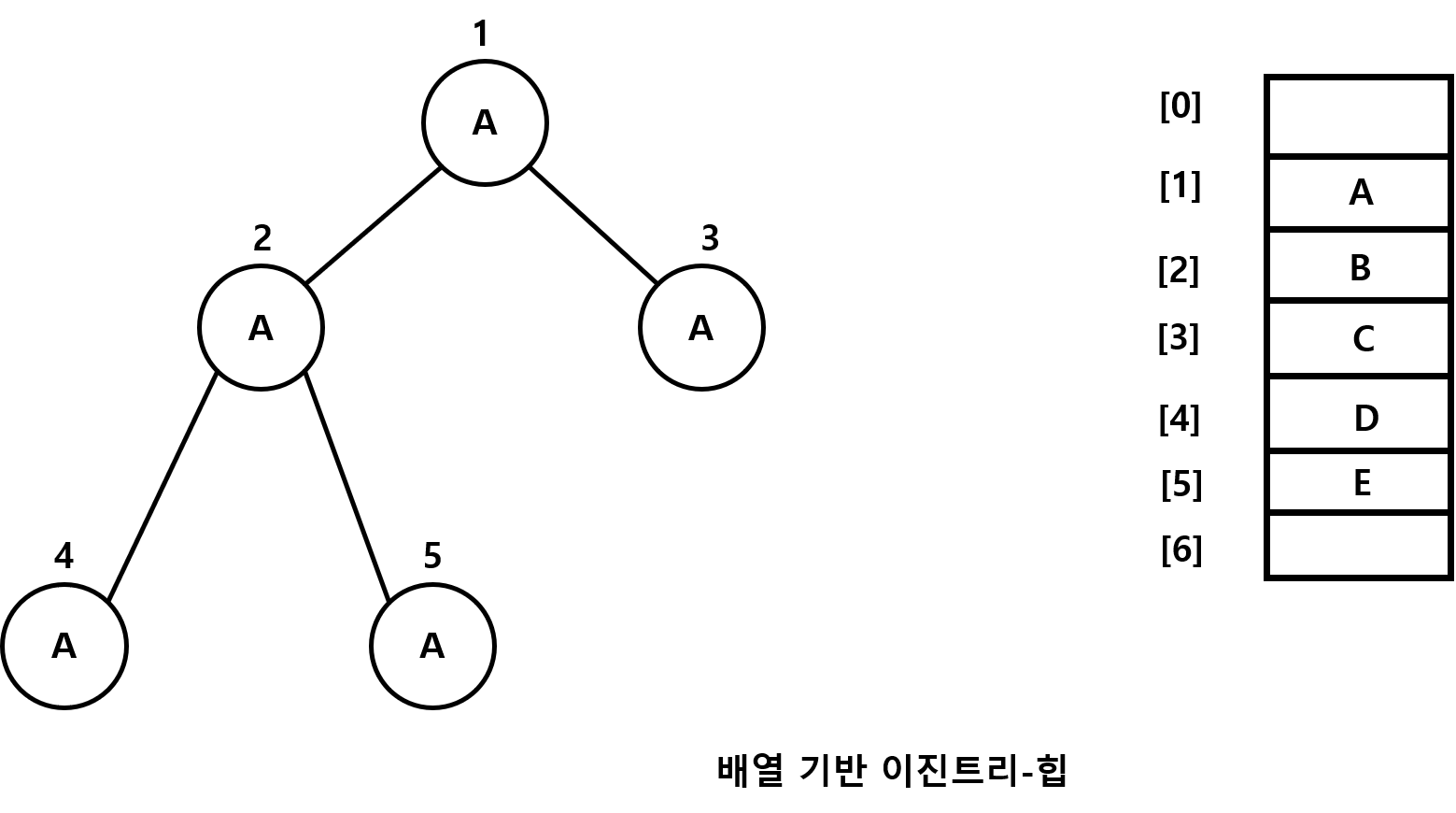
여기서 우리는 몇가지 힙의 규칙을 살펴보자
- 왼쪽 자식 노드의 인덱스 값 = 부모 노드의 인덱스 값 X 2
- 오른쪽 자식 노드의 인덱스 값 = 부모 노드의 인덱스 값 X 2 + 1
- 부모 노드의 인덱스 값 = 부모 노드의 인덱스 값 ÷ 2
힙의 구조체
코드
typedef struct _heapElem
{
int pr; // 값이 작을수록 높은 우선순위 높다
int data;
} HeapElem;
typedef struct _heap
{
int numOfData;
HeapElem heapArr[100];
} Heap;HeapElem은 트리의 노드를 의미하고
Heap은 이제 노드 구조체 배열을 가지는 구조체다
지금부터는 앞에서 그림으로 설명한 데이터 추가 삭제 과정을 코드로 구현한것을 정리해 보자
코드
//1번
void HeapInit(Heap * ph)
{
ph->numOfData = 0;
}
//2번
int HIsEmpty(Heap * ph)
{
if(ph->numOfData == 0)
return TRUE;
else
return FALSE;
}
//3번
int GetParentIDX(int idx)
{
return idx/2;
}
//4번
int GetLChildIDX(int idx)
{
return idx*2;
}
//5번
int GetRChildIDX(int idx)
{
return GetLChildIDX(idx)+1;
}
//6번
int GetHiPriChildIDX(Heap * ph, int idx)
{
if(GetLChildIDX(idx) > ph->numOfData) // 자식 노드가 없다면
return 0;
else if(GetLChildIDX(idx) == ph->numOfData) // 왼쪽 자식 노드가 마지막 노드라면
return GetLChildIDX(idx);
else // 왼쪽 자식 노드와 오른쪽 자식 노드의 우선순위를 비교
{
if(ph->heapArr[GetLChildIDX(idx)].pr
> ph->heapArr[GetRChildIDX(idx)].pr)
return GetRChildIDX(idx);
else
return GetLChildIDX(idx);
}
}
//7번
void HInsert(Heap * ph, HData data, Priority pr)
{
int idx = ph->numOfData+1;
HeapElem nelem = {pr, data};
while(idx != 1)
{
if(pr < (ph->heapArr[GetParentIDX(idx)].pr))
{
ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
idx = GetParentIDX(idx);
}
else
break;
}
ph->heapArr[idx] = nelem;
ph->numOfData += 1;
}
//8번
HData HDelete(Heap * ph)
{
HData retData = (ph->heapArr[1]).data; // 삭제할 데이터 임시 저장
HeapElem lastElem = ph->heapArr[ph->numOfData];
int parentIdx = 1; // 루트 노드의 Index
int childIdx;
while(childIdx = GetHiPriChildIDX(ph, parentIdx))
{
if(lastElem.pr <= ph->heapArr[childIdx].pr)
break;
ph->heapArr[parentIdx] = ph->heapArr[childIdx];
parentIdx = childIdx;
}
ph->heapArr[parentIdx] = lastElem;
ph->numOfData -= 1;
return retData;
}1번 코드
//1번
void HeapInit(Heap * ph)
{
ph->numOfData = 0;
}힙을 초기화 하는 코드이다
2번 코드
int HIsEmpty(Heap * ph)
{
if(ph->numOfData == 0)
return TRUE;
else
return FALSE;
}ph->numOfData은 힙에 저장된 데이터의 갯수(노드 갯수)를 의미한다
3,4,5번 코드
//3번
int GetParentIDX(int idx)
{
return idx/2;
}
//4번
int GetLChildIDX(int idx)
{
return idx*2;
}
//5번
int GetRChildIDX(int idx)
{
return GetLChildIDX(idx)+1;
}int idx은 인자로 넘겨주는 노드의 인덱스 값이다
int idx 1은 루트 노드를 의미한다
int idx에 따라 왼쪽, 오른쪽,부모노드의 인덱스 값을 반환한다
6번 코드
//6번
int GetHiPriChildIDX(Heap * ph, int idx)
{
//6-1번
if(GetLChildIDX(idx) > ph->numOfData) // 자식 노드가 없다면
return 0;
//6-2번
else if(GetLChildIDX(idx) == ph->numOfData) // 왼쪽 자식 노드가 마지막 노드라면
return GetLChildIDX(idx);
//6-3번
else // 왼쪽 자식 노드와 오른쪽 자식 노드의 우선순위를 비교
{
if(ph->heapArr[GetLChildIDX(idx)].pr
> ph->heapArr[GetRChildIDX(idx)].pr)
return GetRChildIDX(idx);
else
return GetLChildIDX(idx);
}
}6-1번
자식 노드가 없는 경우
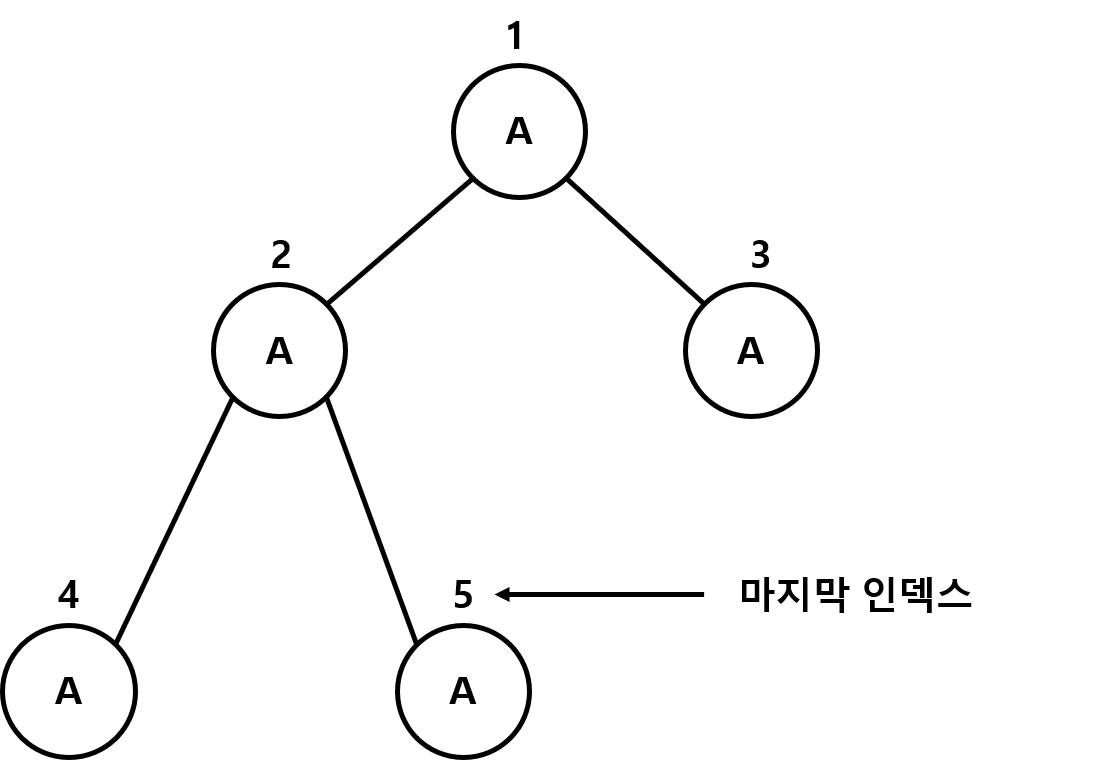
ph->numOfData가 의미하는 바는 완전이진트리의 마지막 노드의 인덱스 값을 의미한다
5번 인덱스 노드의 왼쪽에는 자식 노드가 존재하지않는다 그렇기에 존재하지 않는 자식노드의 인덱스 값은 어떻게든
마지막 인덱스 값보다는 큰상황이 나올수 밖에 없다
6-2번
왼쪽 자식 노드가 마지막 노드라면
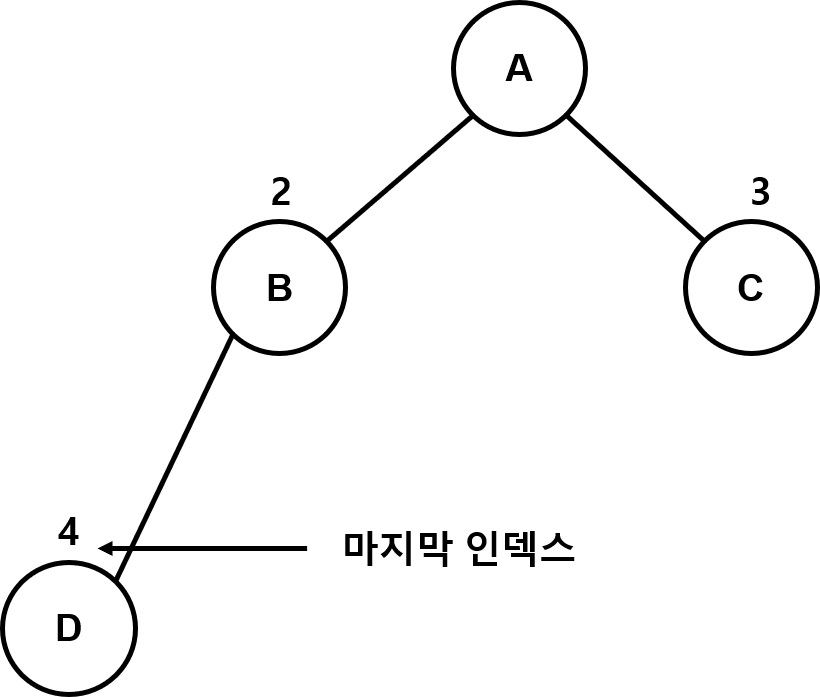
int idx값으로 2를 준다면 6-2번 코드로 진행될거다
여기서 보면 4번인덱스와 마지막 인덱스 넘버가같음을 확인할수있다
6-3번
왼쪽 자식과 오른쪽 자식중에 우선순위가 더높은 인덱스 넘버를 반환하라는 뜻이다
7번 코드
//7번
void HInsert(Heap * ph, HData data, Priority pr)
{
int idx = ph->numOfData+1;
HeapElem nelem = {pr, data};
while(idx != 1)
{
if(pr < (ph->heapArr[GetParentIDX(idx)].pr))
{
ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
idx = GetParentIDX(idx);
}
else
break;
}
ph->heapArr[idx] = nelem;
ph->numOfData += 1;
}앞서 그림에서 설명한것처럼
추가한 힙의 데이터를 힙의 마지막에 위치시킨다
동시에 값과 우선순위를 가지는데 그것을 부모노드와 계속 비교해서 자리를 조정해 간다
8번 코드
//8번
HData HDelete(Heap * ph)
{
int retData = (ph->heapArr[1]).data; // 삭제할 데이터 임시 저장
HeapElem lastElem = ph->heapArr[ph->numOfData];
int parentIdx = 1; // 루트 노드의 Index
int childIdx;
while(childIdx = GetHiPriChildIDX(ph, parentIdx))
{
if(lastElem.pr <= ph->heapArr[childIdx].pr)
break;
ph->heapArr[parentIdx] = ph->heapArr[childIdx];
parentIdx = childIdx;
}
ph->heapArr[parentIdx] = lastElem;
ph->numOfData -= 1;
return retData;
}8번 코드는 우리가 그림으로 삭제에 과정을 살펴볼때와 코드의 구현은 약간의 차이가 있다
그림에서는 먼저 첫번쨰 인덱스의 값을 삭제하고 마지막 노드를 첫번째로 옮기지만 실제로 코드를 보면 마지막 노드를
1번 노드로 옮겨서 진행하지 않는것을 확인할수 있다
HeapElem lastElem = ph->heapArr[ph->numOfData];이 코드를 보면 마지막 인덱스 정보를 따로 저장해 둔것을 확인할수있다
마치며
힙을 공부해 본것을 간단하게 정리해 봤는데 정리에 과정을 거치면서도 비선형 구조 공부가 조금씩 어려워 지고 있음을 느낀다
앞으로 남은 내용들도 천천히 제대로 이해해 나가면 좋겠다
