저번 글에서 우리는 이진 트리 순회에 필요성에 대해 알게되었고
이번 글에서 순회에 방법에 대해 공부한 내용을 정리 하겠다

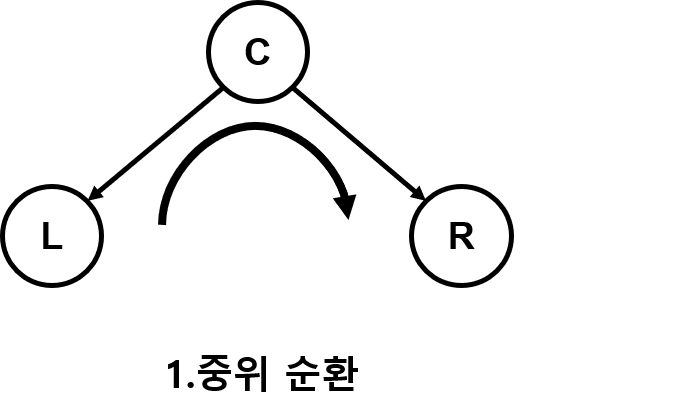
순회의 세 가지 종류

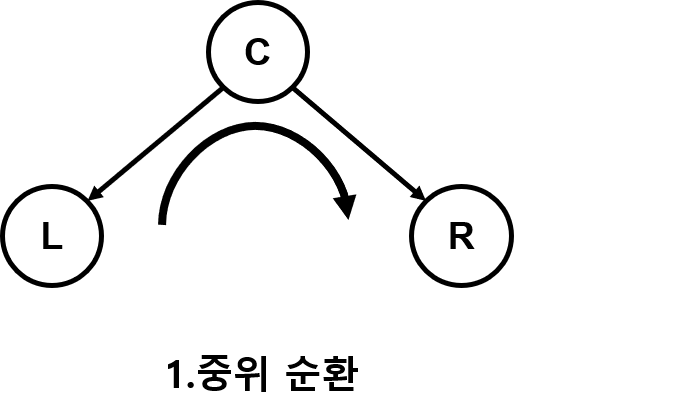
- 1.중위 순회 (루트 노드를 중간에)

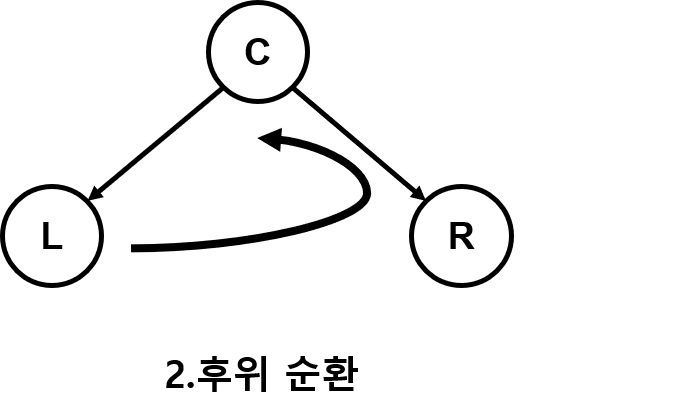
- 2.후위 순회 (루트 노드를 마지막에)

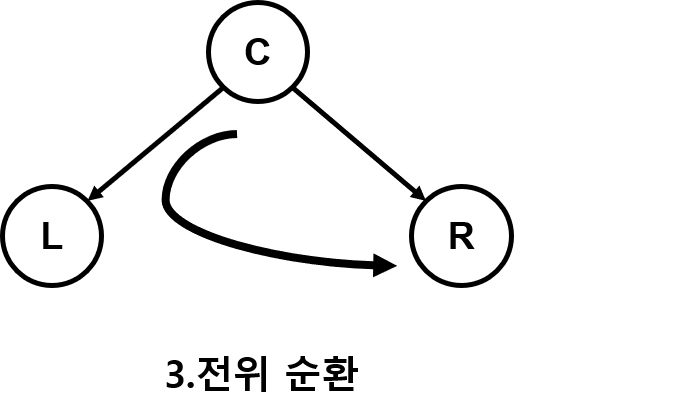
- 3.전위 순회 (루트 노드를 먼저)

위의 3가지 방식을 통해 이진 트리의 순회가 이루어 진다
그렇다면 높이가 2이상인 이진 트리는 어떻게 이루어 질까?
바로 재귀적 구현으로 가능하다

순회의 재귀적 표현

우리는 중위 순회를 기준으로 천천히 정리해 나가보자

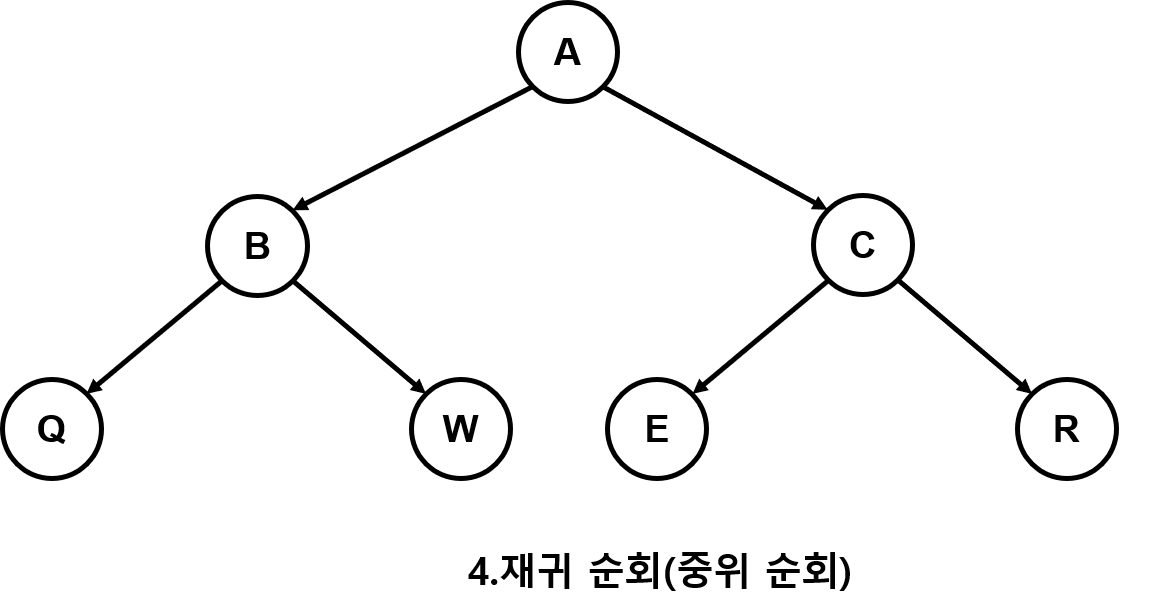
우리는 그림과 같이 다음 코드를 천천히 진행시켜 가며 재귀 순회를 정리해 보자

코드

void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
		return;

	InorderTraverse(bt->left, action);
	action(bt->data);
	InorderTraverse(bt->right, action);
}

(action함수는 루트 노드의 데이터값을 출력하는 역활을 한다)
코드의 진행 순서를 말로 풀어보자
간다한게 3가지 과정이다

1.왼쪽 서브 트리를 순회하라
2.루트 노드를 순회하라
3.오른쪽 서브 트리를 순회하라
위의 표현은 교과서 표현이니 내가 정의한 방식대로 조금 다듬자면
트리라고 생각하지 말고 1개의 노드로서 생각해보자

말로서 위 그림 트리를 접근해 보겠다

먼저 위에 코드가 진행되면 루트노드 A를 기준으로 왼쪽 노드인 B에 접근할것이다
그러면 B에 접근한 순간 재귀함수의 호출로 인해 이번에는 루트노드 B를 기준으로 왼쪽에 있는
Q에 접근할것이다 마찬가지로 Q에 접근시 재귀함수가 호출되면서 루트 노드 Q를 기준으로 왼쪽에 접근 할것이다
그순간 탈출 조건에 의해서 루트 노드 Q 에대한 함수는 끝난다 그러면 루트 노드 B의 왼쪽 진행이 끝나게 된다
그러고 나면 B에 데이터 값을 반환하고 루트 노드 B에 오른쪽인 W에 접근 하면서 ....

이런식으로 말 장난 같은 행위를 계속 해나가면 재귀함수를 이용해 이진 트리를 순회할수있다
재귀함수의 이해는 개인에 따라 재귀적 사고를 통해 익숙해 지는것을 책에서도 지향 한다
그렇기에 나는 일부 과정을 말로 정리함으로써 내가 생각한 재귀적 과정을 정리했다

마치며

정리 하는 글을 벨로그의 포스팅 하는것은 내가 배운 지식을 남에게 설명할수 있을정도로 이해하기 위해서
스스로의 공부를 위해 시작했지만 요번글을 쓰면서 참으로 글과 그림으로 남에게 설명하기가 참 어려운(내 기준)
내용도 참 많겠구나라는 생각이 들며 그때마다 내가 전달하고 이해한 내용을 부족하지만 솔직히 정리하자고
생각하게된 계기가 되었다