
- Disjoint set
- Geometry
문제
N개의 선분들이 2차원 평면상에 주어져 있다. 선분은 양 끝점의 x, y 좌표로 표현이 된다.
두 선분이 서로 만나는 경우에, 두 선분은 같은 그룹에 속한다고 정의하며, 그룹의 크기는 그 그룹에 속한 선분의 개수로 정의한다. 두 선분이 만난다는 것은 선분의 끝점을 스치듯이 만나는 경우도 포함하는 것으로 한다.
N개의 선분들이 주어졌을 때, 이 선분들은 총 몇 개의 그룹으로 되어 있을까? 또, 가장 크기가 큰 그룹에 속한 선분의 개수는 몇 개일까? 이 두 가지를 구하는 프로그램을 작성해 보자.
풀이과정
선분이 몇 개의 그룹으로 되어있고, 각 그룹에 속한 선분의 크기를 구하기 위해 Disjoint set 알고리즘을 활용하고, 두 선분이 서로 교차하는지 확인하기 위한 기하 알고리즘을 사용한다.
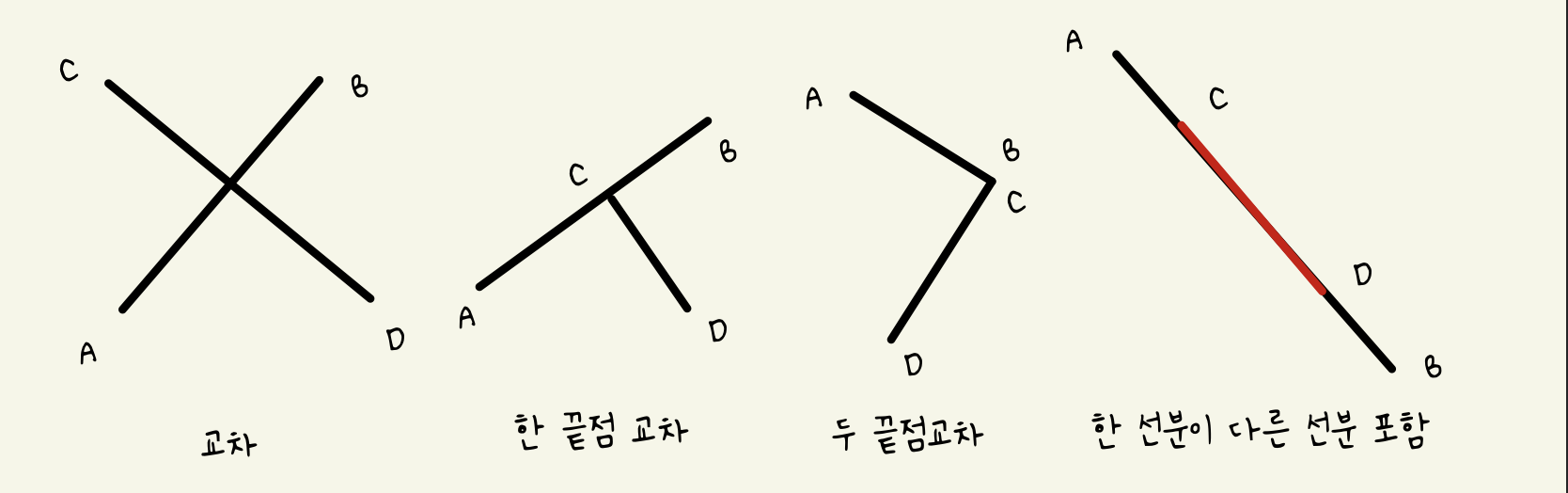
두 선분이 교차하는 경우는 위 그림과 같다.
1) 교차 : 교차의 경우에는 두 선분이 단순하게 서로 교차하는 경우이다.
2) 한 끝점 교차 : 한 선분의 끝점이 다른 선분과 만나는 경우이다.
3) 두 끝점 교차 : 두 선분의 끝점이 서로 만나는 경우이다.
4) 한 선분이 다른 선분 포함 : 두 선분이 일직선 상에 있고 교차하는 경우이다.
위 4가지 교차 케이스를 모두 포함하는 코드를 우리는 작성해야 한다. 그렇다면 두 선분이 교차한다는 사실은 어떻게 알 수 있을까? 한 선분 AB에 대하여 점 C, D가 반대편에 있고, 선분 CD에 대해 점 A, B가 반대편에 있다면 1)교차를 판별할 수 있다.
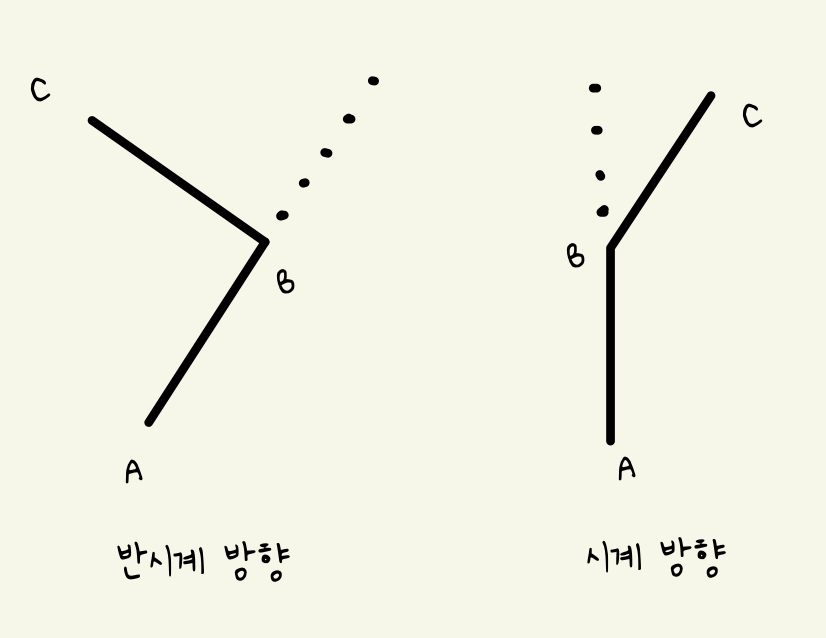
선분 AB에 대해서 한 점은 반시계 방향, 한 점은 시계 방향에 위치하면 반대편에 위치하는 것으로 판단할 수 있다. 이는 기울기를 이용하여 수식적으로 풀이할 수 있는데 반시계방향은 AB 기울기 < AC 기울기, 시계 방향은 AB 기울기 > AC 기울기인 경우로 풀이할 수 있다.
그러나 분모가 0이 되는 경우가 있으므로, 반시계 방향은 dyABdxAC < dyACdxAB, 시계 방향은 dyABdxAC > dyACdxAB로 판단한다. dyABdxAC == dyAcdxAB 인 경우는 세 점이 일직선 상에 위치하는 경우이다.
방향을 판별하는 함수 direction은 다음과 같다.
def direction(a: Point, b: Point, c: Point):
dxab = b.x - a.x
dxac = c.x - a.x
dyab = b.y - a.y
dyac = c.y - a.y
# AB 기울기 > AC 기울기
if dxab * dyac < dyab * dxac:
dir = 1
# AB 기울기 < AC 기울기
elif dxab * dyac > dyab * dxac:
dir = -1
# AB 기울기 == AC 기울기
else:
if dxab == 0 and dyab == 0:
dir == 0
if dxab * dxac < 0 or dyab * dyac < 0:
dir = -1
elif dxab * dxab + dyab * dyab >= dxac * dxac + dyac * dyac:
dir = 0
else:
dir = 1
return dirdirection 함수를 활용하면 한 선분과 두 점에 대해 위치 관계가 어떻게 되는지 판별할 수 있다. 한 선분과 두 점에 대한 direction 함수의 곱이 음수거나 0인 경우에 반대편에 위치한 것이므로, 해당 연산을 각 선분에 대해 진행하여 교차 여부를 판단할 수 있다.
def intersection(l1: Line, l2: Line):
if direction(l1.p1, l1.p2, l2.p1) * direction(l1.p1, l1.p2, l2.p2) <= 0 and \
direction(l2.p1, l2.p2, l1.p1) * direction(l2.p1, l2.p2, l1.p2) <= 0:
return True
return False교차 여부를 판단한 후에는 단순한 disjoint set 문제이다.
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = bunion_parent 함수는 disjoint set 알고리즘의 기본적인 코드로 a, b를 하나의 그룹으로 묶어준다. find_parent 함수는 x의 부모를 탐색하고, 탐색 속도를 단축하기 위해 parent 배열에 값을 저장한다.
for i in range(N):
x1, y1, x2, y2 = map(int, input().rstrip().split())
line = Line(Point(x1, y1), Point(x2, y2))
lines.append(line)
for i in range(N):
for j in range(i+1, N):
if intersection(lines[i], lines[j]):
union_parent(parent, i, j)두 선분이 교차하는 경우(intersection == True), union_parent 함수를 통해 하나의 그룹으로 묶어주면 문제를 해결할 수 있다.
코드
import sys
from collections import Counter
input = sys.stdin.readline
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
class Line:
def __init__(self, p1: Point, p2: Point):
self.p1 = p1
self.p2 = p2
def direction(a: Point, b: Point, c: Point):
dxab = b.x - a.x
dxac = c.x - a.x
dyab = b.y - a.y
dyac = c.y - a.y
# AB 기울기 > AC 기울기
if dxab * dyac < dyab * dxac:
dir = 1
# AB 기울기 < AC 기울기
elif dxab * dyac > dyab * dxac:
dir = -1
# AB 기울기 == AC 기울기
else:
if dxab == 0 and dyab == 0:
dir == 0
if dxab * dxac < 0 or dyab * dyac < 0:
dir = -1
elif dxab * dxab + dyab * dyab >= dxac * dxac + dyac * dyac:
dir = 0
else:
dir = 1
return dir
def intersection(l1: Line, l2: Line):
if direction(l1.p1, l1.p2, l2.p1) * direction(l1.p1, l1.p2, l2.p2) <= 0 and \
direction(l2.p1, l2.p2, l1.p1) * direction(l2.p1, l2.p2, l1.p2) <= 0:
return True
return False
# N개의 선분
N = int(input())
lines = []
parent = [i for i in range(N)]
for i in range(N):
x1, y1, x2, y2 = map(int, input().rstrip().split())
line = Line(Point(x1, y1), Point(x2, y2))
lines.append(line)
for i in range(N):
for j in range(i+1, N):
if intersection(lines[i], lines[j]):
union_parent(parent, i, j)
parent = [find_parent(parent, x) for x in parent]
cnt = Counter(parent)
print(len(cnt)) # 그룹의 수
print(max(cnt.values())) # 가장 크기가 큰 그룹에 속하는 선분의 개수
