자료구조
- 여러 데이터들의 묶음을 어떻게 저장할 것이고, 사용할 것인지 정의한 것이다.
- 무수한 상황들을 효율적으로 대응할 수 있는 여러 방법에 대한 연구로부터 탄생
- 많은 자료구조를 알아두어야 어떠한 상황이 닥쳤을 때 적합한 자료구조를 사용하여 문제를 해결할 수 있다.
Stack
- 자료(data)를 쌓는 자료구조
- Stack 자료구조의 특성은 입출이 하나인 제한적 접근에 있다. 이런 Stack 자료구조의 정책을 LIFO(Last In First Out) 혹은 FILO(First In Last Out)이라고 부르기도 한다.
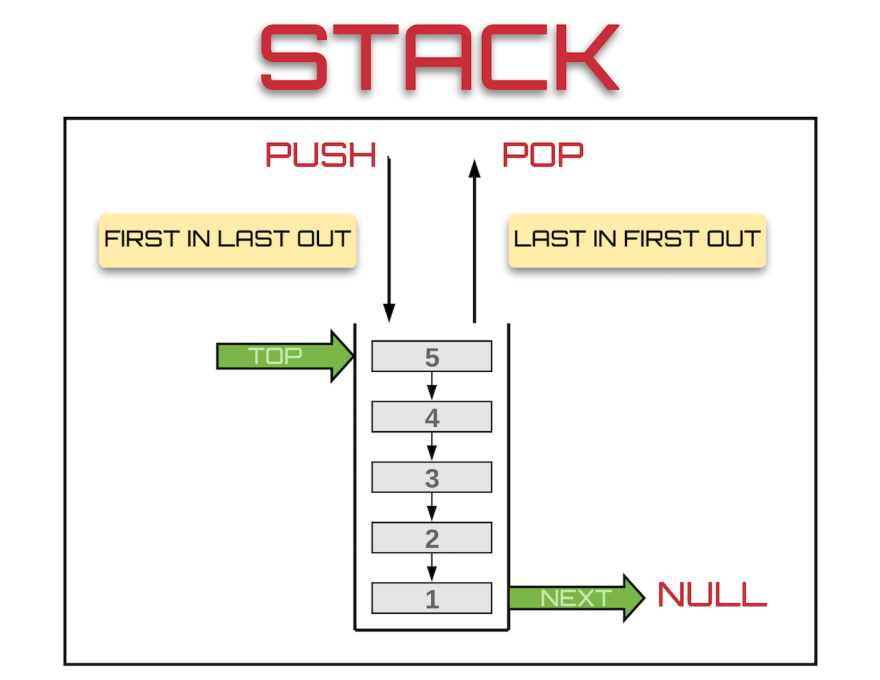
*https://dev.to/theoutlander/implementing-the-stack-data-structure-in-javascript-4164 - stack의 실사용 예제로는 브라우저의 뒤로가기 앞으로가기가 있다. (두개의 스텍을 이용)
Queue
- Stack과 반대되는 개념으로, 먼저 들어간 자료(data)가 먼저 나오는 FIFO(First In First Out) 혹은 LILO(Last In Last Out) 의 특성을 가지고 있는 자료구조이다.
- Queue는 자료(data)가 입력된 순서대로 처리해야 할 필요가 있는 상황에서 사용된다.
- Queue의 실사용 예제로는 프린터가 있다.
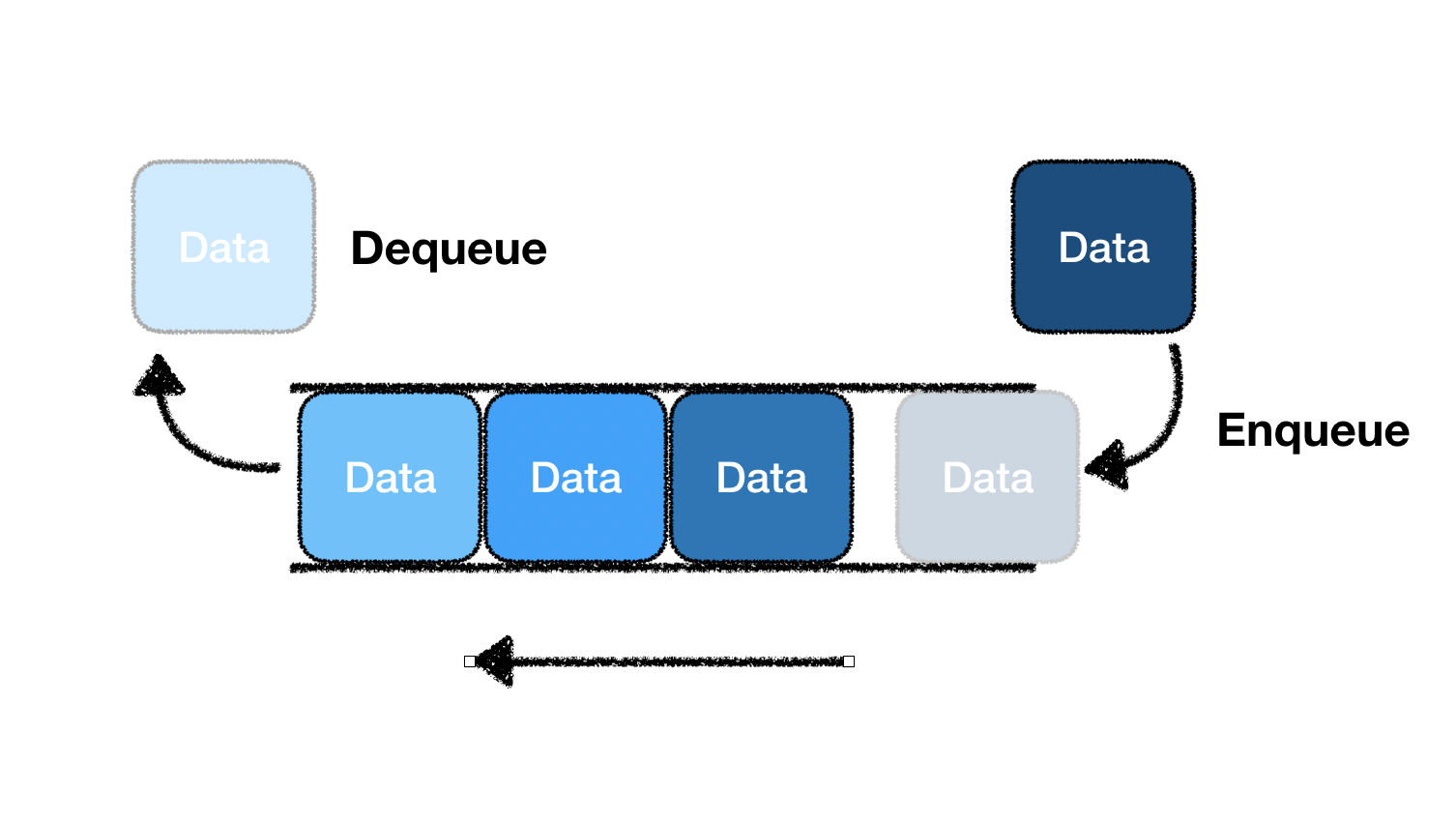
*https://helloworldjavascript.net/pages/282-data-structures.html
Graph
-
여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조.
-
서로 다른 점들이 직접적인 관계를 가지고 있다면 바로 이어주는 선이 존재하고, 간접적인 관계를 가지고 있다면 다른 여러 점을 거쳐서 이어지는 선이 존재할 수 있다. 여기서 이야기 하는 점은 그래프에서는 정점(vertex)이라고 표현하고, 선은 간선(edge) 이라고 표현한다.
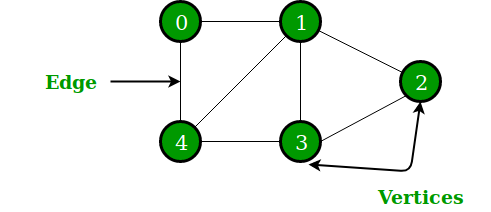
*https://www.geeksforgeeks.org/ -
포털 사이트의 검색 엔진, SNS, 네비게이션 (길찾기) 등에서 사용하는 자료구조가 바로 그래프이다. 세 가지 모두 여러 개의 정점을 가지고 있으며, 서로 관계가 있는 정점은 간선으로 이어져 있다.
-
무향그래프(undirected graph): 내비게이션은 무향 그래프 이다. 서울에서 부산으로 갈 수 있듯, 반대로 부산에서 서울로 가는것도 가능하다. 하지만 단방향(directed) 그래프로 구현 된다면 서울에서 부산을 갈 수 있지만, 부산에서 서울로 가는 것은 불가능하다(혹은 그 반대). 만약 두 지점이 일방통행 도로로 이어져 있다면 단방향인 간선으로 표현할 수 있다.
-
진입차수(in-degree) / 진출차수(out-degree): 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타냅니다.
-
인접(adjacency): 두 정점간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점이라 부른다.
-
자기 루프(self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다 라고 표현한다. 다른 정점을 거치지 않는다는 것이 특징.
-
사이클(cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다. 내비게이션을 예로 들면 서울 —> 대전 —> 부산 —> 서울 로 이동이 가능하므로 사이클이 존재하는 그래프 이다.
인접행렬
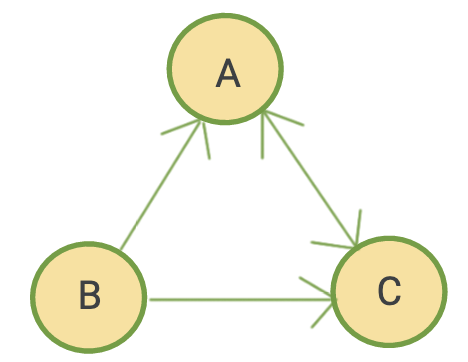
- 두 정점을 바로 이어 주는 간선이 있다면 이 두 정점은 인접하다고 이야기한다. 인접 행렬은 정점들간의 인접함을 표시해 주는 행렬으로 2차원 배열의 모습을 가지고 있습니다. 만약 A라는 정점과 B라는 정점이 이어져 있다면 1, 이어져 있지 않다면 0으로 표시하는 일종의 표와 같은 모습입니다. 만약 가중치 그래프라면 1 대신 관계에서 의미 있는 값(내비게이션에선 거리)을 저장합니다. 위 그래프를 인접 행렬로 표현했을 때의 모습은 다음과 같습니다
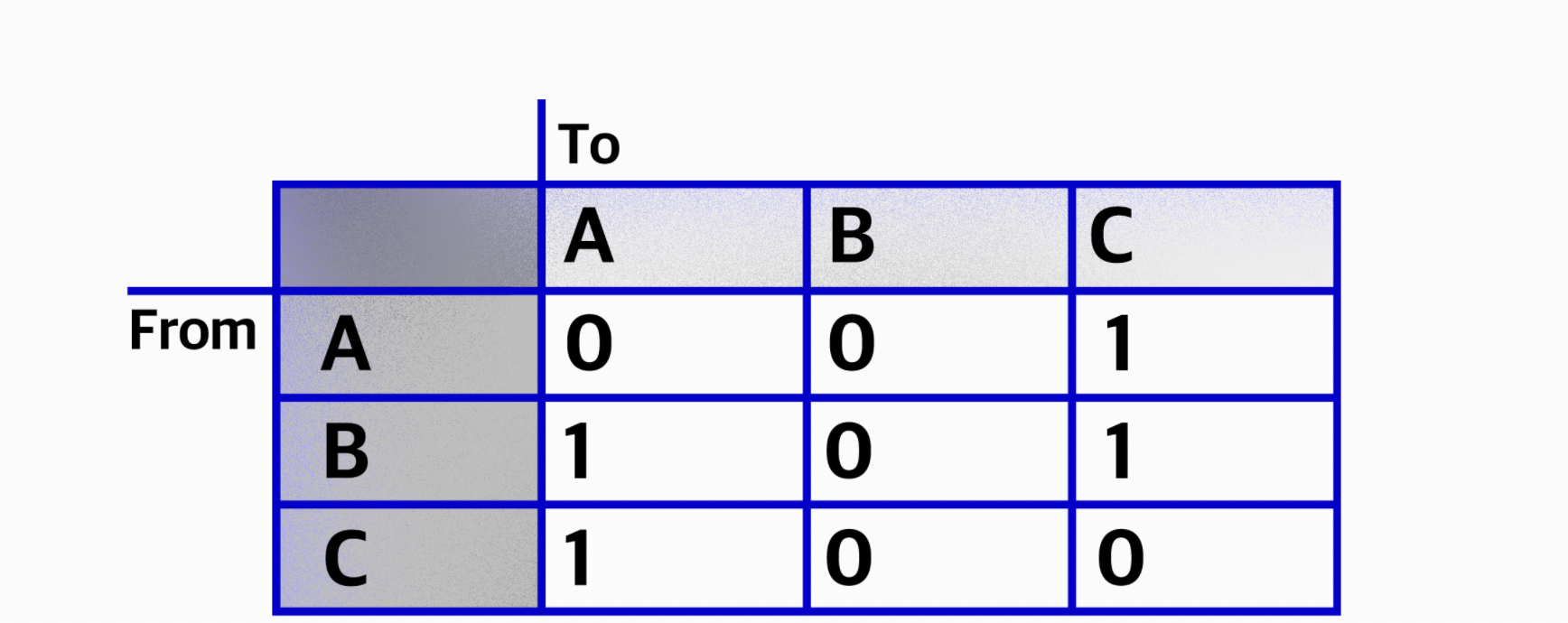
인접행렬의 용도
- 한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이하다.(예를 들어, A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0 번째 줄의 1 번째 열에 어떤 값이 저장되어있는지 바로 확인할 수 있다.)
- 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용된다
인접 리스트
- 각 정점이 어떤 정점과 인접한지 리스트의 형태로 볼 수 있는 표현 방식
- 각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트에는 자신과 인접한 다른 정점들이 담겨 있다.
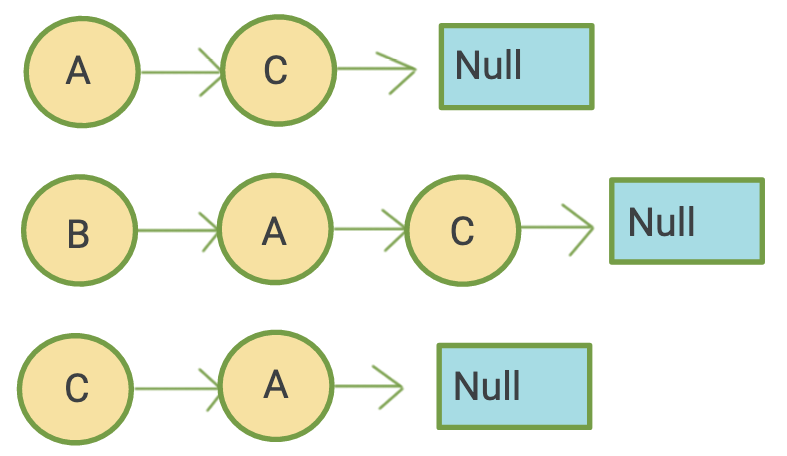
인접 리스트의 용도
- 인접 행렬은 연결 가능한 모든 경우의 수를 저장한다.
(서로 인접하지 않다면 0을, 인접하다면 1을 저장하기 때문에 메모리를 많이 차지하게 된다) - 메모리를 효율적으로 사용하고 싶다면 인접 행렬 대신 인접 리스트를 사용


