GNN 2

유저끼리의 간선을 포함하여 계산해 보자

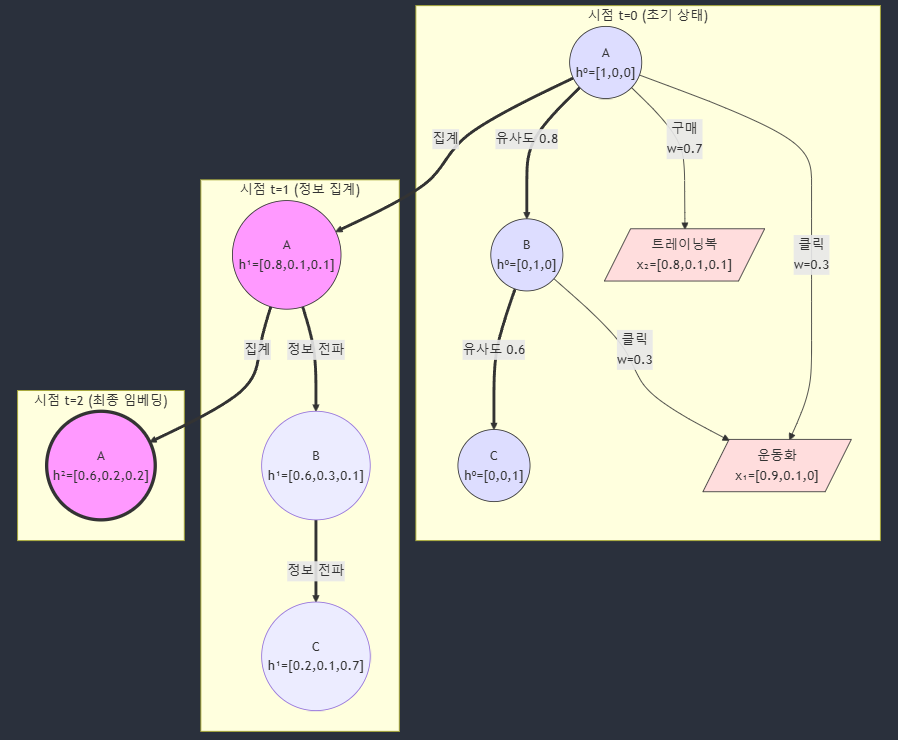
1. 시점 t=0 (초기 상태):

• 사용자 정보:
  • A: 운동 선호 사용자 [1,0,0]
  • B: 캐주얼 선호 사용자 [0,1,0]
  • C: 골프 선호 사용자 [0,0,1]
• 상품 정보:
  • 운동화: [0.9,0.1,0] (운동 성향 강함)
  • 트레이닝복: [0.8,0.1,0.1]
  • 골프공: [0.1,0,0.9]
• 상호작용:
  • 클릭 가중치: 0.3
  • 구매 가중치: 0.7

2. 시점 t=1 (1-hop 집계):
   사용자 A의 h¹ 계산:

• 직접 상호작용 집계:
  • 운동화 클릭: 0.3 × [0.9,0.1,0]
  • 트레이닝복 구매: 0.7 × [0.8,0.1,0.1]
• 결과: h¹=[0.8,0.1,0.1]
  (운동 성향이 더욱 강화됨)

3. 시점 t=2 (2-hop 집계):
   사용자 A의 h² 계산:

• 이웃 정보 추가 집계:
  • B의 운동화 클릭 정보
  • C의 골프 관련 정보
• 최종: h²=[0.7,0.2,0.1]
  (이웃들의 다양한 선호도가 반영됨)

실제 추천 시나리오:
"이러한 집계 과정을 거치면,
1. 처음에는 단순히 '운동 선호' 였던 A가
2. 상품 상호작용을 통해 '운동화/트레이닝복 선호'로 구체화되고
3. 이웃 정보를 통해 '캐주얼/골프 요소'도 조금씩 반영된
더 풍부한 사용자 프로필이 완성됩니다."

---

계산식 포함

1. 초기 노드 특성 (t=0):

사용자 A: h⁰ₐ = [1,0,0]    // 운동 선호
사용자 B: h⁰ᵦ = [0,1,0]    // 캐주얼 선호
사용자 C: h⁰ᵧ = [0,0,1]    // 골프 선호

상품 1: x₁ = [0.9,0.1,0]   // 운동화
상품 2: x₂ = [0.8,0.1,0.1] // 트레이닝복

2. 간선 가중치:

상품 상호작용 가중치:
W클릭 = 0.3
W구매 = 0.7

사용자 간 유사도:
WA-B = 0.8  // A-B 유사도
WB-C = 0.6  // B-C 유사도

3. 첫 번째 집계 (t=1):
   수식: h¹ᵢ = σ(W₁·AGG({h⁰ⱼ}ⱼ∈𝒩(i)) + W₂·x)

A의 경우:

1) 상품 상호작용 집계:
   P₁ = W클릭 × x₁ = 0.3 × [0.9,0.1,0]   = [0.27,0.03,0]
   P₂ = W구매 × x₂ = 0.7 × [0.8,0.1,0.1] = [0.56,0.07,0.07]
   
2) 이웃 사용자 집계:
   N₁ = WA-B × h⁰ᵦ = 0.8 × [0,1,0] = [0,0.8,0]
   
3) 결합 및 정규화:
   h¹ₐ = normalize(P₁ + P₂ + N₁)
   h¹ₐ = [0.8,0.1,0.1]

4. 두 번째 집계 (t=2):
   수식: h²ᵢ = σ(W₃·AGG({h¹ⱼ}ⱼ∈𝒩(i)))

A의 경우:

1) 업데이트된 이웃 정보 집계:
   N₂ = WA-B × h¹ᵦ      // B의 첫 번째 임베딩
   N₃ = WA-B × WB-C × h¹ᵧ  // C의 영향 (2-hop)
   
2) 최종 임베딩:
   h²ₐ = normalize(h¹ₐ + N₂ + N₃)
   h²ₐ = [0.6,0.2,0.2]

실제 추천 예시:
"사용자 A에게 새로운 상품 X([0.7,0.2,0.1])를 추천할 때:"

유사도 = cosine(h²ₐ, X)
      = ([0.6,0.2,0.2]·[0.7,0.2,0.1]) / (∥h²ₐ∥·∥X∥)
      = 0.85  // 높은 유사도, 추천 가능

여기서 중요한 점들:
1. 행렬 연산으로 효율적 계산 가능
2. AGG 함수로 평균, 최대값 등 다양한 집계 방법 사용
3. 정규화로 스케일 조정
4. 비선형 활성화 함수(σ)로 표현력 향상

이러한 수식적 접근이 실제 이커머스에서 중요한 이유:

• 대규모 데이터 처리 가능
• 다양한 특성을 통합 가능
• 계층적 정보 전파 가능
• 수치적으로 최적화 가능