Girvan-Newman 알고리즘 (하양식 방법)

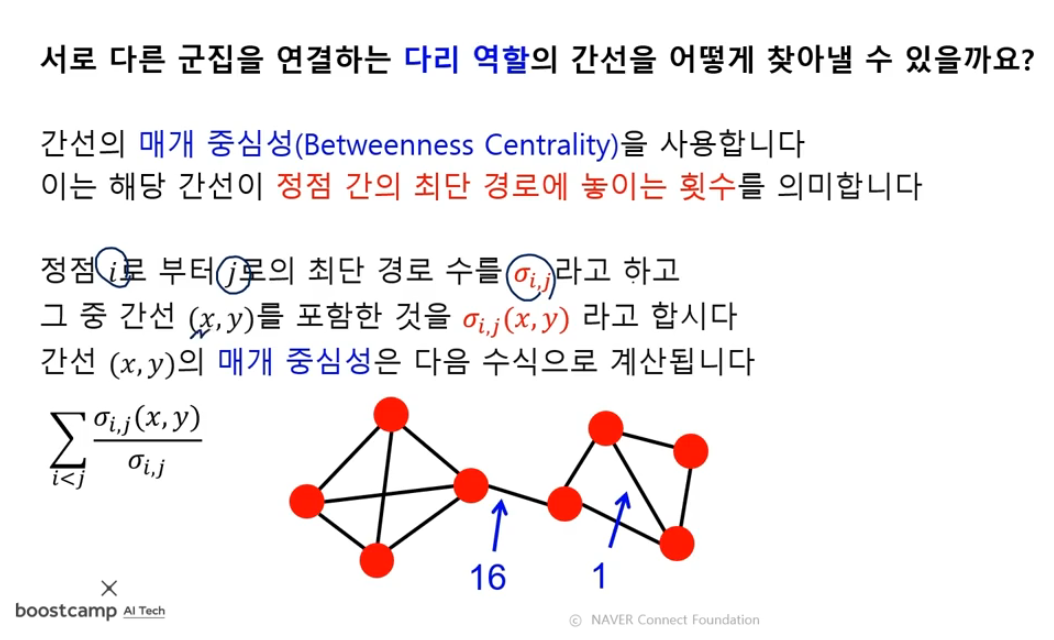
매개 중심성 계산 공식 쉽게 설명

• Σ (시그마)는 모든 경우의 합을 구한다는 의미입니다.
• i<j는 모든 노드 쌍을 한 번씩만 계산한다는 뜻입니다.

더 쉽게 풀어서 설명하면:

σᵢⱼ(x,y) : i에서 j로 가는 최단 경로 중 간선 (x,y)를 지나는 경로의 수
σᵢⱼ : i에서 j로 가는 최단 경로의 총 개수

실제 예시

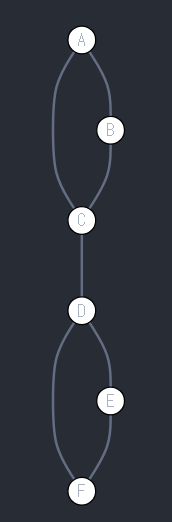
이 단순화된 그래프에서 매개 중심성을 계산해보겠습니다:

1️⃣ C-D 간선의 매개 중심성 계산:

1단계: 모든 노드 쌍(i<j) 나열:

A→D, A→E, A→F
B→D, B→E, B→F
C→E, C→F

2단계: 각 경로별 계산

A→D:
- 총 경로 수 = 1 (A→C→D)
- C-D 통과 경로 수 = 1
- 점수 = 1/1 = 1

A→E:
- 총 경로 수 = 1 (A→C→D→E)
- C-D 통과 경로 수 = 1
- 점수 = 1/1 = 1

[나머지 경로들도 같은 방식으로 계산]

3단계: 합산

C-D의 매개 중심성 = 8.0

2️⃣ D-E 간선의 매개 중심성:

A→E: 1/1 = 1
B→E: 1/1 = 1
C→E: 1/1 = 1
D→F: 1/2 = 0.5 (D→F 직접 가는 경로 존재)

D-E의 매개 중심성 = 3.5

3️⃣ 모든 간선의 매개 중심성 결과:

A-B: 1.0
A-C: 2.0
B-C: 1.0
C-D: 8.0
D-E: 3.5
D-F: 3.5
E-F: 2.0

이렇게 보면 더 명확하게 각 연결의 중요도를 파악할 수 있습니다. C-D 간선이 가장 높은 매개 중심성을 가지고 있어, 이 연결이 네트워크에서 가장 중요한 다리 역할을 한다는 것을 알 수 있습니다.