- KNN의 기본 개념
KNN은 새로운 데이터 포인트가 들어왔을 때, 가장 가까운 K개의 이웃들의 다수결로 분류하는 알고리즘입니다. 마치 "새로운 동네로 이사왔을 때, 가장 가까운 이웃 K명의 성향을 보고 그 동네의 특성을 파악하는 것"과 같습니다.
- 거리 계산 방법
가장 일반적으로 사용되는 유클리디안 거리를 예시로 설명하겠습니다.
두 점 A(x₁, y₁)와 B(x₂, y₂) 사이의 거리:
d = √[(x₁-x₂)² + (y₁-y₂)²]
- 실제 예시
상황: 새로운 과일이 들어왔을 때 사과인지 배인지 분류하는 문제
- 특성 1: 무게(g)
- 특성 2: 당도(brix)
기존 데이터:
과일1(사과): (120g, 13brix)
과일2(사과): (130g, 12brix)
과일3(배): (180g, 11brix)
과일4(배): (170g, 10brix)
과일5(사과): (125g, 14brix)새로운 과일 X: (140g, 11brix)가 들어왔을 때, K=3이라면:
1) 거리 계산:
- X~과일1 거리 = √[(140-120)² + (11-13)²] = 20.4
- X~과일2 거리 = √[(140-130)² + (11-12)²] = 10.0
- X~과일3 거리 = √[(140-180)² + (11-11)²] = 40.0
- X~과일4 거리 = √[(140-170)² + (11-10)²] = 30.0
- X~과일5 거리 = √[(140-125)² + (11-14)²] = 15.8
2) 가장 가까운 3개 선택:
- 1위: 과일2(사과) - 10.0
- 2위: 과일5(사과) - 15.8
- 3위: 과일1(사과) - 20.4
3) 다수결 판정:
가장 가까운 3개 중 사과가 3개, 배가 0개이므로 새로운 과일 X는 '사과'로 분류됩니다.
- K값 선택의 중요성
K=1일 경우: 과일2(사과)만 보고 판단 → 노이즈에 민감
K=5일 경우: 모든 데이터 사용 → 과대적합 위험
이처럼 K값은 데이터의 특성과 노이즈를 고려해 적절히 선택해야 합니다. 일반적으로 데이터 개수의 제곱근을 K값으로 사용하는 것이 좋습니다.
- 장단점
장점:
- 이해하기 쉽고 구현이 간단함
- 새로운 데이터가 들어와도 재학습 필요 없음
- 다중 분류 문제에도 적용 가능
단점:
- 계산 비용이 높음 (모든 데이터와의 거리 계산 필요)
- 데이터의 스케일에 민감
- 차원이 높아지면 성능 저하 (차원의 저주)
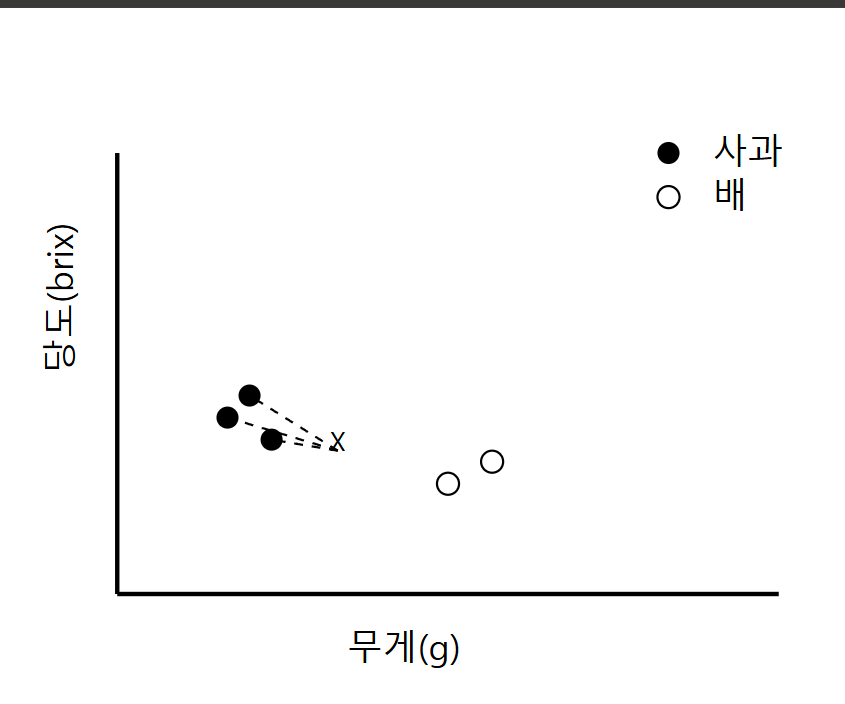
이 그래프에서:
- 검은 점: 사과
- 흰 점: 배
- X: 새로운 데이터 포인트
- 점선: K=3일 때 가장 가까운 이웃까지의 거리
그래프를 보면 새로운 데이터 포인트 X는 사과 데이터(검은 점)들과 더 가깝기 때문에 사과로 분류됨을 시각적으로 확인할 수 있습니다.
KNN 알고리즘의 핵심은 "비슷한 특성을 가진 데이터는 비슷한 범주에 속할 것이다"라는 단순하면서도 강력한 가정에 기반합니다. 마치 우리가 새로운 사람을 만났을 때, 그 사람과 가장 비슷한 성향을 가진 지인들을 떠올려 그 사람의 성향을 추측하는 것과 같은 원리입니다.
