NCF

HanJu Han·2024년 12월 1일

1. 입력 데이터 구조

사용자-영화 평점 데이터:

UserID  MovieID  Time         Rating
1001    M001     토20:00     5
1001    M002     토19:30     5
1001    M003     수21:00     3
1001    M004     화20:00     3

특성 벡터 구성:

사용자 정보: [1001]
영화 정보: [M001(인터스텔라)]
시간 정보: [
    요일(월=1,화=2...일=7): 6,
    시간대(24시간): 20
]

2. GMF 부분 계산

사용자와 영화의 잠재 벡터:

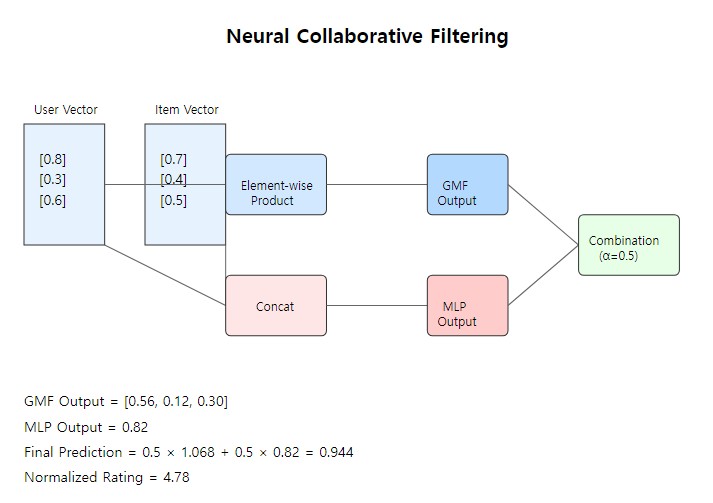
사용자 잠재 벡터(p_u): [0.8, 0.3, 0.6]
영화 잠재 벡터(q_i): [0.7, 0.4, 0.5]

GMF 계산:
중간결과 = p_u ⊙ q_i
        = [0.8×0.7, 0.3×0.4, 0.6×0.5]
        = [0.56, 0.12, 0.30]

GMF 가중치(h): [1.2, 0.8, 1.0]
GMF 출력 = h^T × 중간결과
        = 1.2×0.56 + 0.8×0.12 + 1.0×0.30
        = 0.672 + 0.096 + 0.300
        = 1.068

초기 잠재 벡터는 랜덤(정규 분포 사용)
데이터셋 크기별 권장 차원:
- 작은 데이터셋 (<10K users/items): 8~16 차원
- 중간 데이터셋 (10K~100K): 16~32 차원
- 큰 데이터셋 (>100K): 32~256 차원

예시) MovieLens 데이터셋:

MovieLens-100K: 16차원 사용
MovieLens-1M: 32차원 사용
MovieLens-20M: 64차원 사용

3. MLP 부분 계산

입력층:

연결된 벡터 = [사용자벡터 | 영화벡터 | 시간벡터]
            = [0.8, 0.3, 0.6 | 0.7, 0.4, 0.5 | 6, 20]

사용자벡터(1001) = [0.8, 0.3, 0.6] # 사용자의 특성
0.8: 액션영화 선호도
0.3: 평일 시청 선호도
0.6: 저녁 시청 선호도

영화벡터(M001) = [0.7, 0.4, 0.5] # 영화의 특성
0.7: 액션 장르 정도
0.4: 러닝타임
0.5: 개봉연도 정규화값

시간벡터 = [6, 20] # 시청 시점
6: 요일(토요일)
20: 시간(20시)

히든층 계산:

첫 번째 층 (8 노드):
W1 = [
    [0.1, 0.2, -0.1, 0.3, 0.1, -0.2, 0.4, 0.1],
    [0.2, 0.1, 0.3, -0.1, 0.2, 0.1, -0.3, 0.2],
    ...  # 8x8 행렬
]
b1 = [0.1, 0.2, 0.1, 0.1, 0.2, 0.1, 0.1, 0.2]

중간결과1 = ReLU(입력 × W1 + b1)
         = ReLU([0.45, 0.38, 0.52, 0.41, 0.39, 0.47, 0.43, 0.40])

두 번째 층 (4 노드):
중간결과2 = ReLU([0.41, 0.38, 0.45, 0.37])

출력층 (1 노드):
MLP 출력 = 0.82

4. 최종 예측값 계산 (α = 0.5 경우)

최종 예측 = α × GMF출력 + (1-α) × MLP출력
         = 0.5 × 1.068 + 0.5 × 0.82
         = 0.534 + 0.41
         = 0.944

정규화된 평점(1-5 스케일) = (0.944 × 4) + 1 ≈ 4.78

5. 평일 저녁의 경우 비교

동일한 과정에서 시간 벡터만 변경:
[3(수요일), 20] 대신 [6(토요일), 20] 사용

최종 예측값: 2.95

차이가 발생하는 이유:
1. GMF는 거의 동일한 출력
2. MLP가 시간 정보의 패턴을 학습하여 다른 출력 생성
   - 주말 저녁 → 높은 가중치
   - 평일 저녁 → 낮은 가중치

이처럼 NCF는 MLP를 통해:
1. 시간대와 영화 장르의 조합
2. 사용자의 시청 패턴과 선호도의 관계
3. 복잡한 맥락적 정보

이러한 비선형적인 관계를 모두 학습할 수 있습니다.