Post-Quantization (양자화)

포스트 퀀타이제이션(Post-Quantization)은 딥러닝 모델의 크기를 줄이고 추론 속도를 높이기 위해 사용되는 기술입니다.

1. 가중치 표현 변환:

   • 원래 모델은 32비트 부동소수점(floating-point)으로 가중치를 표현합니다.
   • 양자화 후에는 2비트 부호있는 정수(signed int)로 가중치를 표현합니다.

2. 양자화 과정:

   • Zero Point와 Scale을 사용하여 부동소수점 값을 정수로 변환합니다.
   • Zero Point: 0에 해당하는 양자화된 값
   • Scale: 양자화 단계 크기

3. 수식:
   양자화된 가중치 = round((원래 가중치 / Scale) + Zero Point)

4. 역양자화 과정:

   • 추론 시 사용할 때는 양자화된 가중치를 다시 부동소수점으로 변환합니다.
   • 수식: 복원된 가중치 = (양자화된 가중치 - Zero Point) * Scale

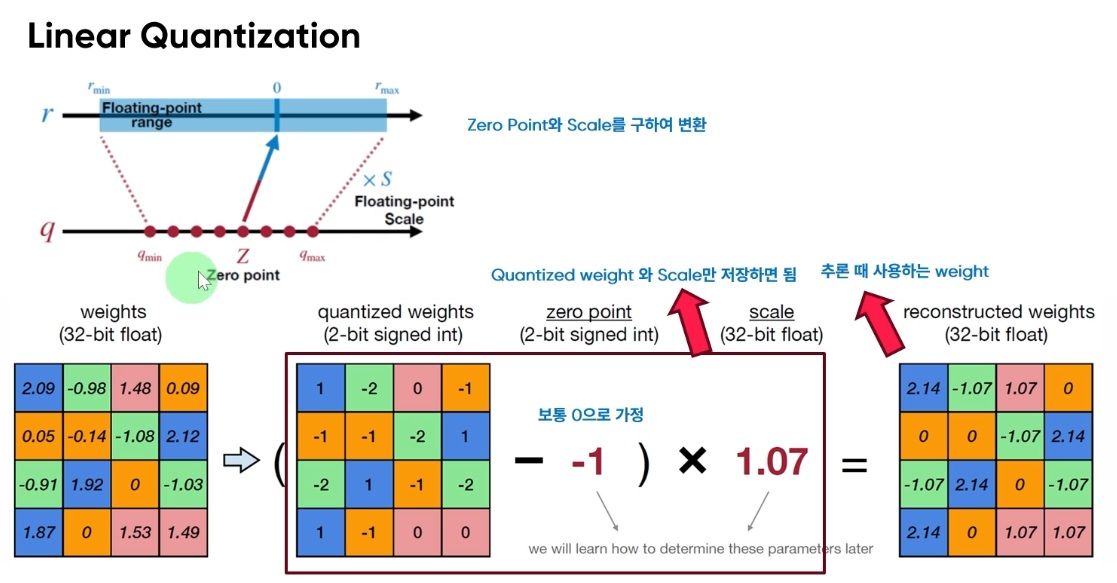
5. 이미지 예시 설명:

   • 원래 가중치: 32비트 부동소수점 행렬
   • 양자화된 가중치: 2비트 부호있는 정수 행렬 (-2, -1, 0, 1)
   • Zero Point: -1 (이미지의 예시)
   • Scale: 1.07 (이미지의 예시)

6. 장점:

   • 모델 크기 감소: 32비트에서 2비트로 압축
   • 메모리 사용량 감소
   • 추론 속도 향상
   • 에너지 효율성 증가

7. 주의사항:

   • 정밀도 손실이 발생할 수 있으므로, 모델의 성능을 유지하면서 적절한 비트 수를 선택해야 합니다.
   • Zero Point와 Scale 파라미터의 최적화가 중요합니다.

포스트 퀀타이제이션은 학습된 모델에 적용되는 기술로, 모델의 구조나 학습 과정을 변경하지 않고도 효율성을 높일 수 있는 방법입니다. 특히 모바일이나 임베디드 기기에서 딥러닝 모델을 실행할 때 유용하게 사용됩니다.

예시

이미지에서 주어진 정보:
- Scale (S) = 1.07
- Zero point (Z) = -1
- 양자화 비트 = 2비트 (-2, -1, 0, 1)

원본 가중치 중 하나를 선택해 계산해보겠습니다. 왼쪽 상단의 2.09를 사용하겠습니다.

1. 양자화 과정:
   공식: q = round((r / S) + Z), 여기서 r은 원본 가중치, q는 양자화된 가중치입니다.
   
   q = round((2.09 / 1.07) + (-1))
   q = round(1.9533 + (-1))
   q = round(0.9533)
   q = 1

   따라서 2.09는 양자화되어 1이 됩니다.

2. 역양자화 과정 (복원):
   공식: r' = (q - Z) * S, 여기서 r'은 복원된 가중치입니다.
   
   r' = (1 - (-1)) * 1.07
   r' = 2 * 1.07
   r' = 2.14

이 과정을 통해 원래의 2.09가 양자화되어 1이 되고, 
다시 역양자화되어 2.14로 복원되는 것을 볼 수 있습니다.

다른 예시로, -0.98을 양자화해보겠습니다:

1. 양자화:
   q = round((-0.98 / 1.07) + (-1))
   q = round(-0.9159 + (-1))
   q = round(-1.9159)
   q = -2

2. 역양자화:
   r' = (-2 - (-1)) * 1.07
   r' = -1 * 1.07
   r' = -1.07

이렇게 -0.98이 -2로 양자화되고, 다시 -1.07로 복원됩니다.

이 과정을 모든 원본 가중치에 적용하면 이미지에서 보이는 결과를 얻을 수 있습니다. 
양자화 과정에서 약간의 정보 손실이 발생하지만, 데이터 크기를 크게 줄일 수 있습니다.
32비트 부동소수점에서 2비트 정수로 변환됨으로써 메모리 사용량이 1/16로 감소하게 됩니다.