경로 기반 접근법

수식을 직관적으로 이해해보겠습니다:

1. 기본 개념 설명:

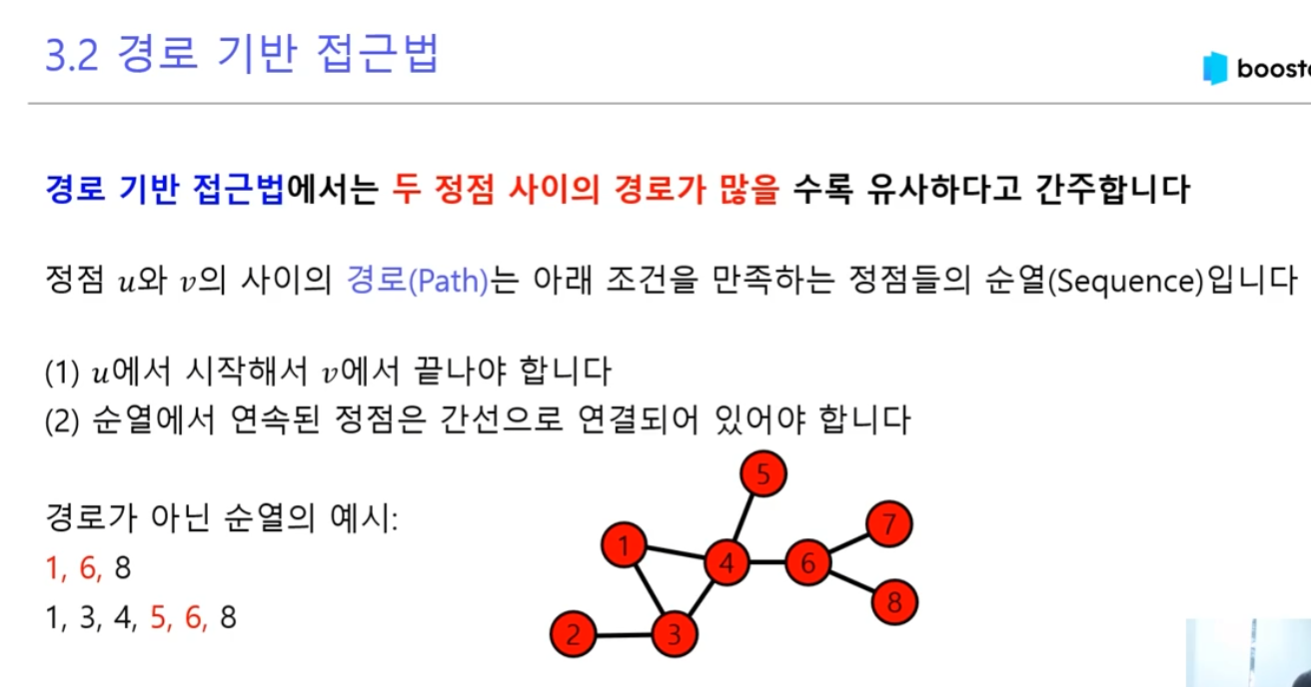
   • 두 정점(u,v) 사이의 경로 중 거리가 k인 것을 A^k_{u,v}로 표현합니다
   • 예를 들어, A가 다음과 같은 소셜 네트워크를 나타낸다고 가정해봅시다:
     • 철수(1) - 영희(2) - 민수(3) - 지영(4)

2. 실제 예시로 이해하기:

   • A^1 (거리가 1인 직접 연결):

     • 철수-영희: A^1_{1,2} = 1
     • 영희-민수: A^1_{2,3} = 1
     • 민수-지영: A^1_{3,4} = 1
     • 직접 연결되지 않은 경우: A^1_{1,3} = 0

   • A^2 (거리가 2인 연결):

     • 철수-민수: A^2_{1,3} = 1 (철수→영희→민수)
     • 영희-지영: A^2_{2,4} = 1 (영희→민수→지영)

3. 수식 해석:

L = Σ ||z_u^T z_v - A^k_{u,v}||^2
  (u,v)∈V×V

이 수식은:

• z_u^T z_v: 두 노드 사이의 임베딩 유사도
• A^k_{u,v}: 실제 k-거리 관계
• 이 둘의 차이를 최소화하려는 것이 목적

4. 직관적 이해:
   예를 들어 철수와 영희가 친구라면:

• z철수^T z영희 ≈ 1 이 되도록
• z철수^T z민수 ≈ 0 이 되도록 학습

5. 학습의 결과:

• k=1인 직접 연결된 노드들은 임베딩 공간에서 가깝게 위치
• k=2인 간접 연결된 노드들은 적당한 거리를 유지
• 연결되지 않은 노드들은 멀리 위치

이러한 방식으로 그래프의 구조적 특성을 보존하면서 각 노드의 임베딩을 학습하게 됩니다.

---

인접성 기반 접근법과의 차이

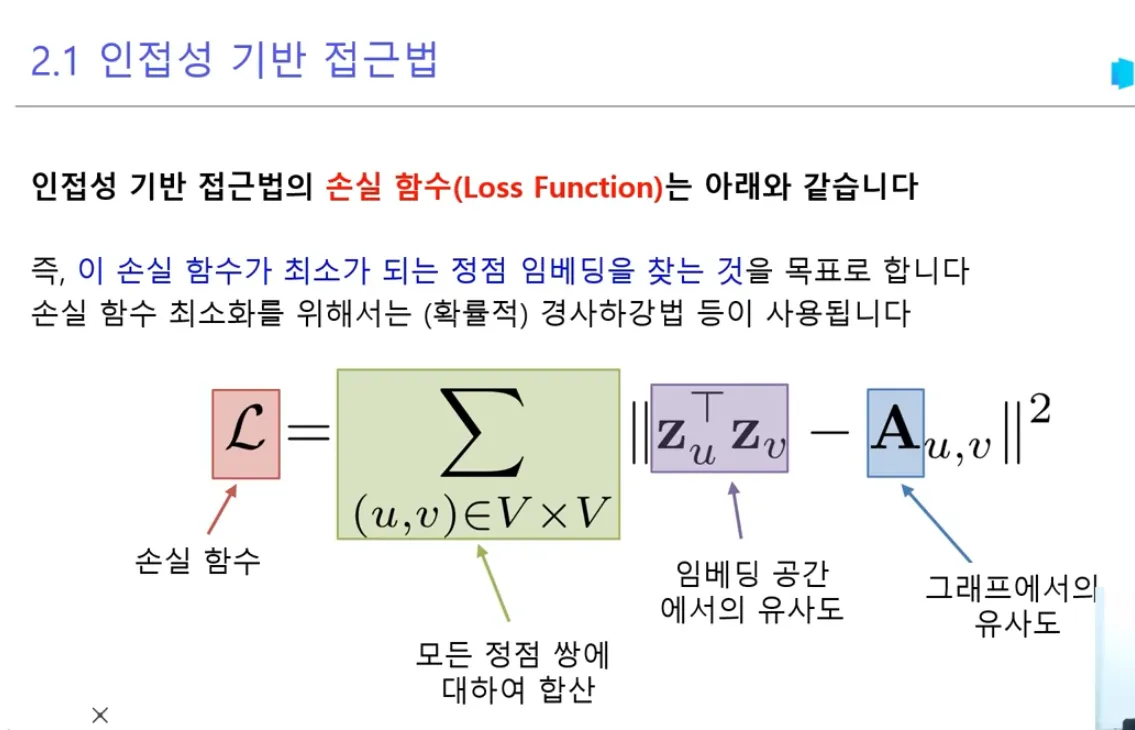
1. 기본 구조는 동일:

L = Σ ||z_u^T z_v - A_{u,v}||^2
  (u,v)∈V×V

2. 핵심적인 차이점:

• 인접성 기반(2.1)에서는 A_{u,v}가 직접 연결 여부만 표현

  • A_{u,v} = 1: 직접 연결된 노드
  • A_{u,v} = 0: 직접 연결되지 않은 노드

• 경로 기반(3.2)에서는 A^k_{u,v}가 k-거리 관계를 표현

  • A^k_{u,v} = 1: k단계 거리로 연결된 노드
  • A^k_{u,v} = 0: k단계 거리로 연결되지 않은 노드

3. 실제 예시로 비교:
   소셜 네트워크에서 철수-영희-민수가 있다고 할 때:

인접성 기반:

• 철수-영희: A_{1,2} = 1 (직접 연결)
• 철수-민수: A_{1,3} = 0 (직접 연결 아님)

경로 기반:

• 철수-영희: A^1_{1,2} = 1 (1단계 거리)
• 철수-민수: A^2_{1,3} = 1 (2단계 거리)

4. 임베딩 학습의 차이:

인접성 기반:

• 직접 연결된 노드들만 가깝게 위치
• 나머지는 모두 멀리 위치하도록 학습

경로 기반:

• k에 따라 다양한 거리 관계 반영
• 경로 길이에 따른 단계적 거리 유지

5. 장단점 비교:

인접성 기반:

• 장점: 단순하고 계산이 빠름
• 단점: 간접적 관계 정보 손실

경로 기반:

• 장점: 더 풍부한 구조적 정보 포착
• 단점: 계산 비용이 더 큼

결론적으로, 경로 기반 접근법은 인접성 기반보다 더 복잡한 네트워크 구조를 포착할 수 있지만, 그만큼 계산 비용이 더 큽니다. 어떤 방법을 선택할지는 응용 분야와 요구사항에 따라 달라질 수 있습니다.

---

경로 기반 접근법에서의 인접행렬 사용

경로 기반 접근법에서도 인접행렬을 사용합니다. 다만 거리 k에 따른 인접행렬을 만든다는 점이 다릅니다.

동일한 친구 관계 예시로 설명하겠습니다:
철수(1) - 영희(2) - 민수(3) - 지영(4)

1. 거리별 인접행렬 생성:

A¹ (1단계 거리):

A¹ = [
    [0, 1, 0, 0],  # 철수의 직접 친구: 영희
    [1, 0, 1, 0],  # 영희의 직접 친구: 철수, 민수
    [0, 1, 0, 1],  # 민수의 직접 친구: 영희, 지영
    [0, 0, 1, 0]   # 지영의 직접 친구: 민수
]

A² (2단계 거리):

A² = [
    [0, 0, 1, 0],  # 철수의 2단계 친구: 민수
    [0, 0, 0, 1],  # 영희의 2단계 친구: 지영
    [1, 0, 0, 0],  # 민수의 2단계 친구: 철수
    [0, 1, 0, 0]   # 지영의 2단계 친구: 영희
]

A³ (3단계 거리):

A³ = [
    [0, 0, 0, 1],  # 철수의 3단계 친구: 지영
    [0, 0, 0, 0],  # 영희의 3단계 친구: 없음
    [0, 0, 0, 0],  # 민수의 3단계 친구: 없음
    [1, 0, 0, 0]   # 지영의 3단계 친구: 철수
]

2. 임베딩 학습 과정:
   각 학생을 2차원 공간에 표현하되, 거리를 고려합니다:

z_철수 = [0.8, 0.2]
z_영희 = [0.7, 0.3]
z_민수 = [0.5, 0.5]
z_지영 = [0.3, 0.7]

3. 손실 함수 계산 예시:
   철수-민수 관계(k=2)에 대해:

L_{철수,민수} = ||z_철수^T z_민수 - A²_{1,3}||^2
               = ||(0.8×0.5 + 0.2×0.5) - 1||^2
               = ||0.5 - 1||^2
               = 0.25

5. 특징:

• k=1: 직접 연결된 친구들 (실선)

  • 철수-영희
  • 영희-민수
  • 민수-지영

• k=2: 친구의 친구 (점선)

  • 철수-민수
  • 영희-지영

• k=3: 친구의 친구의 친구

  • 철수-지영

6. 장점:

• 다양한 거리의 관계 포착 가능
• 네트워크의 전역적 구조 반영
• 간접적 관계도 고려

7. 한계:

• 계산 복잡도 증가
• k값 선택의 어려움
• 메모리 사용량 증가

이처럼 경로 기반 접근법은 단순히 직접 연결된 관계뿐만 아니라, k단계 떨어진 관계까지 고려하여 더 풍부한 네트워크 구조를 임베딩에 반영할 수 있습니다.