그래프의 정점을 어떻게 백터로 표현할까?

1. 기본 개념 설명
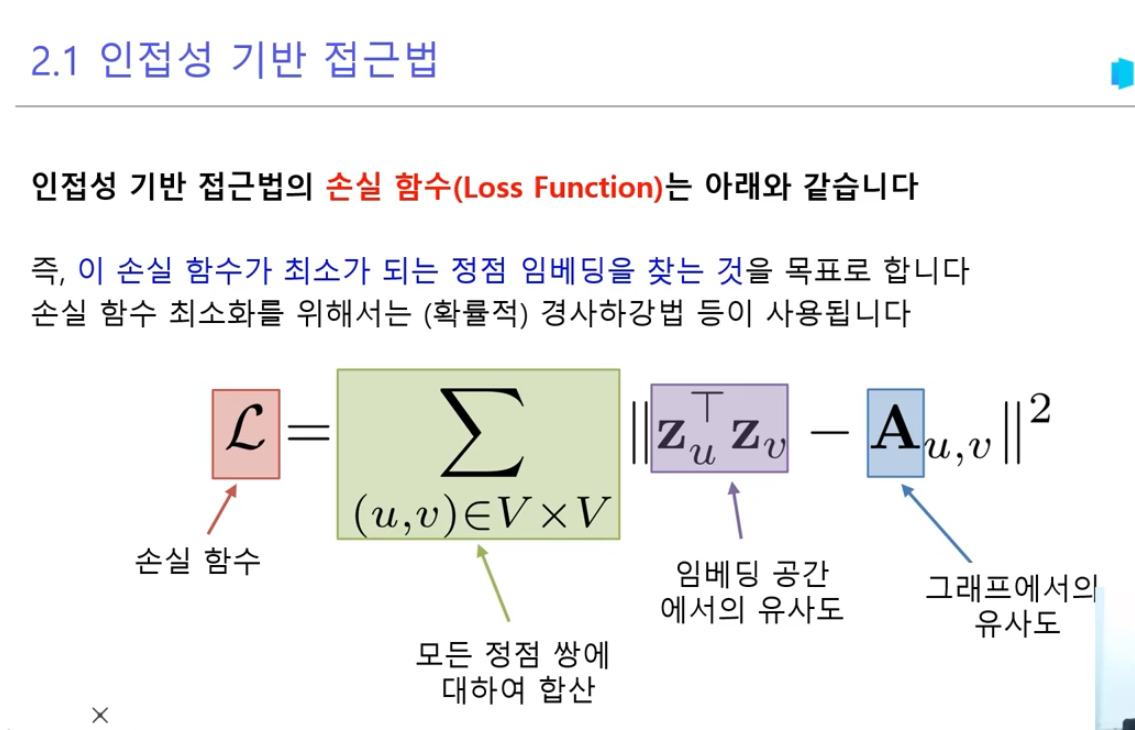
   손실함수 L = Σ ||z_u^T z_v - A_u,v||²는 다음을 의미합니다:

• z_u, z_v: 정점 u와 v의 임베딩 벡터
• A_u,v: 실제 그래프에서 정점 u와 v 사이의 연결 관계
• ||...||²: 유클리드 거리의 제곱

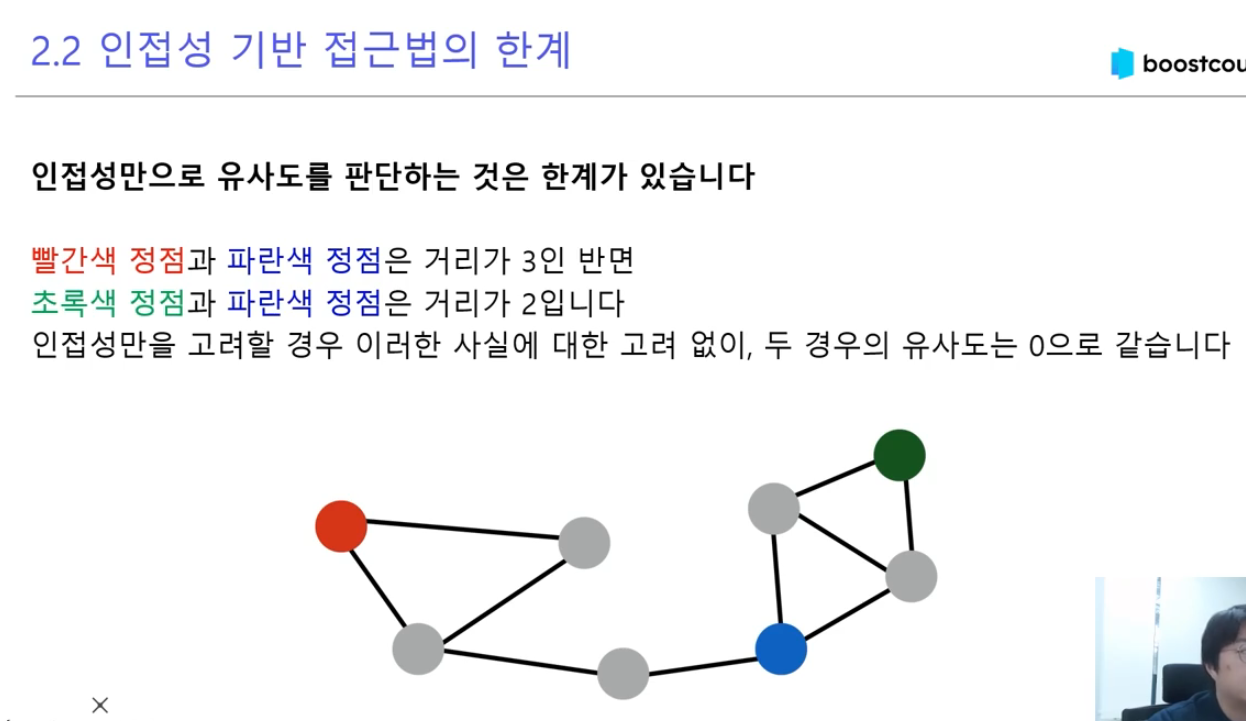
2. 실제 예시를 통한 설명
   작은 소셜 네트워크를 예로 들어보겠습니다:

사용자 3명(A, B, C)이 있는 네트워크에서:

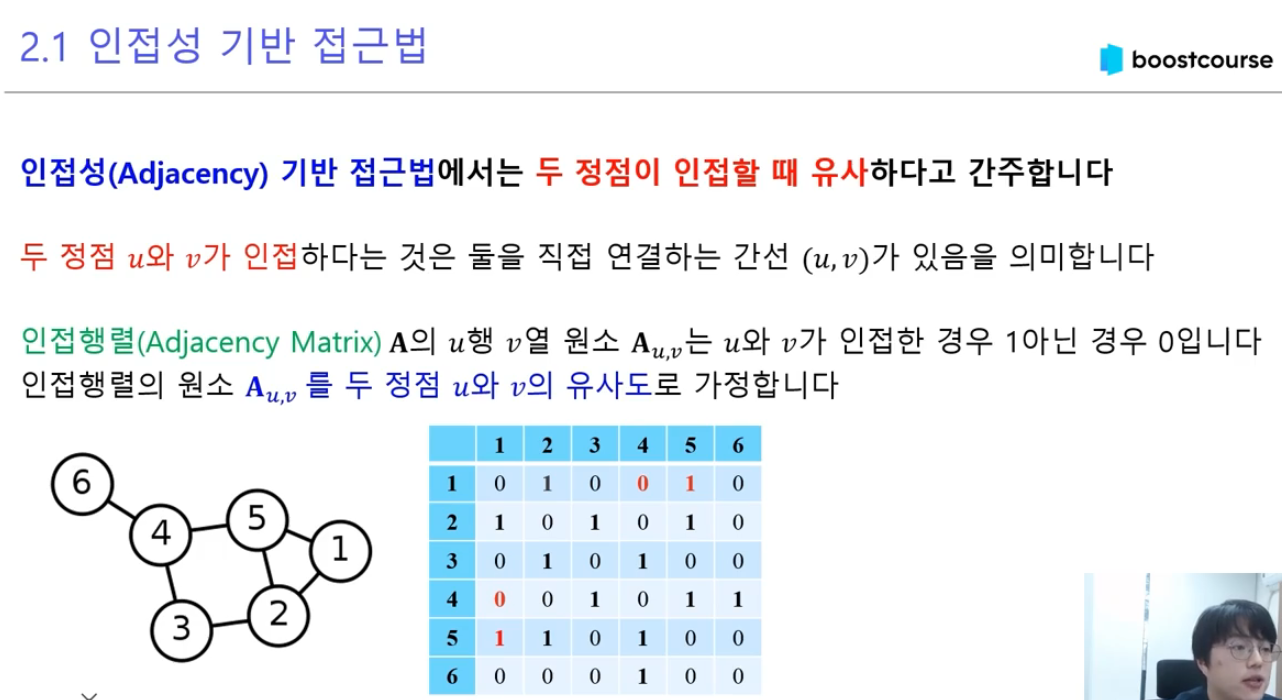
인접 행렬 A = 
    A  B  C
A   1  1  0
B   1  1  1
C   0  1  1

(1: 연결됨, 0: 연결안됨)

3. 임베딩 벡터 초기화 (2차원 예시)

z_A = [0.5, 0.3]
z_B = [0.4, 0.6]
z_C = [0.2, 0.7]

4. 손실함수 계산 과정

A. A-B 관계에 대한 손실:

• 실제 관계(A_AB) = 1
• 예측 관계(z_A^T z_B) = 0.5×0.4 + 0.3×0.6 = 0.38
• 손실 = (0.38 - 1)² = 0.384

B. A-C 관계에 대한 손실:

• 실제 관계(A_AC) = 0
• 예측 관계(z_A^T z_C) = 0.5×0.2 + 0.3×0.7 = 0.31
• 손실 = (0.31 - 0)² = 0.096

C. B-C 관계에 대한 손실:

• 실제 관계(A_BC) = 1
• 예측 관계(z_B^T z_C) = 0.4×0.2 + 0.6×0.7 = 0.5
• 손실 = (0.5 - 1)² = 0.25

총 손실 = 0.384 + 0.096 + 0.25 = 0.73

5. 최적화 목표
   이 손실값을 최소화하는 방향으로 임베딩 벡터들을 조정해야 합니다.

6. 최적화 과정

• 경사하강법을 사용하여 각 임베딩 벡터를 조정
• 예를 들어, z_A를 [0.6, 0.4]로 조정하면:
  • A-B 손실이 감소: (0.6×0.4 + 0.4×0.6 = 0.48) → (0.48-1)² = 0.27
  • 전체적인 손실이 감소하는 방향으로 계속 조정

8. 실제 적용 시 고려사항

• 차원의 수: 보통 16~256차원 사용
• 학습률: 너무 크면 발산, 너무 작으면 수렴 느림
• 정규화: 과적합 방지를 위해 필요
• 네거티브 샘플링: 계산 효율성을 위해 사용

이러한 과정을 통해:
1. 실제 네트워크 구조를 잘 반영하는 임베딩을 학습
2. 노드 간 관계를 벡터 공간에서 효과적으로 표현
3. 새로운 연결 예측이나 노드 분류 등의 작업에 활용 가능

인접성 기반 접근법의 손실함수가 실제로 작동하는 방식입니다.