



상호 배반적이란 두 상품이 동시에 발생할 수 없는 관계
- 올바른 예시:
- 햇반 → 김치 (가능)
- 맥주 → 기저귀 (가능)
- 이들은 서로 다른 카테고리의 상품이며, 독립적으로 구매 가능하기 때문입니다.
- 잘못된 예시:
- 햇반 → 햇반 프리미엄
- 콜라 1.5L → 콜라 2L
- 같은 종류의 상품이라 대체재 관계입니다
- 한 고객이 동시에 구매할 가능성이 낮습니다
- 실질적인 연관성 발견이 어렵습니다
즉, 연관 규칙의 조건절(IF)과 결과절(THEN)에 들어가는 상품들은 서로 겹치지 않고 독립적인 관계여야 의미 있는 분석이 가능합니다.
이는 추천 시스템의 품질을 높이기 위한 중요한 조건입니다. 서로 대체 가능한 상품들을 추천하는 것보다, 실제로 함께 구매될 가능성이 있는 상품들을 추천하는 것이 더 유용하기 때문입니다.




Lift와 Leverage의 주요 차이점
- 계산 공식의 차이:
- Leverage = P(A,B) - P(A) × P(B) (차이/뺄셈 사용)
- Lift = P(A,B) / (P(A) × P(B)) (비율/나눗셈 사용)
- 해석 방법의 차이:
Leverage:
- 값의 범위: -1 ~ +1 사이
- 0: 두 품목이 독립적
- 양수: 양의 상관관계
- 음수: 음의 상관관계
- 절대값이 클수록 연관성이 강함
Lift:
- 값의 범위: 0 ~ ∞ (무한대)
- 1: 두 품목이 독립적
- 1보다 크면: 양의 상관관계
- 1보다 작으면: 음의 상관관계
- 1에서 멀어질수록 연관성이 강함
- 실제 예시로 비교:
앞의 예제 데이터 사용 (100명 중)
- 과자(A): 40명
- 음료(B): 50명
- 동시구매(A,B): 30명
Leverage 계산:
= 0.3 - (0.4 × 0.5)
= 0.3 - 0.2
= 0.1
Lift 계산:
= 0.3 / (0.4 × 0.5)
= 0.3 / 0.2
= 1.5
- 주요 특징:
- Leverage는 절대적 차이를 보여줌
- Lift는 상대적 비율을 보여줌
- Lift는 희귀한 항목들 간의 관계를 더 잘 포착할 수 있음
- Leverage는 빈도가 높은 항목들의 관계를 더 잘 포착
따라서 분석 목적에 따라 적절한 지표를 선택해야 합니다:
- 전반적인 연관성 파악: Lift
- 실제 발생 빈도의 차이 분석: Leverage
실제 마트 쇼핑 예시
1. 희귀 항목 vs 빈도 높은 항목 비교
총 1000명의 고객 데이터로 예시를 들어보겠습니다.
케이스 1: 희귀 항목 (고가의 와인과 치즈)
- 와인 구매(A): 30명 (P(A) = 0.03)
- 고급치즈 구매(B): 40명 (P(B) = 0.04)
- 동시구매(A,B): 10명 (P(A,B) = 0.01)
Lift 계산:
= 0.01 / (0.03 × 0.04)
= 0.01 / 0.0012
= 8.33
Leverage 계산:
= 0.01 - (0.03 × 0.04)
= 0.01 - 0.0012
= 0.0088
케이스 2: 빈도 높은 항목 (우유와 빵)
- 우유 구매(A): 400명 (P(A) = 0.4)
- 빵 구매(B): 500명 (P(B) = 0.5)
- 동시구매(A,B): 300명 (P(A,B) = 0.3)
Lift 계산:
= 0.3 / (0.4 × 0.5)
= 0.3 / 0.2
= 1.5
Leverage 계산:
= 0.3 - (0.4 × 0.5)
= 0.3 - 0.2
= 0.1
해석:
1. 희귀 항목 (와인-치즈):
- Lift = 8.33 → 매우 강한 연관성 보여줌
- Leverage = 0.0088 → 약한 연관성처럼 보임
2. 빈도 높은 항목 (우유-빵):
- Lift = 1.5 → 보통 수준의 연관성
- Leverage = 0.1 → 상당한 연관성으로 보임
이를 통해:
1. Lift는 실제 발생 빈도가 낮더라도(와인-치즈) 두 항목 간의 상대적 연관성이 높으면 큰 값을 보여줍니다.
2. Leverage는 실제 동시 구매 빈도가 높은 항목(우유-빵)에서 더 의미 있는 수치를 보여줍니다.
실무 적용:
1. 고가 상품이나 계절 상품같이 구매 빈도가 낮은 항목들의 연관성 분석 → Lift 사용
예: 제주도 여행 상품과 렌터카 상품
2. 일상적으로 자주 구매되는 품목들의 실질적 연관성 분석 → Leverage 사용
예: 장바구니 분석에서 생필품들 간의 관계
따라서:
- 전반적인 연관성(특히 희귀 항목): Lift가 더 적합
- 실제 구매 빈도를 고려한 분석: Leverage가 더 적합
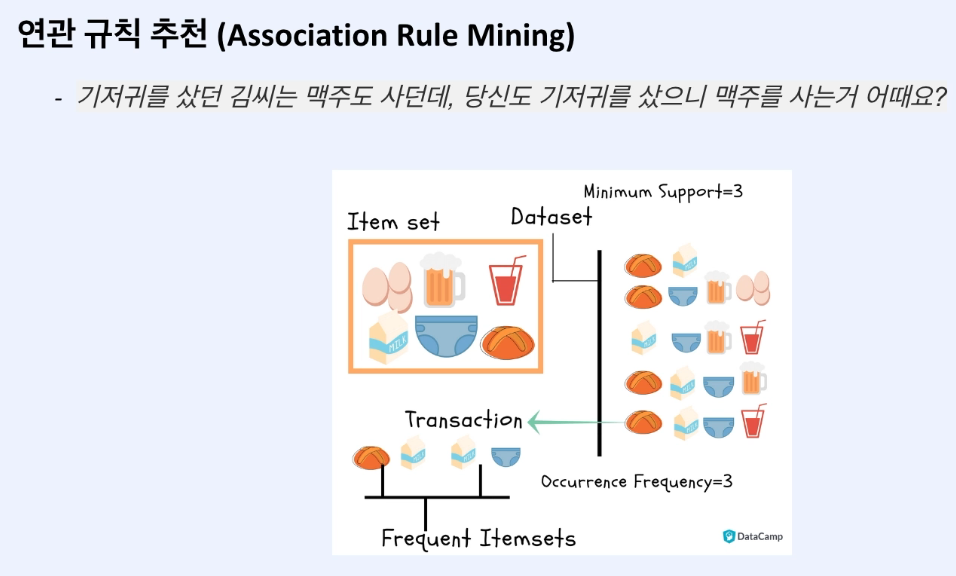
예시: 작은 슈퍼마켓의 거래 데이터를 분석하는 상황을 가정
거래 데이터 (총 5건의 거래):
1번: {우유, 빵, 버터}
2번: {우유, 빵}
3번: {우유, 빵, 계란}
4번: {빵, 버터}
5번: {우유, 빵, 버터, 계란}
최소 지지도(minimum support)를 40%(0.4)로 설정했다고 가정하겠습니다.
1단계: 1-항목집합 찾기
각 항목의 지지도 계산:
- 우유: 4/5 = 0.8 (80%)
- 빵: 5/5 = 1.0 (100%)
- 버터: 3/5 = 0.6 (60%)
- 계란: 2/5 = 0.4 (40%)
모든 항목이 최소 지지도 0.4를 만족하므로 모두 빈발 1-항목집합이 됩니다.
2단계: 2-항목집합 생성 및 검사
가능한 2-항목집합의 지지도 계산:
- {우유, 빵}: 4/5 = 0.8 (80%)
- {우유, 버터}: 2/5 = 0.4 (40%)
- {우유, 계란}: 2/5 = 0.4 (40%)
- {빵, 버터}: 3/5 = 0.6 (60%)
- {빵, 계란}: 2/5 = 0.4 (40%)
- {버터, 계란}: 1/5 = 0.2 (20%) → 제거됨
3단계: 3-항목집합 생성 및 검사
남은 항목들로부터 3-항목집합 생성:
- {우유, 빵, 버터}: 2/5 = 0.4 (40%)
- {우유, 빵, 계란}: 2/5 = 0.4 (40%)
- {빵, 버터, 계란}: 1/5 = 0.2 (20%) → 제거됨
4단계: 4-항목집합 생성 및 검사
- {우유, 빵, 버터, 계란}: 1/5 = 0.2 (20%) → 제거됨
최종적으로 발견된 빈발 항목집합들:
- 1-항목: {우유}, {빵}, {버터}, {계란}
- 2-항목: {우유,빵}, {우유,버터}, {우유,계란}, {빵,버터}, {빵,계란}
- 3-항목: {우유,빵,버터}, {우유,빵,계란}
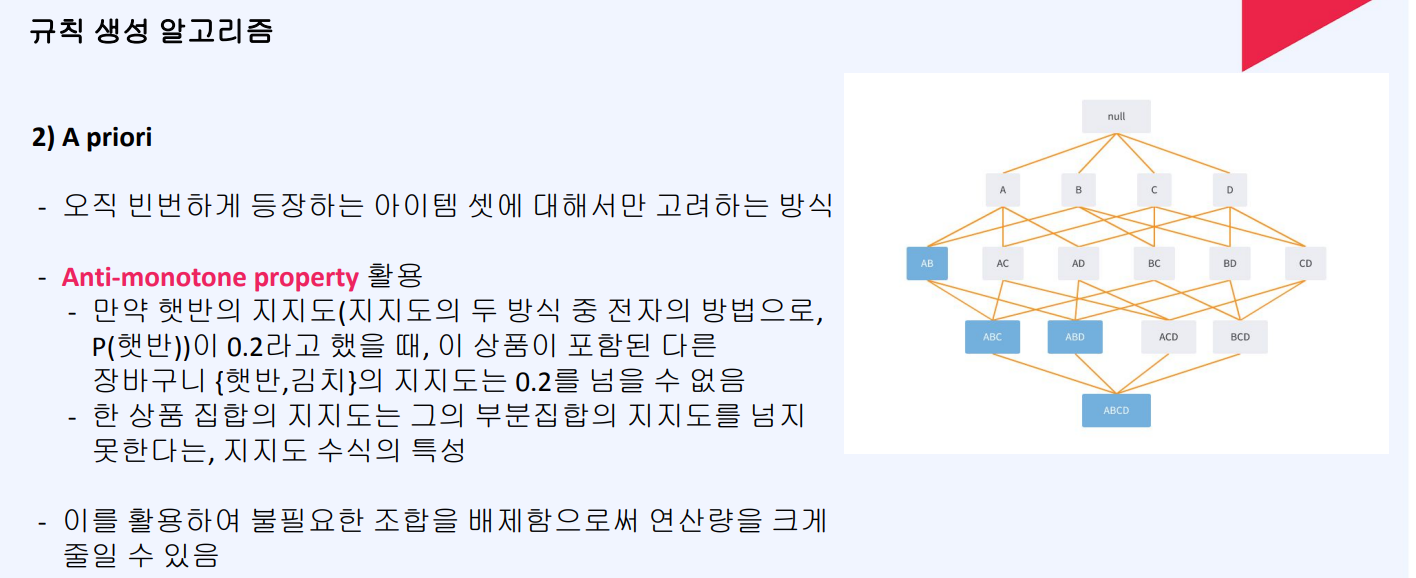
이 예시에서 Anti-monotone property가 적용된 것을 볼 수 있습니다:
- {버터,계란}이 빈발하지 않으므로, 이를 포함하는 모든 상위 항목집합({빵,버터,계란}, {우유,버터,계란} 등)은 자동으로 제외되었습니다.
- 이를 통해 모든 가능한 조합을 검사하지 않고도 효율적으로 빈발 항목집합을 찾을 수 있었습니다.
