이진 탐색 트리

이진 탐색 트리(BST)란 이진트리 기반 탐색을 위한 자료구조이다.

특징

이진 탐색 트리에는 다음과 같은 속성이 있다.

• 모두 유일한(중복되지 않는) 키 값을 가진다.
• 왼쪽과 오른쪽의 서브트리도 이진트리여야 한다.
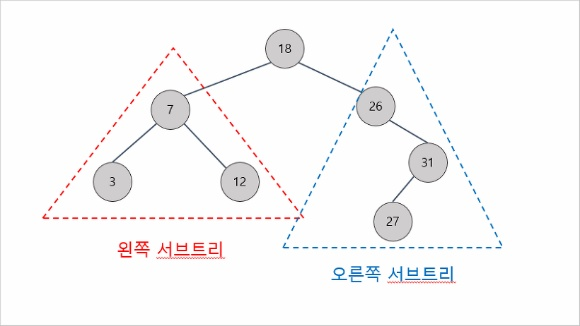
• 노드의 왼쪽 서브트리는 루트의 키보다 작은 값을 가진다.
• 노드의 오른쪽 서브트리는 루트의 키보다 큰 값을 가진다.
  

이진 탐색 트리에서 root 노드를 기준으로 왼쪽 서브트리의 가장 왼쪽 값이 트리에서 가장 작은 값, 오른쪽 서브트리의 가장 오른쪽 값이 트리에서 가장 큰 값이 된다.
또한 왼쪽 서브트리의 가장 오른쪽 값이 root 값 보다 작은 값들 중 가장 큰 값이 되며, 오른쪽 서브트리의 가장 왼쪽 값이 root 값 보다 큰 값들 중 가장 작은 값이 된다.

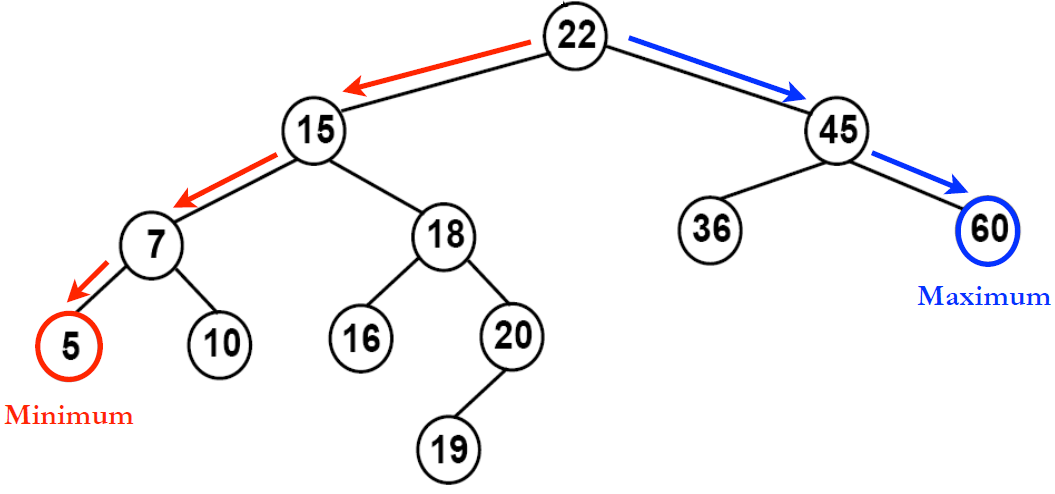
위 트리 기준
왼쪽 서브트리에서 가장 작은 값 : 5 <- 트리에서 가장 작은 값
왼쪽 서브트리에서 가장 큰 값 : 20 <- 루트 다음으로 작은 값
오른쪽 서브트리에서 가장 작은 값 : 36 <- 루트 다음으로 큰 값
오른쪽 서브트리에서 가장 큰 값 : 60 <- 트리에서 가장 큰 값

연산

밑에 작성되는 예시는 다음 사진을 기준으로 작성할 것이다.

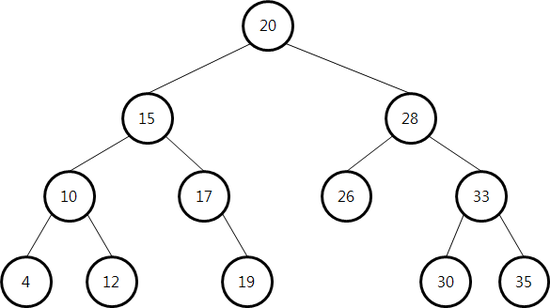
탐색

이진탐색트리의 탐색은 다음과 같다.

1. 찾고자 하는 값과 root 값을 비교한다.
2. 찾고자 하는 값이 root 값보다 작을 경우 왼쪽 서브트리에서, 클 경우 오른쪽 서브트리에서 탐색한다.
3. 찾고자 하는 값을 찾을 때까지 반복한다.
4. 만일 찾고자 하는 값이 없다면 null을 반환한다.

위 트리에서 26이란 값을 찾는다면 다음과 같은 순서로 진행된다.

1. 찾고자 하는 26과 root 값인 20을 비교 -> 찾고자 하는 값이 더 크므로 root를 28로 이동
2. 찾고자 하는 26과 root 값인 28을 비교 -> 찾고자 하는 값이 더 작으므로 root를 26으로 이동
3. 찾고자 하는 26과 root 값인 26을 비교 -> 찾고자 하는 값을 찾았으므로 탐색 종료(만일 없다면 Null 반환)

삽입

이진 탐색 트리에서 데이터를 삽입하기 이전에 먼저 탐색연산을 먼저 진행한다.
삽입하기 이전에 삽입하고자 하는 데이터가 존재하는지를 탐색한 뒤, 데이터가 없다면 해당 위치에 데이터를 삽입한다.

위 트리에서 16이란 값을 삽입하고자 하면 다음과 같은 순서로 진행된다.

1. 찾고자 하는 16과 root 값인 20과 비교 -> 찾고자 하는 값이 더 작으므로 root를 15로 이동
2. 찾고자 하는 16과 root 값인 15를 비교 -> 찾고자 하는 값이 더 크므로 root를 17로 이동
3. 찾고자 하는 16과 root 값인 17을 비교 -> 찾고자 하는 값이 더 작지만 왼쪽 값이 없으므로 Null 반환
4. Null이 반환 됐으므로 그 자리에 16값 삽입

삭제

이진 탐색 트리에서 데이터를 삭제할 때도 삽입과 마찬가지로 탐색 연산을 먼저 진행해야 한다.
삭제하기 이전에 삭제하고자 하는 데이터가 존재하는지를 탐색한 뒤, 데이터가 있다면 해당 데이터를 삭제한다.

위 트리에서 30이란 값을 삭제하고자 하면 다음과 같은 순서로 진행된다.

1. 찾고자 하는 30과 root 값인 20을 비교 -> 찾고자 하는 값이 더 크므로 root을 28로 이동
2. 찾고자 하는 30과 root 값인 28을 비교 -> 찾고자 하는 값이 더 크므로 root을 33으로 이동
3. 찾고자 하는 30과 root 값인 33을 비교 -> 찾고자 하는 값이 더 작으므로 root를 30으로 이동
4. 찾고자 하는 30과 root 값인 30을 비교 -> 찾고자 하는 값을 찾았으므로 해당 값을 삭제

Reference

• [자료구조] 이진탐색트리 (Binary Search Tree)
• [자료구조] 이진 탐색 트리 (BST, Binary Search Tree)