
이진 트리(Binary Tree)
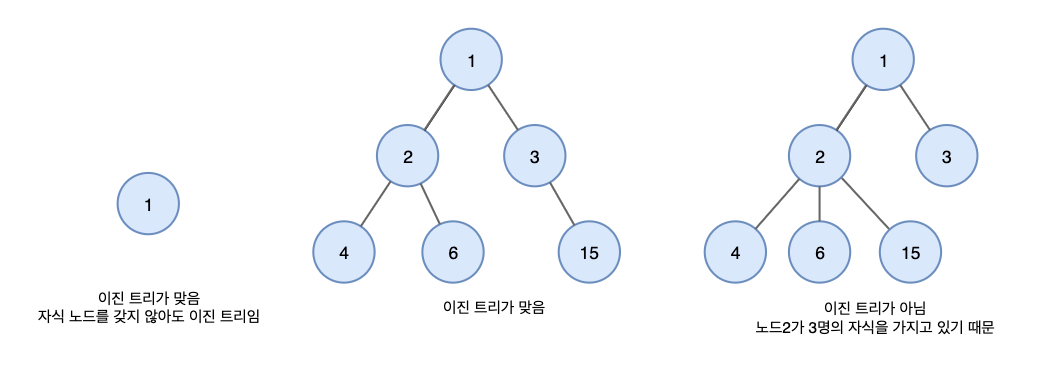
이진트리는 자식 노드가 최대 두 개인 노드들로 구성된 트리이다.
컴퓨터 응용에서 가장 많이 활용되는 트리 구조로, 모든 노드가 두 개의 서브트리를 가지고 있다.
모든 노드들이 2개 이하의 자식노드를 갖기 때문에 왼쪽, 오른쪽 개념부여가 가능하다.
이진 트리의 종류
- 전 이진 트리(Full Binary Tree)
- 완전 이진 트리(Complete Binary Tree)
- 포화 이진 트리(Perfect Binary Tree)
- 균형 이진 트리 (Balanced Binary Tree)
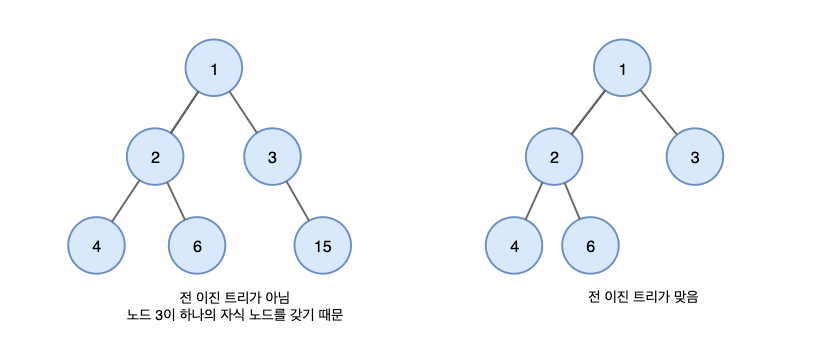
전 이진 트리(Full Binary Tree)
전 이진 트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
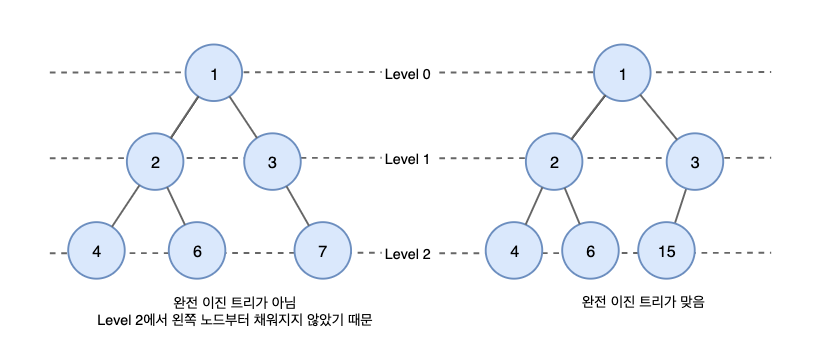
완전 이진 트리(Complete Binary Tree)
완전 이진 트리는 부모, 왼쪽 자식, 오른쪽 자식 순으로 채워지는 트리를 말하며, 마지막 레벨을 제외하고 모든 노드가 가득 차 있어야 함
마지막 레벨의 노드도 왼쪽으로 몰려 있어야 하며, 중간에 빈 곳이 없어야 한다.
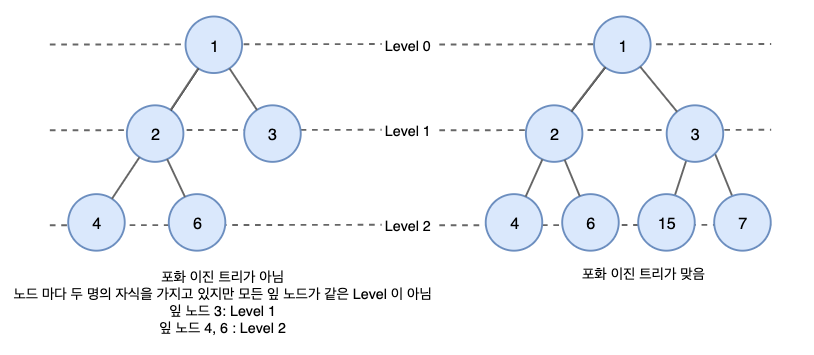
포화 이진 트리(Perfect Binary Tree)
포화 이진 트리는 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 이진 트리
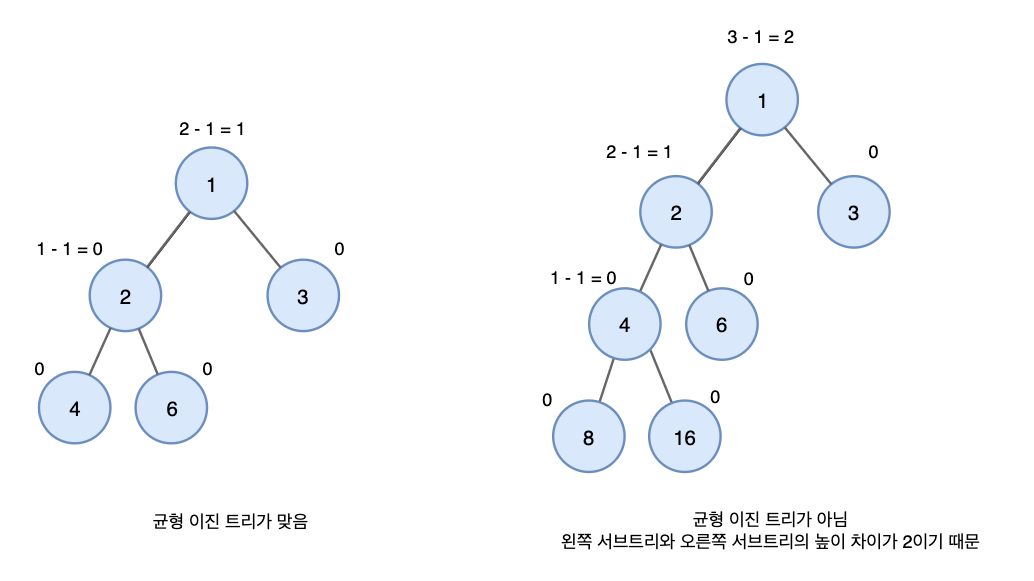
균형 이진 트리 (Balanced Binary Tree)
균형 이진 트리는 왼쪽과 오른쪽 트리의 높이 차이가 모두 1만큼 나는 트리입니다. 예를 들어 AVL 및 Red-Black 트리는 균형 이진 트리
이진트리 속성
-
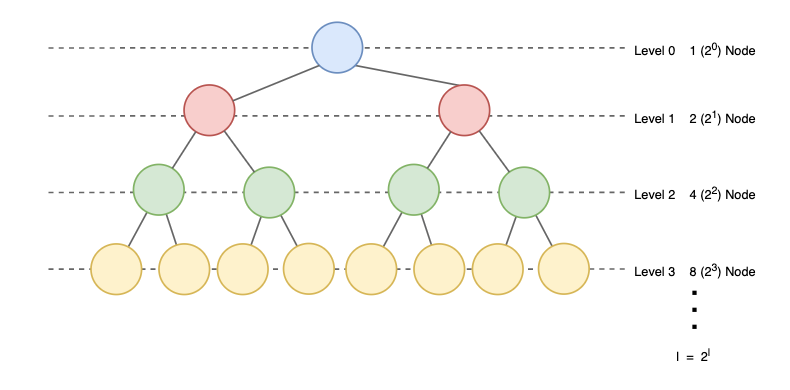
이진 트리의 레벨 l에서의 노드의 최대 수는 2l 이다.
-
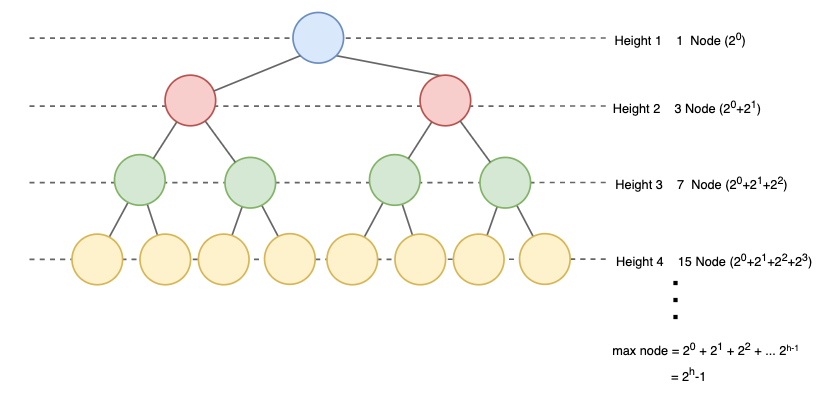
높이가 h이고 하나의 노드를 가진 트리의 높이가 1이라면 최대 노드 수는 2^h^ -1이고 높이가 0이라면 2 h+1 -1이다.
-
단말 노드 높이가 1이라면 최소 높이는 log 2 (N+1)이고, 단말 노드의 높이가 0이라면 log 2 (N+1)-1이다.
2 h -1 = n
2 h = n+1
log 2 (2 h ) = log 2 (N+1)
h = log 2 (N+1) -
전 이진트리에서 단말 노드 수는 항상 자식이 두 개인 노드보다 하나 더 많다.
L = 단말 노드 수
T = 두 명의 자식을 가진 내부 노드 수
L = T + 1
이진트리 표현
이진 트리는 배열로도 표현할 수 있고 연결리스트로 표현할 수도 있다.
배열의 경우 필자가 정리한 힙에서 특징 부분에서 설명하였다.
연결리스트의 경우 Left와 Right를 통해서 자식 노드에 접근할 수 있다.
연결리스트는 배열보다는 느리지만, 삽입 삭제가 쉽고 노드 수에 제한이 없다.
이진 트리 순회
트리의 모든 노드를 방문하는 과정을 트리 순회(Tree Traversal)이라고 한다.
노드를 하나도 빠뜨리지 않고 정확히 한 번만 중복없이 반복하는 작업을 말한다.
트리를 순회하는 방법은 다음과 같이 존재한다.
- 전위 순회(Preorder): VLR
- 중위 순회(Inorder): LVR
- 후위 순회(Postorder): LRV
- 레벨 순회(level-order)
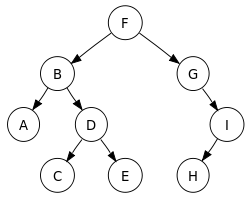
전위 순회(Preorder)
전위 순회는 깊이 우선 순회(Depth-Frist Traversal)라고도 불린다.
전위 순회는 다음과 같은 방법으로 진행된다.
- 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회한다.
방문 순서 : F -> B -> A -> D -> C -> E -> G -> I -> H
중위 순회(Inorder)
중위 순회는 대칭 순회(symmetric)라고도 한다.
- 왼쪽 서브 트리를 중위 순회한다.
- 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
방문 순서 : A -> B -> C -> D -> E -> F -> G -> H -> I
후위 순회(Postorder)
- 왼쪽 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- 노드를 방문한다.
방문 순서 : A -> C -> E -> D -> B -> H -> I -> G -> F
레벨 순회(level-order)
레벨 순서 순회는 모든 노드를 낮은 레벨부터 차례대로 순회한다.
레벨 순서 순회는 너비 우선 순회(breadth-first traversal)라고도 한다.
방문 순서 : F -> B -> G -> A -> D -> I -> C -> E -> H
