시퀀스 데이터
시퀀스 데이터: 순차적으로 들어오는 데이터. 소리, 문자열, 주식 가격 등.
시계열(time-series) 데이터는 시간 순서에 따라 나열된 데이터로 시퀀스 데이터에 속한다.
시퀀스 데이터는 독립동등분포(i.i.d.)가정을 위배하기 쉽기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀐다.
e.g.) 문자열의 경우: '개가 사람을 물었다 <-> 사람이 개를 물었다' 같이 순서를 바꾸면 의미, 데이터의 빈도 등이 바뀌게 됨.
시퀀스 데이터 다루기
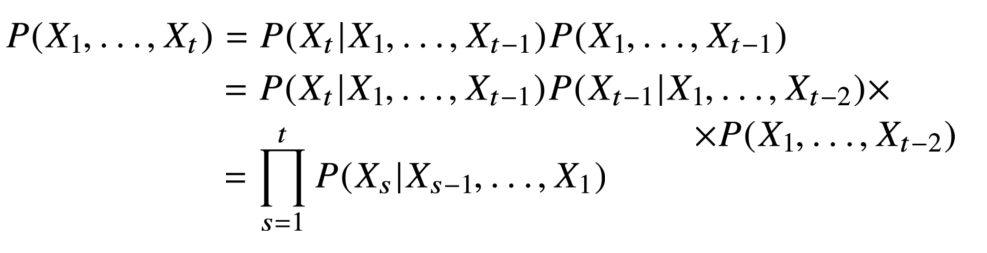
조건부확률을 이용해 이전 시퀀스의 정보를 바탕으로 앞으로 발생할 데이터의 확률분포를 예측할 수 있다.
하지만 과거의 모든 정보가 필요한 것은 아니다.
AR(τ)(Autogressive Model) 자기회귀모델
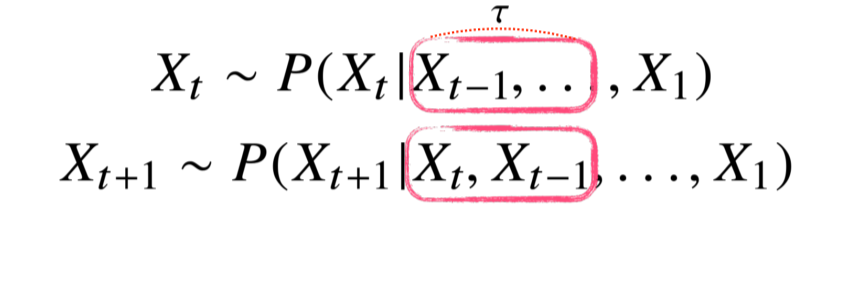
- 고정된 길이τ만큼 시퀀스를 사용하는 경우
τ를 결정하는 것도 사전지식이 필요할 때가 있다는 것이 문제.
잠재 AR 모델
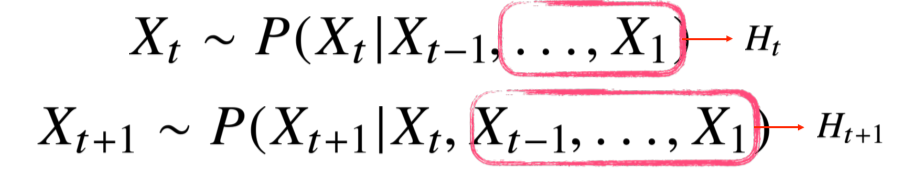
-
바로 이전 정보를 제외한 나머지 정보들을 Ht라는 잠재변수로 인코딩해서 활용
-
고정된 길이의 데이터, 과거의 모든 데이터를 갖고 모델링 할 수 있는 것이 장점.
하지만 과거의 정보들을 잠재변수로 어떻게 encoding할지가 문제.
RNN(Recurrent Neural Network)
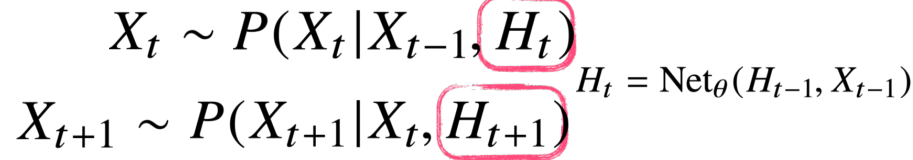
- Ht를 neural network를 통해 과거 바로 이전의 정보와 이전 잠재변수의 모형을 갖고 예측
RNN(Recurrent Neural Network)
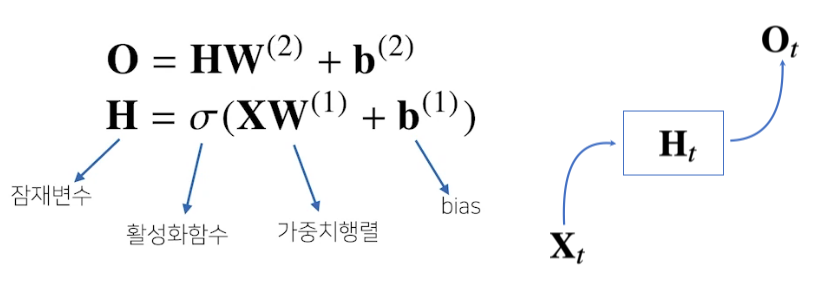
- : 1, 2번째 layer의 weight. 시퀀스 데이터에 상관없이 불변.
위 모델은 현재의 입력만 다루기 때문에 과거의 정보를 잠재변수에 다룰 수 없다는 단점이 존재.
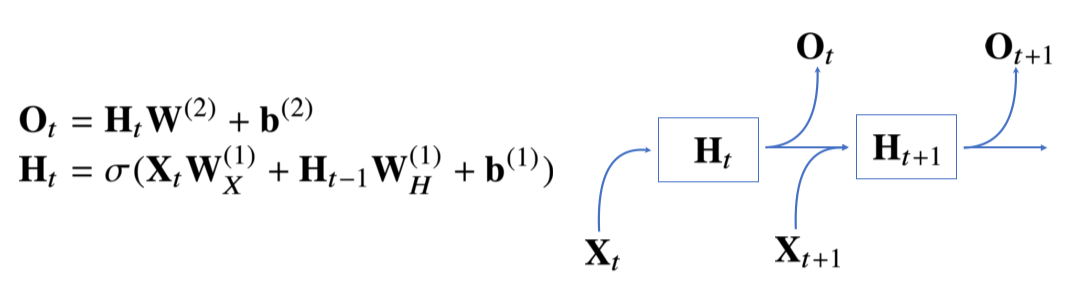
: 이전 잠재벡터로부터 정보를 전달받음
: 현재 입력으로부터 전달받음
: 잠재벡터로부터 출력을 만들어줌
, , 모두 에 따라 변하지 않음!
에 따라 변하는 것은 잠재변수와 입력뿐
BPTT(Backpropagation Through Time)
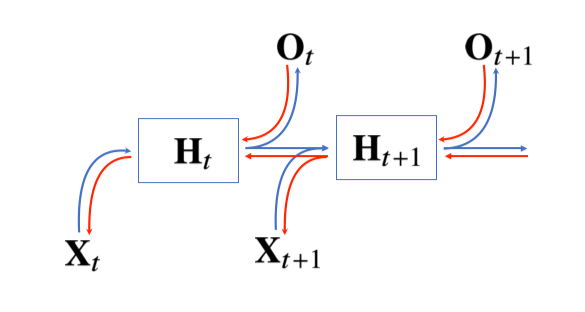
BPTT는 가장 마지막 시점의 gradient가 역으로 RNN을 타고 올라오면서 업데이트됨
에 들어오는 gradient vector는 2개: 에서 들어오는 vector, 에서 들어오는 vector
BPTT를 계산한 수식

- 위 수식은 ~ 까지의 모든 의 미분곱
해당 수식은 시퀀스 길이가 길어질수록 불안정해짐. 이 값이 1보다 크면 미분값이 매우 커지고, 1보다 작으면 한없이 작아지기 때문.
특히 gradient가 작아지면(기울기가 0으로 되면) 정보를 유실할 위험이 있다.
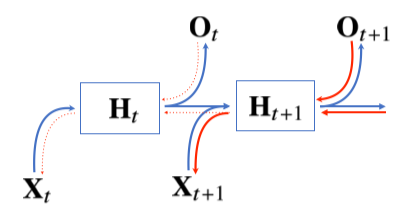
- 이를 개선하기 위해 truncated BPTT를 이용, 길이를 나눠 특정 block에서 끊고 gradient를 나눠서 전달.
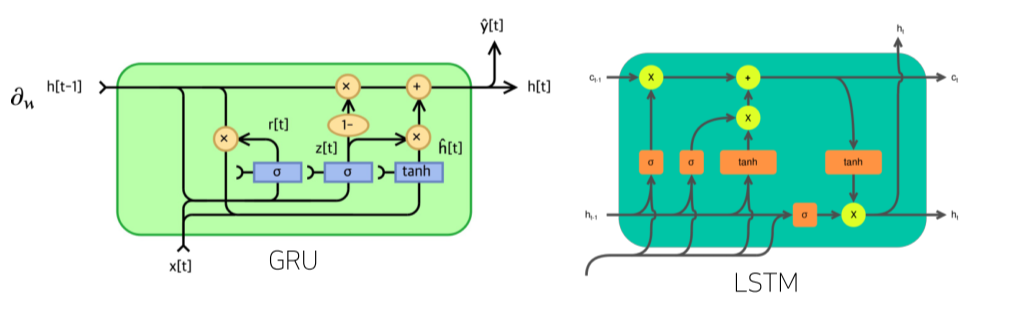
- 요즘엔 길이가 긴 시퀀스를 처리할때 GRU, LSTM 등 다른 모델을 사용함.
GRU, LSTM에 대한 정리는 다음 글에서..