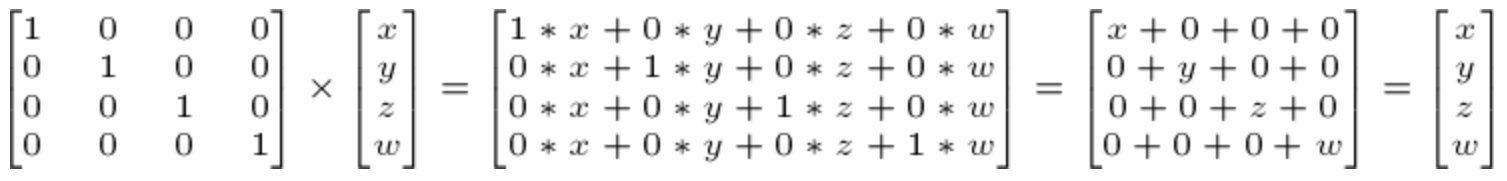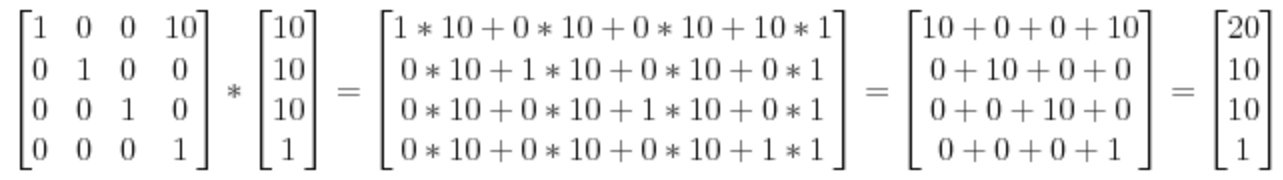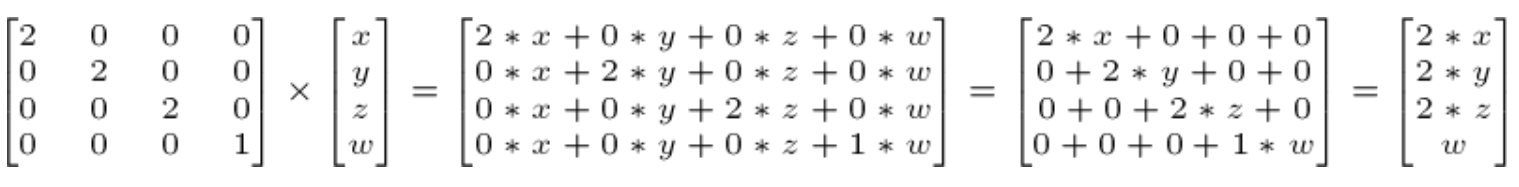OpenGL 개념정리

1. 정점(Vertext)

좌표이며 색상정보를 가지고 있음. 2d는 x, y 3d는 x, y, z로 표시되며 색상은 RGBA(red, green, blue, alpha)로 표시됨.

---

2. 폴리곤(Polygon)

정점을 연결해서 만든 면(ex. 3개를 연결하면 삼각형)

• 2.1. 폴리곤 매쉬(Polygon Mesh)
  폴리곤이 모여있는 집합. 흔히 mesh라 불림.

---

3. 쉐이더(Shader)

정점을 바탕으로 화면을 그려주는 프로그램 코드. 정점 쉐이더(Vertex Shader)와 프레그먼트 쉐이더(Fragment Shader)가 있다.

• 3.1. 정점 쉐이더(Vertex Shader)
  정점의 최종 위치를 계산하는 역할. 정점마다 한 번 씩 실행되며 정점이 모여 점, 선, 면(삼각형)을 이루게 됨.
• 3.2 프레그먼트 쉐이더(Fragment Shader)
  정점 쉐이더로 생성된 점, 선, 면(삼각형)의 최종 색상을 계산. 각 프레그먼트마다 한 번 실행.

---

4. 래스터화(Rasterization)

정점 쉐이더를 통해 변환된 데이터를 프레그먼트 쉐이더에서 처리 할 수 있도록 데이터를 변환해주는 작업.
정점 쉐이더로 만들어진 면(삼각형)은 래스터화를 거쳐 프레그먼트 쉐이더에서 색상이 입혀지게 됨.

---

5. 텍스쳐(Texture)

화면에 그려질 이미지 데이터. 쉐이더를 거쳐 화면에 그려짐.

---

6. 렌더링 파이프라인(Rendering Pipeline)

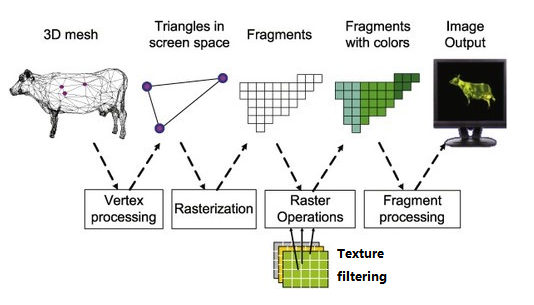
데이터가 정점에서부터 시작되어 면이 되고 색상이 입혀져 화면에 그려지기 까지의 처리과정.

---

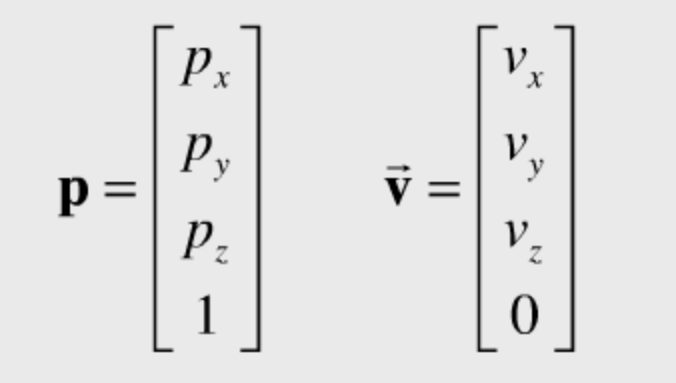
7. 벡터(Vector)

하나의 정점은 하나의 벡터로 표현 될 수 있으며 방향이나 크기를 나타낼 수 있음.

• 방향 > 원점에서 벡터(50, 50, 0)까지의 방향
• 거리 > 원점에서 벡터(50, 50, 0)까지의 거리

OpenGL에서 vec3는 부동소수점(x, y, z)를 의미하고 vec4는 부동소수점(x,y,z,w)를 의미함.
w는 동차좌표로 나타내기 위해 사용.

• 7.1. 동차좌표(Homogeneous Coordinates)
  • 벡터(x, y, z)는 위치를 뜻하기도 하지만 방향을 뜻하기도 함.
  • 위치인지 방향인지 구별하기 위해 생겨난 게 w가 있는 동차좌표임.
  • w=1 이면, (x,y,z,1)는 공간상에서의 위치.
  • w=0 이면, (x,y,z,0)는 방향.
  • 표현 시 w값이 1인 이유는 x, y, z 값이 나중에 w로 나뉘게 되는데 해당 값이 1이어야 값이 변하지 않기 때문.
  • 동차좌표는 벡터(x, y, z)를 4x4 매트릭스와 곱하기 위해 요소를 늘려주는 용도로도 사용함.

---

8. 매트릭스(Matrix)

3차원 이미지를 2차원 평면에 그려내기 위해 사용되는 행렬. OpenGL 은 4x4 정방행렬을 주로 사용함.
오브젝트를 움직이게 하기 위해선 정점(vertex)을 수정하고 버퍼를 재구성 해야함.
이를 위해 사용되는 것이 매트릭스임.
맥트릭스를 벡터와 곱하게 되면 새로운 벡터를 만들 수 있음(곱하는 순서 중요)

• 8.1. 단위행렬(Identity Matrix)

  

  임의의 벡터를 행렬과 곱해도 벡터가 변하지 않는 행렬을 단위행렬이라고 함.
  벡터(x,y,z,w)를 매트릭스와 곱해도 여전히 (x,y,z,w)이므로 위 행렬은 단위행렬임.

  안드로이드에서는 setIdentityM 메서드로 생성할 수 있음.

  float[] matrix = new float[16]; 
  Matrix.setIdentityM(matrix, 0);

• 8.2. 평행이동 행렬(Translation Matrix)
  
  정점을 어느 방향으로 이동 시킬 수 있는 행렬.
  
  위 행렬의 X, Y, Z 값에 값을 입력하면 해당 값 만큼 X, Y, Z 축으로 이동 시킬 수 있다. 위 예시의 경우 정점(10, 10, 10) 을 X 방향으로 10만큼 이동시킨 결과.

  안드로이드에서는 translateM 메서드로 생성할 수 있음.

  float[] matrix = new float[16];
  Matrix.setIdentityM(matrix, 0);
  Matrix.translateM(matrix, 0, 10,0,0); 

• 8.3. 확대/축소 행렬(Scaling Matrix)
  

  벡터값을 확대/축소 시킬 수 있는 행렬.
  위 행렬의 X, Y, Z 값에 값을 입력하면 해당 값 만큼 X, Y, Z 축으로 확대/축소 시킬 수 있다.
  정점(x, y, z)를 두배 확대 시키는 예

  안드로이드에서는 scaleM메서드로 생성할 수 있음.

  float[] matrix = new float[16];
  Matrix.setIdentityM(matrix, 0);
  Matrix.scaleM(matrix, 0, 10,0,0); 

• 8.4. 회전 매트릭스(Rotation Matrix)
  

  벡터 값을 삼각함수를 통해 한 축을 기준으로 회전시킬 수 있는 행렬.
  한 축을 기준으로 어느 각(쎄타)만큼 이동시킬 때 아래 와 같은 매트릭스가 사용됨.
  오브젝트를 x, y, z 축 으로 모두 회전 시킬 때, 위에서 구한 행렬 값을 순서대로 곱하면 됨(일명 오일러각(Euler Angles)
  순서 매우 중요. x, y, z 축은 서로 종속적이기 때문에 한 축이 회전 할 때 다른 축에 영향을 미침.
  따라서 곱하는 순서에 따라 최종 방위가 달라지므로 순서를 지켜야 한다.
  일반적으로 ZXY(Roll-Pitch-Yaw) 또는 XYZ 회전이 주로 사용.

  안드로이드에서는 setRotateM메서드로 생성할 수 있음.

  Matrix.setRotateM(float[] rm, int rmOffset, float a, float x, float y, float z)
  // rm : 매트릭스
  // rmOffset : 매트릭스 배열의 시작점, float형 16개짜리 배열을 사용한다면 당연히 0이 된다.
  // a : 회전하고자 하는 각도
  // x : x축 회전 벡터
  // y : y축 회전 벡터
  // z : z축 회전 벡터

---

9. MVP 매트릭스(MVP Matrix)

3D공간에서 오브젝트를 표현하기 위한 매트릭스. Model, View, Projection의 약자.

• 9.1. Model
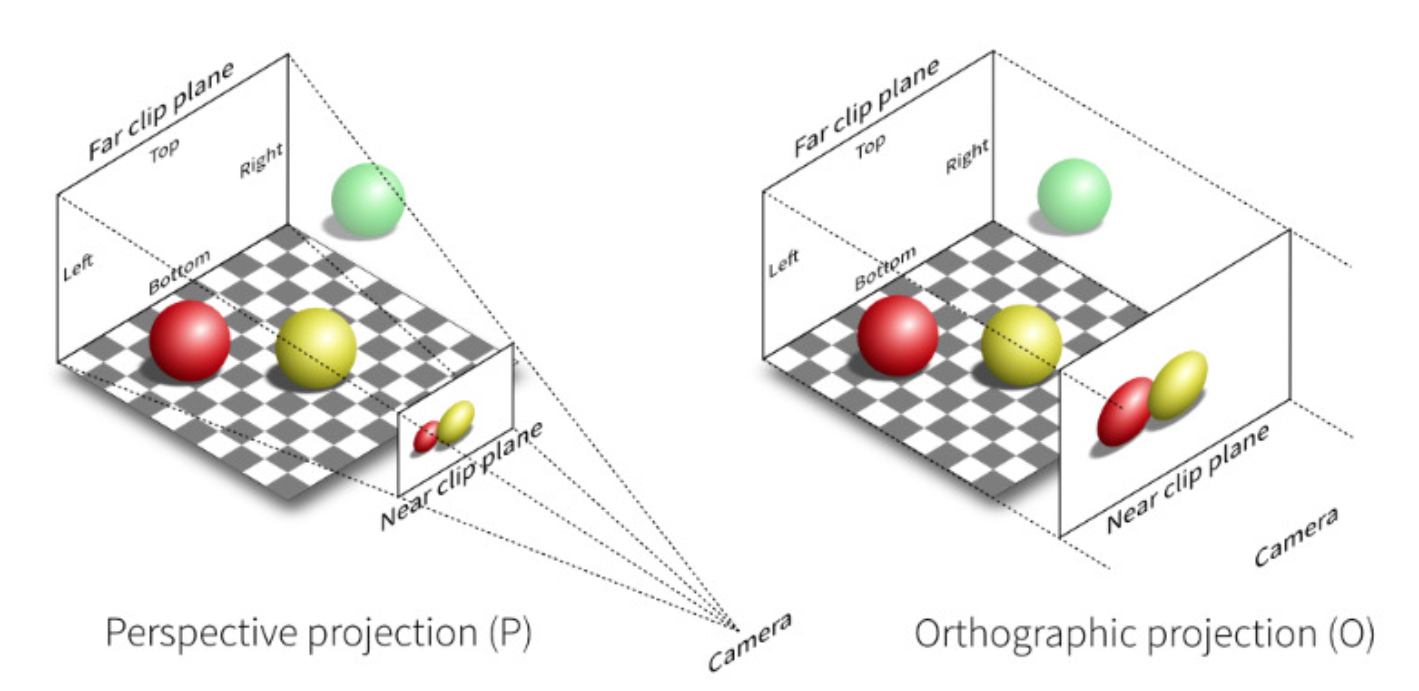
  그리고자 하는 대상인 물체. 위 사진상의 구체.
• 9.2. View
  Model을 바라보는 시점(= 카메라)
• 9.3. Projection
  카메라가 모델을 볼 수 있는 화각. 카메라에서 뻗어나가는 사각뿔 모양의 절두체가 Projection임. 프로젝션은 2가지가 있다.
  • 9.3.1. Perspective Projection
    원근법을 적용하여 모델을 표현. 사람의 눈으로 보는 것과 같음.
  • 9.3.2. Orthograpic Projection
    프로젝션 안의 모든 모델들을 원근감 없이 표현. 왜곡이 없기 때문에 압축해서 보여주는 느낌이 듬

---

10. MVP 매트릭스의 사용 예시

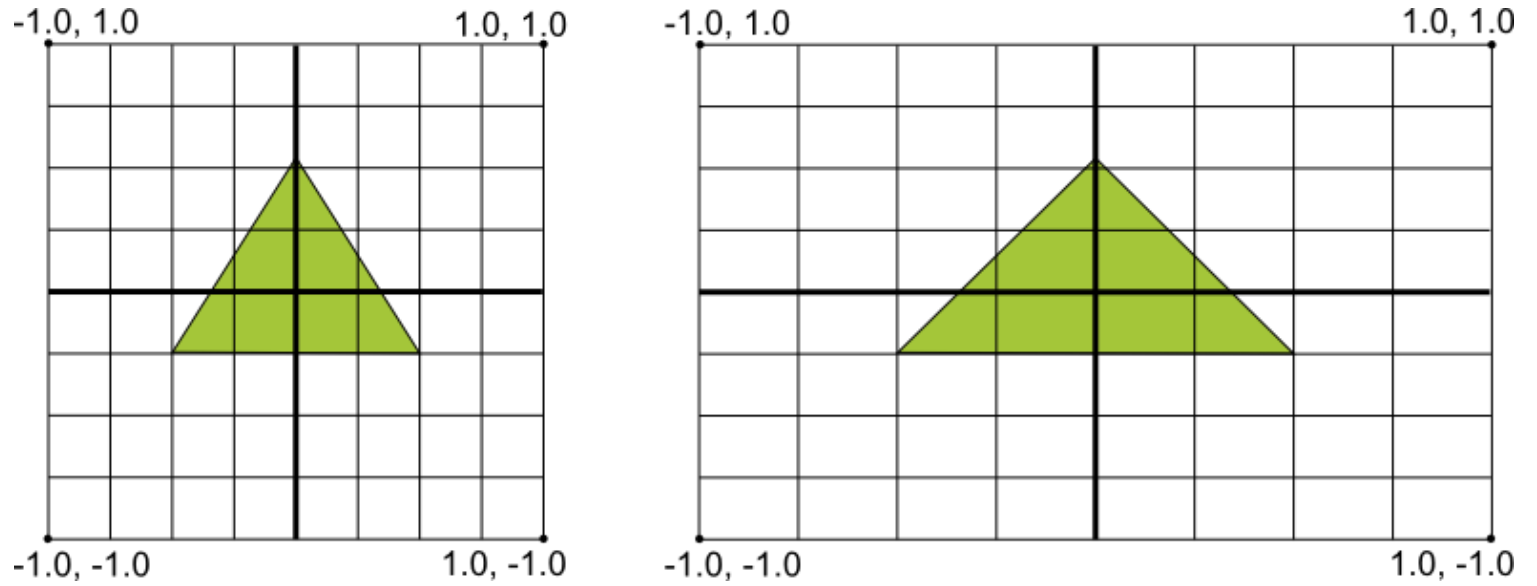
OpenGL의 기본적인 좌표계를 가로가 넓은 안드로이드 스크린 비율에 매핑시 오른쪽 처럼 왜곡이 발생함. MVP 매트릭스로 이 왜곡을 교정 할 수 있다.

• 10.1. Model
  삼각형이 원점에 위치하므로 Model을 움직일 필요가 없음 > 단위행렬 지정.

  private final float[] modelMatrix = new float[16];
  Matrix.setIdentityM(modelMatrix, 0);

• 10.2. View
  카메라도 원점에 있으면 삼각형을 보기 힘드므로 z 축으로 일정거리 멀어져야 함.

  private final float[] viewMatrix = new float[16];
  Matrix.setIdentityM(viewMatrix, 0);
  Matrix.setLookAtM(viewMatrix, 0,
           0.0f, 0.0f, -2.0f,
           0.0f, 0.0f, 0.0f,
           0.0f, 1.0f, 0.0f
  );

  setLookAtM 파라미터 분석

  Matrix.setLookAtM(매트릭스, 매트릭스 offset , 
    		카메라위치(eye), 카메라위치(eye), 카메라위치(eye),
    		카메라 시선(center), 카메라 시선(center), 카메라 시선(center),
    		카메라 업(up), 카메라 업(up), 카메라 업(up),
  	);

따라서 예시의 경우 카메라의 위치를 z축으로 -2.0f만큼, 카메라를 y축 방향으로 1.0f 만큼 위로 올린거라 보면 된다.

• 10.3. Projection
  선택사항이나 일반적인 Perspective로 지정.

  private final float[] projectionMatrix = new float[16];
  Matrix.setIdentityM(projectionMatrix, 0); 
  float aspectRatio = (float) width/ height; // 가로 세로 비율을 구함
  Matrix.perspectiveM(projectionMatrix, 0 , 60, aspectRatio, 1, 7);

  perspectiveM 분석

  Matrix.perspectiveM(매트릭스, 매트릭스 offset , 
  		시야폭, 화면비율, 
  		카메라가 보는 거리 최소값, 카메라가 보는 거리  최대값
  );

• 10.4. MVP 적용

  • 10.4.1. MVP 계산
    mvp = p v m (곱하는 순서 중요함)
    Matrix.multiplyMM(vpMatrix, 0, projectionMatrix, 0, viewMatrix, 0);

  • 10.4.2. 정점쉐이더에 적용

    uniform mat4 uMVPMatrix;
    attribute vec4 vPosition;
    ...
    void main() {
    	...
     	gl_Position = uMVPMatrix * vPosition;
    }

---

Ref.
https://www.charlezz.com/?p=936
https://www.charlezz.com/?p=934
https://www.charlezz.com/?p=960
https://medium.com/@NovaWoo/opengl%EC%9D%84-%EC%9C%84%ED%95%9C-3d-%EA%B8%B0%EB%B3%B8-%EA%B0%9C%EB%85%90-1-1f305105b478