문제 url:
알고리즘 수업 - 알고리즘의 수행 시간 6
문제:
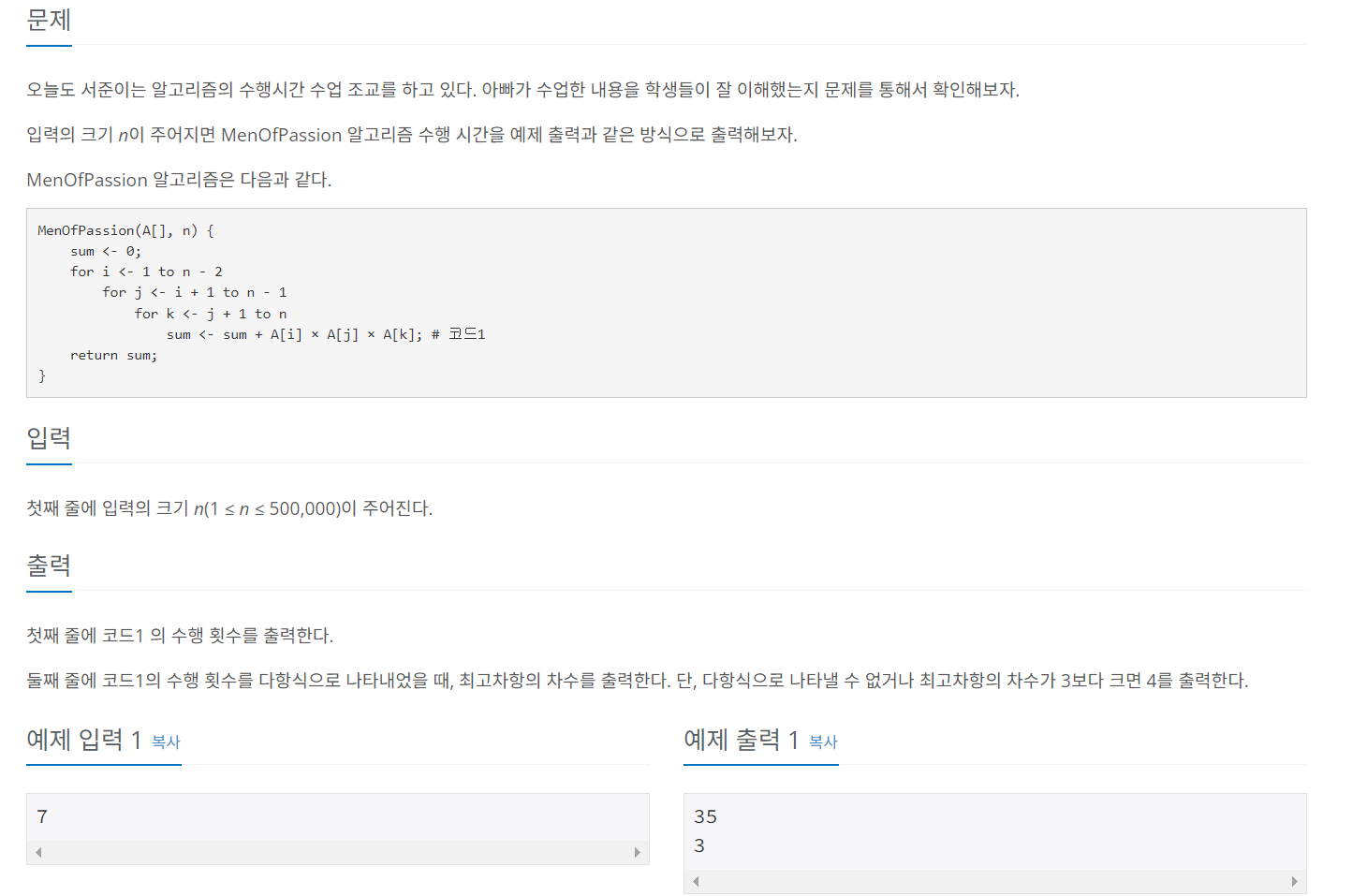
🤔 문제 알아보기
문제의 MenOfPassion 알고리즘을 살펴보면 for문이 3중으로 되어 있는것을 볼 수 있다. 그렇다면 for문의 시간 복잡도는 O(N)이니깐 해당 시간 복잡도는 O(N^3)인 것을 알 수 있다.
시간 복잡도를 구했으니깐, 문제의 수행 횟수를 구해보자
첫 번째 for문은 i = 1부터 n -2까지 반복한다.
두 번째 for문은 j = i + 1부터 n -1까지 반복한다.
세 번쨰 for문은 k = j + 1부터 n까지 반복한다.
이를 계산하면
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 |
|---|---|---|---|---|
| j = 1 + 1 | j = 2 + 1 | j = 3 + 1 | j = 4 + 1 | j = 5 + 1 |
| k = 2 + 1 | k = 3 + 1 | k = 4 + 1 | k = 5 + 1 | k = 6 + 1 |
| 7,6,5,4,3 7,6,5,4 7,6,5 7,6 7 | 7,6,5,4 7,6,5 7,6 7 | 7,6,5 7,6 7 | 7,6 7 | 7 |
| 15 | 10 | 6 | 3 | 1 |
다음과 같이 계산될 수 있다.
처음에는, 해당 숫자들이 1 ~ 15까지 되는데 2, 3, 4, 5씩 늘어나며 누적합을 계산하는 줄 알았다.
1 ~ 3이 되는데 필요한 수: 2
3 ~ 6이 되는데 필요한 수: 3
6 ~ 10이 되는데 필요한 수:4
10 ~ 15이 되는데 필요한 수:5하지만 해당 수를 구하려고 해도 for문이 필요했다. 결국 타 블로그를 참조하니
1부터 n까지의 숫자중 3가지 (i, j, k에서 하나씩 뽑는 방식)를 뽑아 중복이 없고, 순서와 상관없이 선택하는 경우의 수로 구할 수 있었다.
고등학교 때 배우는 [확률과 통계] 순열/ 조합 part에 나오는 내용이다.
수포자인 필자도 이건 알았는데.. 왜 지금은 모를까
코테 준비할 때 양으로 떼우는 것이 어려운 이유가,
이런 수학적 사고방식이 필요하기 때문이라 생각한다.우리는 해당 내용에서 조합의 공식을 사용할 줄 안다면 문제를 풀 수 있다.
n: 최대 몇까지의 숫자를 의미
r: 뽑을 숫자의 개수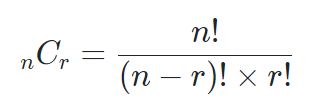
수포자인 필자도 팩토리얼 ! 를 알기 때문에 해당 부분은 설명하지 않고 넘어간다.
즉 이를 공식에 대입하면
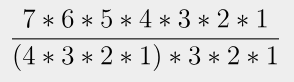
여기서 4 * 3 * 2 * 1은 없앨 수 있으니 값은 아래와 같이 된다.
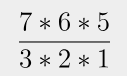
이를 코드화 시킨다면 아래와 같을 수 있다.
🐱👤 실제 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
System.out.println((n * (n-1) * (n-2)) / 6);
System.out.println(3);
}
}
🤢 회고
순열과 조합을 알았으면, 한번에 맞췄을 문제였다. 알고리즘을 공부하면서 이렇게 중,고등학교때 수학을 등한시 한것이 굉장히 후회된다..
그래서 순열과 조합을 따로 파트로 나누어 다시 공부해보고자 한다.
[확률과 통계] 순열과 조합 <- 순열과 조합을 정리한 부분