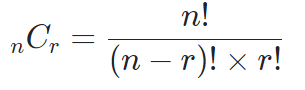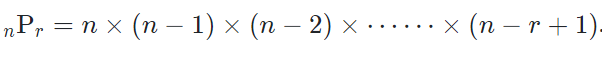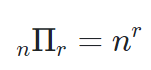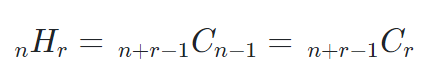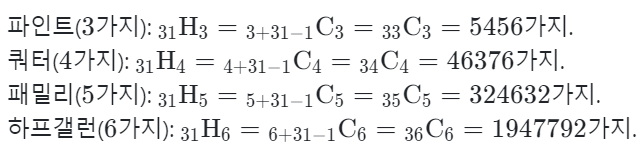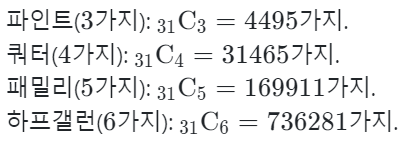🚑 잠시 쉬어가기
블로그에 새로운 세션이 생겼다!! 두둥. 수학 태그를 만들면서 이제부터 필수적인 수학적 지식을 여기에 담아보고자 한다.
추후 나중에 AI관련 공부를 할 때에도 해당 세션에 많은 글을 적어보고자 하니, 기대가 된다
🤔 들어가기 앞서
순열과 조합은 너무 비슷해서 유형을 잘 구분해야 한다.
👀 순열
순열에서 가장 중요한 것은 뽑는 순서에 따라 결과가 달라진다. 그래서 뽑는 순서가 중요한 가 그렇지 않은가를 잘 판단해야 한다.
정의:
서로 다른 n개의 원소에서 r(0 < r <= n 일때) 중복없이 순서와 상관 있게 선택하는 경우의 수
공식:
해당 값을 간략화 하면 아래와 같다.
순열의 대표적인 예시를 얘기하면,
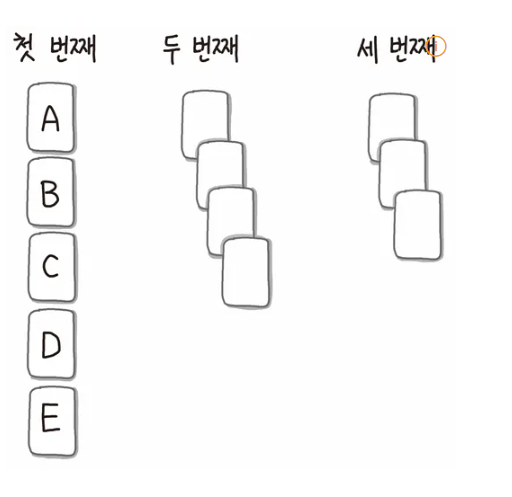
5장의 카드에서 3장의 카드를 골라 순서대로 나열해 세 자리의 문자를 만드는 경우의 수를 생각해보자.
첫 번쨰 자리에는 5개가, 두 번째에는 한 개를 뺀 4개가, 세 번쨰에는 두 개를 뺸 3개가 위치할 수 있다.
👀 중복 순열
중복 순열은 서로 다른 n개 중에 r개를 순서에 상관 있게 뽑는데, 중복을 허락하여 뽑는 것을 말한다.
공식:
여담으로 0개 중에 0개를 뽑는 경우의 수는 1개라고 한다.
예시:
0~9까지의 범위를 가진 3자리 자물쇠가 가질 수 있는 경우의 수
10 ^ 3으로 총 1,000
✨ 조합
조합이란 n개의 원소를 갖는 집합에서 r개의 원소를 선택하는 것 혹은 선택의 결과로 정의된다.
어떤 순서로 원소를 선택했는지 중요하지 않기 때문에, 순열과 다른 개념
정의:
서로 다른 n개의 원소 중 r개를 중복 없이 순서와 상관 없이 선택하는 경우의 수이다.
공식:
예시:
A,B,C,D,E의 5장의 카드중 3장의 카드를 뽑는 경우의 수
5 * 4 * 3 * 2 * 1 / (2 * 1) * 3 * 2* 1총 10가지가 나온다.
중복 조합
정의:
서로 다른 n개의 원소 중 r개를 순서에 상관없이 뽑는데, 중복을 허락할 때의 경우의 수
공식:
여기에 재미난 값이 있어서 가져와봤다.
베스핀라빈스의 31가지 아이스크림을 중복을 허용하고 고른다면, 총 경우의 수는 다음과 같다.
만약 중복을 허용하지 않는 조합이라면, 다음과 같다고 한다.
😊 간단 정리
순열은 서로 다른 n개의 조합 중 중복 없이 순서를 고려해서 r번 뽑는 것
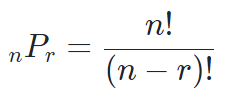
조합은 서로 다른 n개의 조합 중 중복 없이 순서를 고려하지 않은 채 r번 뽑는 것