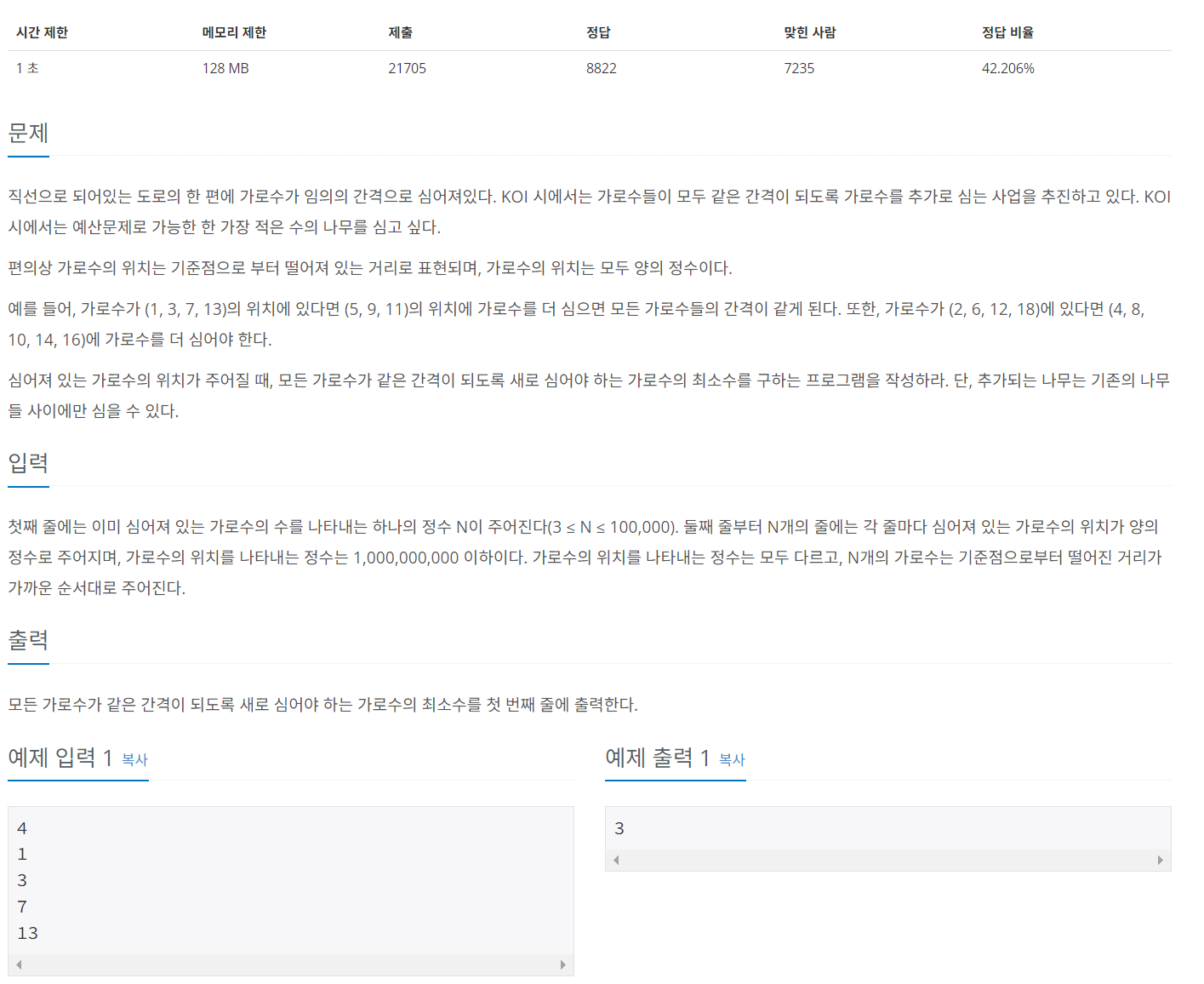
문제 url:
가로수
문제:
🤔 문제 알아보기
먼저, 필자는 계산을 잘못해서 결국... 잘못된 방법으로 문제를 풀다 답지를 보게 되었다.
하지만, 접근법에 대해서는 맞았었기에 접근법에 대해서 설명을 하자면,
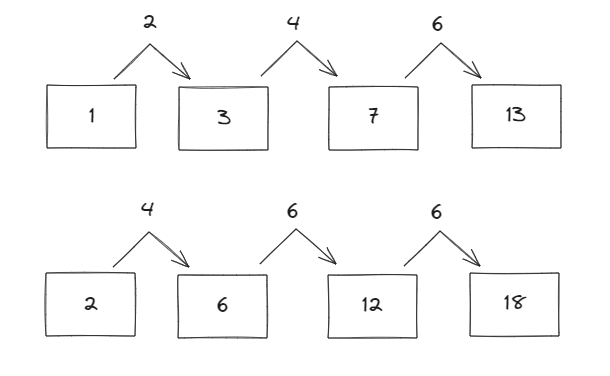
이번 문제의 TC를 그린 그림이다. 인덱스 i와 인덱스 i-1의 차이를 적어놨는데, 유심히 보면 뭔가 떠오르는게 있지 않은가?
즉, 이번 문제도 최대 공약수로 문제를 풀 수 있다.
먼저 첫 번째 TC를 살펴보면, 2의 배수로 간격이 벌어지는 것을 볼 수 있는데, 만약 가장 큰 수인 6을 간격을 잡으면, 1 ~ 3은 아예 성립이 되지 않는다. 이는 4도 마찬가지이다. 그렇다면 2는 어떨까? 2를 하게 되면 1, 3, 5, 7, 9, 11, 13으로 일정한 간격으로 나눌 수 있다.
그렇다면 두 번째 TC를 살펴보자, 간격이 4, 6, 6 만큼 차이가 나타나는데,
가장 큰 간격인 6을 기준으로 하게 되면 2 ~ 6이 성립되지 못해 할 수 없고,
4를 기준으로 해보자. 그렇게 되면 6 ~ 10 , 10 ~ 14가 되어야 하는데, 이미 12가 존재한다.
문제 조건을 잘 읽어보면, 이미 존재하는 가로수 사이에 가로수가 추가되며 모든 가로수는 일정한 간격을 가지고 심어야 한다고 한다.
해당 기준에 의해서 4 역시 하지 못한다. 그렇다면 해당 간격을 모두 포함할 수 있는 간격을 찾아야 하는데, 이는 4, 6, 6을 d로 나눴을 때 모두 나머지가 0인. 즉 나누어 떨어질 수 있는 값이어야 한다는 것이다.
그래서 이때, 차이의 최대공약수를 구해서 그만큼 간격마다 가로수를 심을 수 있는 것이다.
🐱👤 실제 코드
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] arr= new int[N];
for(int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
int gcd = 0;
for(int i = 1; i < N; i++) {
gcd = gcd(arr[i] - arr[i-1], gcd);
}
System.out.println((arr[N-1] - arr[0]) / gcd + 1 - arr.length);
}
static int gcd(int a, int b) {
while(b != 0) {
int r = a % b;
a = b;
b = r;
}
return a;
}
}
코드를 보면 더 이해가 빠를것이다.
여기서 핵심 로직을 풀이하자면,
1) gcd 로직
int gcd = 0;
for(int i = 1; i < N; i++) {
gcd = gcd(arr[i] - arr[i-1], gcd);
}유클리드 호제법 풀이를 간략히 설명하면,
gcd(a,b) = gcd(b, r)※여기서 r은 a % b이다.
해당 식이 성렵하는데, 즉 a,b의 최대공약수는 b,r의 최대공약수와 같다.
여기서 r이 0이 될 때까지 반복하면 결국 gcd(a,b)의 최대공약수는 b과 같다
유클리드 호제법이란?
처음 gcd는 r로 들어가는데, 여기서 r이 0이 되면, gcd(b,r) -> b가 최대공약수가 된다고 했다. 그 값을 gcd에 초기화 시켜주고 다음 값도 비교하면 gcd를 초기화 시켜준다.
그러면 첫 번째 TC를 기준으로 gcd를 구해보면
※간격 차는 2, 4, 6이다
gcd(2, 0) -> gcd(4,2) / gcd(2,0) -> gcd(6,2) / gcd(2,0) 즉, 최대 공약수 2를 구할 수 있는 것이다.
2) 간격 간 새롭게 추가할 가로수 개수
System.out.println((arr[N-1] - arr[0]) / gcd + 1 - arr.length);해당 코드를 보고 놀랬었다.. '왜 이렇게 생각하지 못했을까' 하고
일단 첫 번째 TC를 기준으로 설명해보면 ※ 1, 3, 7, 13
13 - 1 / gcd(2) = 6 + 1
즉, 해당 간격안에 7개의 가로수를 심을 수 있다.
※뒤에 +1을 해준 이유는, 첫 번째 가로수와 마지막 가로수 사이의 거리에 포함되지 않은 첫 번째 가로수를 고려해서 1을 더해주는 것이다.
손으로 구해보면 1, 3, 5, 7, 9, 11, 13 이렇게 나올 수 있다.
그후 -arr.length를 하는데, 이는 이미 심어진 가로수의 개수와도 같은 값이다.
그렇다면 해당 풀이를 종합하면, 1, 3, 7, 13 사이에는 7개의 가로수를 심을 수 있으며, 그중 4개가 심어져 있기 때문에 총 3개의 가로수를더 심을 수 있다.
🤢 회고
해당 문제를 한번에 풀지 못해 약간 서러웠다... tc를 잘못봐서 아예 잘못된 길로 가버린...
문제를 꼼꼼하게 읽는게 얼마나 중요한 것인지 또 복기한 문제였다.