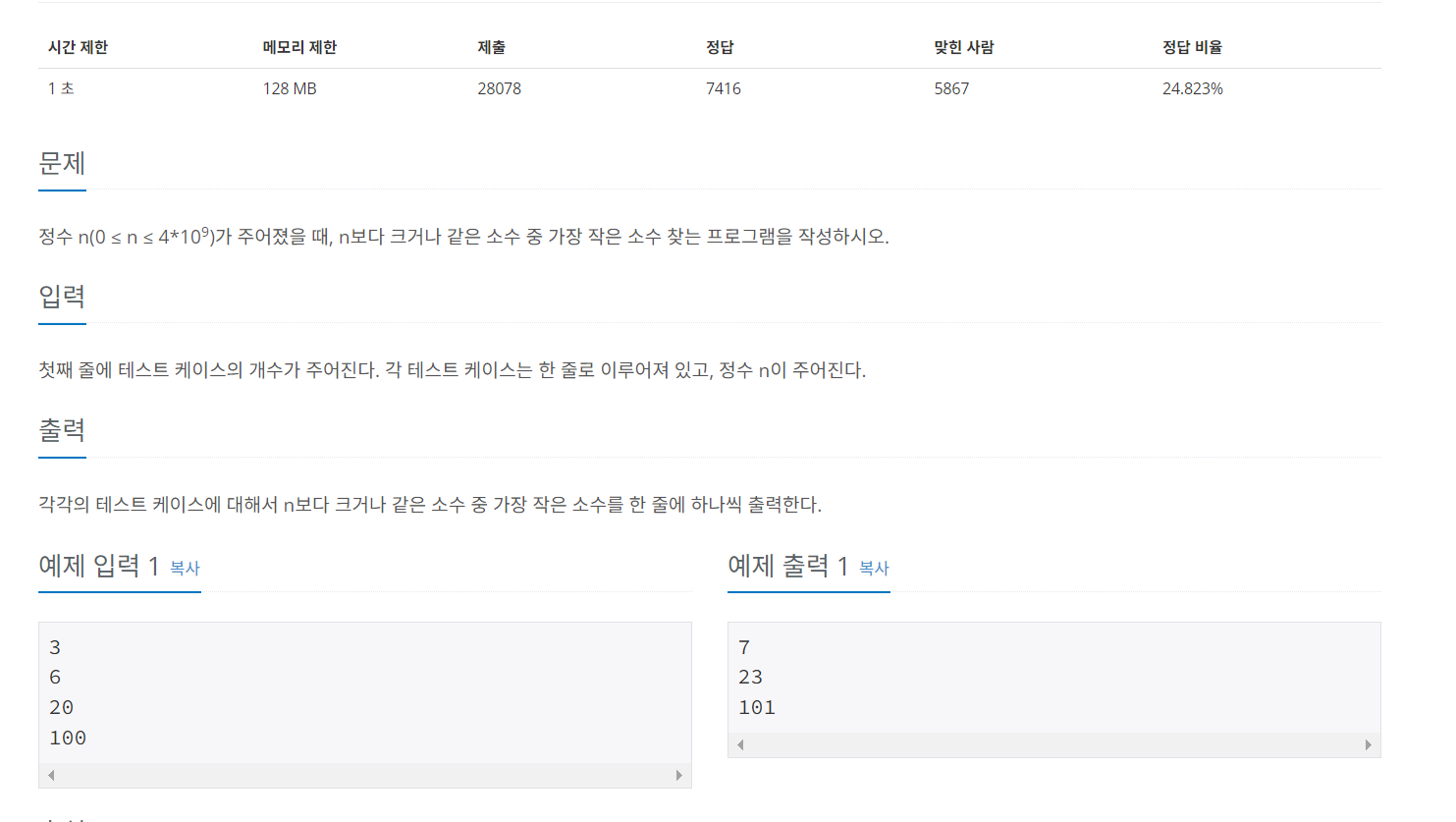
문제 url:
다음 소수
문제:
🤔 문제 알아보기
소수문제는 나름 자신있다고 생각했는데, 그렇지 않았다..
암튼 문제를 같이 알아보자,
전형적인 소수문제이다. 하지만 정수n은(0<= n <= 40억)까지 찾아야 하는 수이다.
즉, int형으로는 오늘밤 때려죽어도 못푸는 문제이다. 그래서 우리는 정수타입중 가장 큰 범위를 가진 long으로 풀고자 한다.
여기까지는 not bed~ 여긴 침대가 아니다.
가장 문제가 무엇이냐면, 각 tc에 대한 값을 받았을 때, 해당 값과 같거나 큰 소수중 가장 작은 소수를 찾아야 한다.
한마디로 입력 받은 값보다 큰 소수를 찾을 수 있는 로직이 구현되어야 한다는 것이다.
필자는 여기서 막혔었다. 본인이 생각한 것보다 구현능력이 생각보다 떨어져서 놀랫다
또한 입력값이 0보다 크기 때문에 0과 1같은 경우 소수가 아닌점을 꼭 명시하고 예외처리를 진행해줘야 한다.
필자는 이번 문제를 브루트포스 형태로 풀었다. 하지만 시간 제한은 1초
총 1억번의 연산안에 해당 문제를 풀 수 있어야 한다.
그러나, 최대 40억자리까지 사용하며, 40억 이상의 소수를 찾으려면 40억 + a라는 소리이다.
우리가 아는 브루트포스 형태로 풀게 된다면 때려죽어도 시간제한을 못 벗어날 것이다.
for(int i = 0; i < 40억; i++) {
if(prime % i !=0) {
prime은 소수입니다.
}
}이런식을 말한다. 하지만! 네이버에 소수를 치고 검색해보면 다음과 같은 식을 볼 수 있는데,
소수란?
2 <= p <= sqrt(n)인 범위에 있는 모든 소수 p로 n을 나누어 보아, 나누어 떨어지지 않으면 소수이고, 나누어 떨어지면 합성수이다.여기서 sqrt는 루트값인데, 네이버에서도 친절하게 설명해준다.
그렇다면 왜 sqrt까지만 반복하면 되는 것인가?
그 이유에 대해서는 아래의 링크를 통해 알아 볼 수 있다.
백준 1978번 소수찾기
그럼에도 누르지 않은 당신! 을 위해서 간략히 설명하겠다.
소수 11를 이용해 간략히 설명해보겠다.
11 % 1 = 0 --- > 소수(1과 자기자신만 공약수일 경우 소수이다)
11 % 2 = 9 --- > 소수아님
11 % 3 = 2 --- > 소수아님
11 % 4 = 7 --- > 소수아님
11 % 5 = 1 --- > 소수아님
11 % 6 = 5 --- > 소수아님
11 % 7 = 4 --- > 소수아님
11 % 8 = 3 --- > 소수아님
11 % 9 = 2 --- > 소수아님
11 % 10 = 1 --- > 소수아님
11 % 11 = 0 --- > 소수이렇게 1과 11로만 나누어 떨어지기 때문에 소수이다.
입력값 C에 대해서 C = A X B로 이루어진 합성수이다.그래서 1<= A,B <= C와 같은 부등호를 가질 수 있는데,
만약 여기서 A or B가 C의 제곱근보다 커지면 해당 값이 모순이 생길 수 있다.
11의 제곱근은 3.31인데, 만약 A나 B가 3.31보다 큰 수라면
A X B > C의 식을 가지게 되며 위에서 봤던 수식이 성립되지 않는다.그래서 결론을 낸다면
합성수 C = A X B에서 A 또는 B중 적어도 하나는 √C보다 작거나 같다.
그렇기 때문에 √C만큼 반복을 하면 되는 것이다.
이렇게 풀게 된다면 우리는 시간복잡도 O(logN)으로 대략 63246 연산이 가능하다.
풀이를 함께 보자
🐱👤 실제 코드
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sbd = new StringBuilder();
int N = Integer.parseInt(br.readLine());
for(int i = 0; i < N; i++) {
long prime = Long.parseLong(br.readLine());
// 입력받는 prime은 0부터 시작한다고 했으니, 0과 1 이상의 소수는 2라서 2 출력
if(prime == 0 | prime == 1 ) {
sbd.append(2).append("\n");
continue;
}
while(true) {
long cnt = 0;
for(long j = 2; j <= Math.sqrt(prime); j++) {
if(prime % j ==0) {
cnt++;
break;
}
}
if(cnt == 0) {
sbd.append(prime).append("\n");
break;
}
prime++;
}
}
System.out.println(sbd);
}
}
주요 로직을 설명하자면,
while(true) {
long cnt = 0;
for(long j = 2; j <= Math.sqrt(prime); j++) {
if(prime % j ==0) {
cnt++;
break;
}
}
if(cnt == 0) {
sbd.append(prime).append("\n");
break;
}
prime++;
}이 부분은 만약 입력받은 prime수가 소수가 아니거나 더 큰 소수값이 존재하지 않을 때, 즉 현재 값이 소수가 아닐 때 입력받은 prime에 1씩 더해서 구하는 로직이다.
그래서 이를 위해 cnt가 0이라면 소수이기 때문에 해당 prime을 출력한다.
필자가 정신이 몽롱해서 이런 착각을 한 트러블 슈팅이 있다!
아니.... prime % j ==0 에서 j가 prime과 같으면 당근 0이죠...
근데 아차차 반복횟수가 prime 제곱근인걸 깜빡했다!!
맞다. 때려죽어도 j는 prime과 같은 값을 가질 수 없다.
이 부분 때문에 또 많은 시간과 불필요한 로직을 남기게 되었다...
제곱근을 하는 이유는 위에서 설명했기에 넘어간다.🤢 트러블 슈팅
진짜 머리 터질뻔한 예외가 있었는데, 바로 NumberFormatException이다.
분명... 모든 코드가 완벽하고, 로직도 다 이해했는데 왜 예외가 발생하지..
처음부터 타입을 long으로 시작하고 확인까지 다 했는데.
근데 알고보니 입력을 받는 Integer.parseInt(br.readLine()) 이것은 int형으로 받는 것이기 때문에 큰 수를 받으면 String으로 변환되어 입력된다.
이 것을 가장 극단값인 40억을 넣고 나서야 알아버렸다.
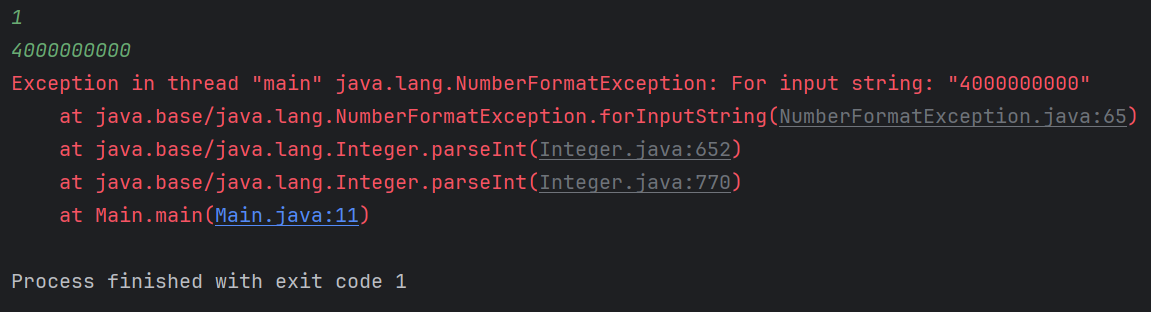
꼭 기억하자, int형타입을 int형 범위를 넘어서 받으면 String으로 받는다는 것을
또 반드시 Long 타입을 받을 때는 Long.parseLong 으로 받아야 한다.
😒 리팩토링
타 블로그를 보니 다른 방법이 있어서 한번 공부를 해보았다.
바로 BigInteger인데
BingInteger는, int, long, Integer, Long과 달리 문자열 형태로 숫자를 처리하므로 아무리 큰 수라도 담을 수 있다.
즉, 무한에 가까운 수를 입력받을 때 좋은 방법이다.
그렇다면, 왜 BigInteger를 쓰는가?
만약 int나 long처럼 타입의 표현 범위를 넘어선 값이 들어오면, 0 또는 에러나 원치않는 값이 출력될 수 있다. 그럴 때 BigInteger는 문자열로 받기 때문에 큰 수를 받을 수 있어 사용한다.
🐱👤 리팩토링 코드 Using BigInteger
import java.io.*;
import java.math.BigInteger;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sbd = new StringBuilder();
int N = Integer.parseInt(br.readLine());
for(int i = 0; i < N; i++) {
long prime = Long.parseLong(br.readLine());
// 숫자를 문자열로 받기 때문에 반드시 문자열로 변환시켜줘야 한다.
BigInteger primeNumber = new BigInteger(String.valueOf(prime));
// 해당값이 만약 소수라면 true,
if(primeNumber.isProbablePrime(10)) {
sbd.append(primeNumber).append("\n");
} else {
sbd.append(primeNumber.nextProbablePrime()).append("\n");
}
}
System.out.println(sbd);
}
}
짧게 설명하면, BIgInteger는 Math 클래스 안에서 import하여 객체로 사용할 수 있으며 숫자형태인 문자열을 입력해서 사용한다.
BigInteger.isProbablePrime(10)은 소수이면 true 아니면 false를 반환하는데,
여기서 10을 넣는 이유는
해당 메서드는 certainty라는 확실성을 나타내는 인수값을 받는다.
여기서 값이 소수인지 아닌지를 나타내는 확률은 1-(1/2)^certainty 를 가지는데, 10인 경우의 확률은 0.9990234375 정도 된다고 설명한다. 암튼 큰 수도 거의 정확하게 판별할 수 있다고 본다.
필자와 같이 봐도 잘 모르는 분은 같이 외우는 쪽으로,, 가도록 하자
그 다음, BigInteger.nextProbablePrime() 메서드는 입력값 다음 소수를 반환하는 메서드로 이번 문제가 추구하는 바를 단 한 줄의 메서드로 나타낸 것이다.

아쉽게도, BigInteger는 많은 메모리와 시간이 걸려 효율적이진 못하다.
해당 부분에 대해서는 BigInteger를 조금 더 연구를 해봐야 겠다.