[탐색] 이진 탐색(Binary Search)를 살펴보자

hansung's·2024년 3월 13일

알고리즘 탐색

🤔 이진 탐색이란?

들어가기 앞서 이진 탐색 혹은 이분 탐색(Binary Search)에 대해서 간략히 설명하자면,
순차적 탐색보다 빠르게 탐색하기 위해 반으로 분리해 탐색하는 방법

그렇다면 순차적 탐색은 무엇인가?

정렬된 배열에서 특정 원소값을 찾기 위해 인덱스 0부터 차레대로 탐색
누락되는 곳 없이 순차적으로 탐색한다.
최악의 경우 시간 복잡도: O(n)
- 리스트의 모든 요소를 다 확인하기에 최악의 경우 리스트 길이(n)에 비례함

이진탐색은 무엇인가?

정렬된 배열에서 특정 원소값을 찾기 위해 중앙값을 기준으로 비교하며 탐색
탐색하는 값이 있을 때까지 인덱스를 옮기는데, 없으면 반복 종료
인덱스 left와 right가 정해질 때마다 탐색 범위가 절반씩 줄어든다.
최악의 경우 시간 복잡도: O(log n)
- 탐색 범위가 절반씩 줄어드는 과정에서 로그 시간복잡도를 가짐
이분 탐색을 사용하기 위해서는 리스트가 반드시 정렬되어 있어야 한다.
- 정렬만 되어 있다면, 많은 데이터에도 빠르게 값을 찾을 수 있다.

😎 이진탐색의 구동 원리

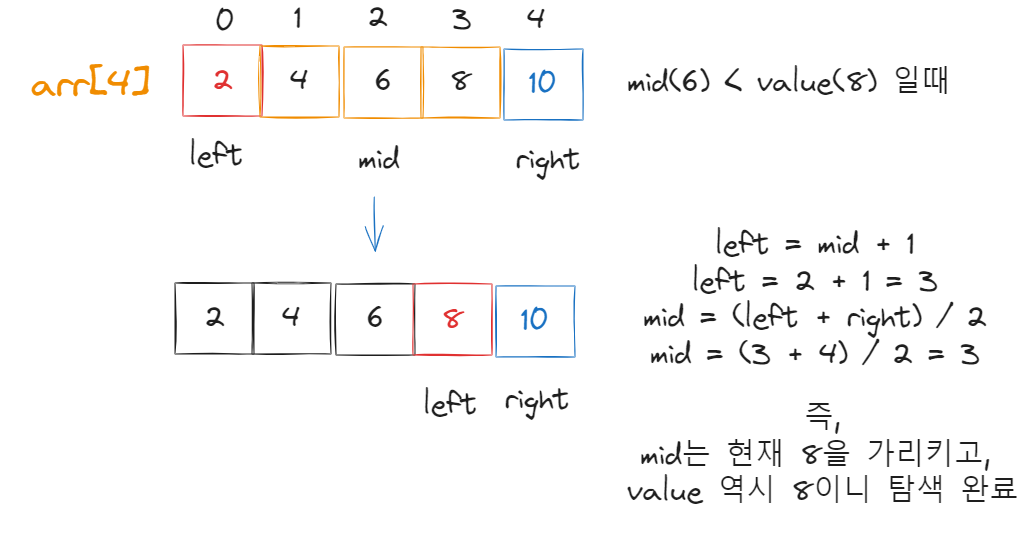
길이가 N인 정렬된 배열 혹은 리스트가 존재한다고 가정하자 그럼
left_idx = 0
right_idx = N-1
mid_idx = (left_idx + right_idx) / 2 의 인덱스 값을 가진다.

그 후, mid_idx의 값과 찾고자 하는 값을 비교해서
mid_value < search_value 라면 중앙값보다 크기 때문에
left_idx = mid_idx + 1을 하며 범위를 좁혀 나간다.

간략히 그림으로 보면 이렇게 구할 수 있다.

이를 정리해서 설명하면

mid < value:
Value가 중앙값보다 크다면 left를 mid +1로 만들어 줌 (왼쪽 세션을 버림)

mid > value:
Value가 중앙값보다 작다면 right를 mid -1로 만들어 줌 (오른쪽 세션을 버림)

mid == value:
value와 중앙값이 일치하기 때문에 return;

🐱‍👤 실제 코드 1.) 반복문 사용

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int[] arr;
    static int count = 0;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int Value = Integer.parseInt(br.readLine());

		//현재 arr배열은 정렬된 상태이다.
        arr = new int[]{2,4,6,8,10}; 

        Boolean is_exist = binary_search(Value);

        if(is_exist) {
            System.out.println("존재합니다. 탐색까지 반복 횟수는 : " + count);
        } else {
            System.out.println("미존재합니다. 탐색까지 반복 횟수는 : " + count);
        }
    }

    static Boolean binary_search(int Value) {
        int left_idx = 0;
        int right_idx = arr.length - 1;

        while(left_idx <= right_idx) {
            count++;
            
            // 나누기 2를 해줌으로써 절반만 탐색할 수 있는 것이다.
            int mid_idx = (left_idx + right_idx) / 2;
            int mid = arr[mid_idx];

            if (mid < Value) { // 왼쪽을 버려야 한다. 버린 후 mid 초기화 하고 다시 검증
                left_idx = mid_idx + 1;
            } else if(mid > Value) { // 오른쪽을 버려야 한다. 버린 후 mid 초기화 하고 다시 검증
                right_idx = mid_idx -1;
            } else { // 현재 Value와 Mid가 일치함. 즉 탐색이 완료되었다.
                return true;
            }
        }

        return false;
    }
}

🐱‍👤 실제 코드 2) 재귀 함수 사용

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int[] arr;
    static int count = 0;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int Value = Integer.parseInt(br.readLine());

        arr = new int[]{2,4,6,8,10};
        int left_idx = 0;
        int right_idx = arr.length - 1;

        boolean is_exist = binary_search(arr, Value, left_idx, right_idx);

        if(is_exist) {
            System.out.println("존재합니다. 탐색까지 반복 횟수는 : " + count);
        } else {
            System.out.println("미존재합니다. 탐색까지 반복 횟수는 : " + count);
        }
    }

    static boolean binary_search(int[] arr, int Value, int left_idx, int right_idx) {
        if(left_idx > right_idx) return false;

        int mid = (left_idx + right_idx) / 2;

        if (arr[mid] < Value)
            return binary_search(arr, Value, mid+1, right_idx);
        else if(arr[mid] > Value)
            return binary_search(arr, Value, left_idx, mid-1);
        else
            return true;

    }
}

작은 트러블 슈팅을 기록한다면, 재귀함수를 사용할 때, 반드시 return을 앞에 적어줘야 한다.

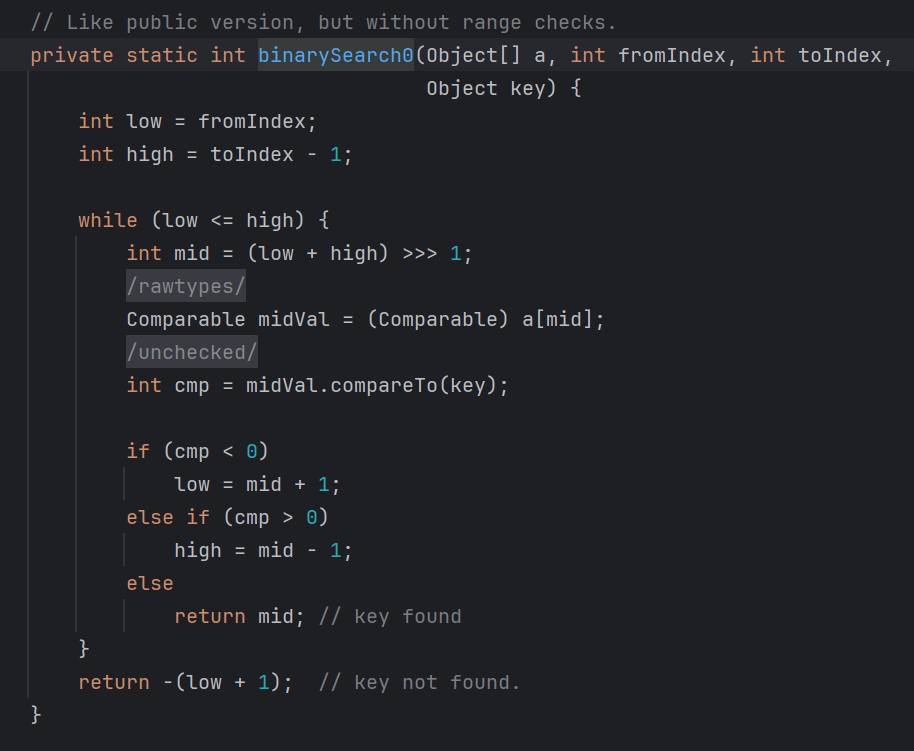
👏 문자열 이진 탐색

문자열을 이진 탐색할 때는, Arrays.binarySearch()함수를 이용합니다.
여기에서도 반드시 배열이 정렬되어 있어야 합니다.

문자열 배열을 탐색할 때에는 위의 로직을 사용하게 된다.
이전에 봤던 내용과 유사하게 배열과 찾고싶은 key값을 파라미터로 받는다.

binarySearch 로우 코드를 살펴보면 return mid와 return -(low +1)을 볼 수 있다.
즉 mid는 현재 인덱스 위치를 의미하며, 만약 키값이 존재한다면 해당 인덱스를 반환
그렇지 않으면, 음수를 반환하게 된다.

예시 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        // 출력시 개수를 확인할 변수 정의
        int count = 0;

        String[]N_arr = new String[N];
        for(int i = 0; i < N; i++) {
            N_arr[i] = br.readLine();
        }

        Arrays.sort(N_arr);

        for(int i = 0; i < M; i++) {
            int result = Arrays.binarySearch(N_arr, br.readLine());
            if (result > 0) {
                count++;
            }
        }
        System.out.println(count);

    }
}