[알고리즘/Java] 이분 탐색 / 이진 탐색 (Binary Search)

✔ 목차

1. 이분 탐색이란?
2. 이분 탐색 방법
3. 이분 탐색 구현 - Java
4. 시간복잡도

---

🔎 이분 탐색이란?

이분 탐색은 이진 탐색, Binary Search 라고도 한다. 순차적 탐색보다 빠른 탐색을 위해 나온 탐색 방법으로 실제로 이분 탐색의 시간복잡도가 순차적 탐색보다 낮다.

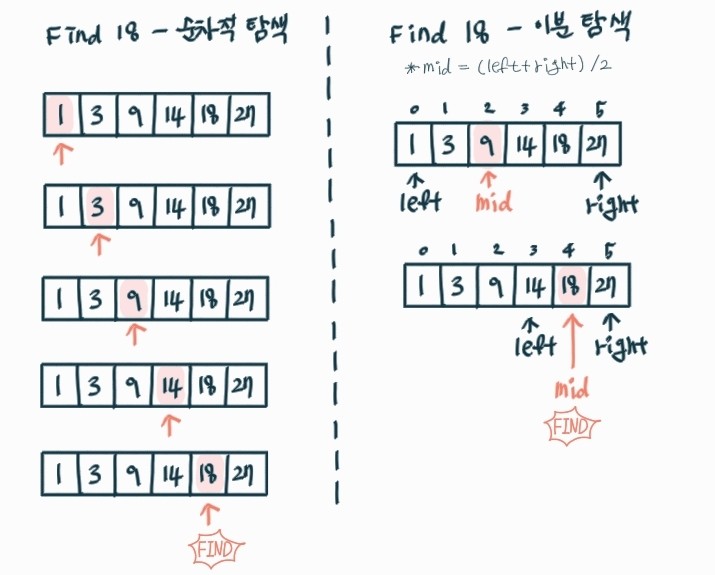
순차적 탐색

• 정렬된 배열 안에서 특정 원소를 찾기 위해 인덱스 0부터 차례로 탐색
• 원소를 건너뛰는 일 없이 순차적으로 탐색
  
  

이분 탐색

• 정렬된 배열 안에서 특정 원소를 찾을 때 인덱스 i부터 j의 중간값과 비교
• 중간값이 찾는 원소가 아니라면 인덱스 i와 j 다시 정해줌
• 인덱스 i와 j의 정할 때 마다 탐색 범위 반으로 줄어듦

---

🔎 이분 탐색 방법

1. 처음 범위는 인덱스 0부터 끝까지이다. 이 때 중간 인덱스를 mid로 한다.

2. mid의 값와 찾는 원소를 비교한다.
   2-1) 찾는 원소와 mid의 값이 같다면 탐색 종료한다.
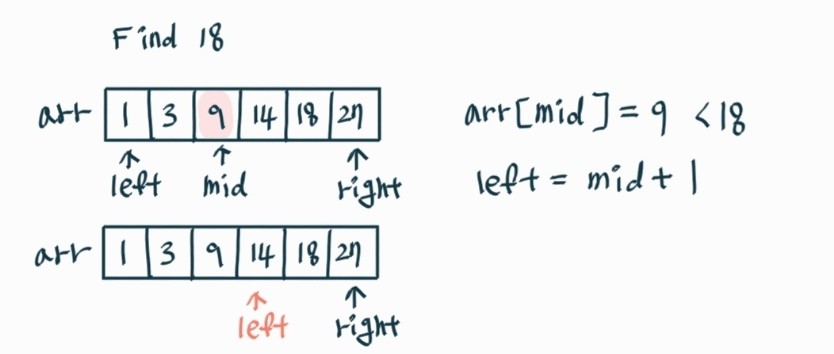
   2-2) mid의 값 < 찾는 원소 일 때 left는 mid + 1로 하여 2)를 다시 반복한다.
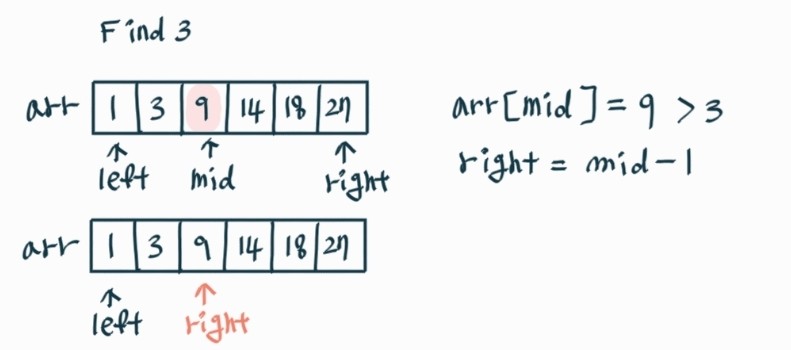
   2-3) mid의 값 > 찾는 원소 일 때 right는 mid - 1 로 하여 2)를 다시 반복한다.

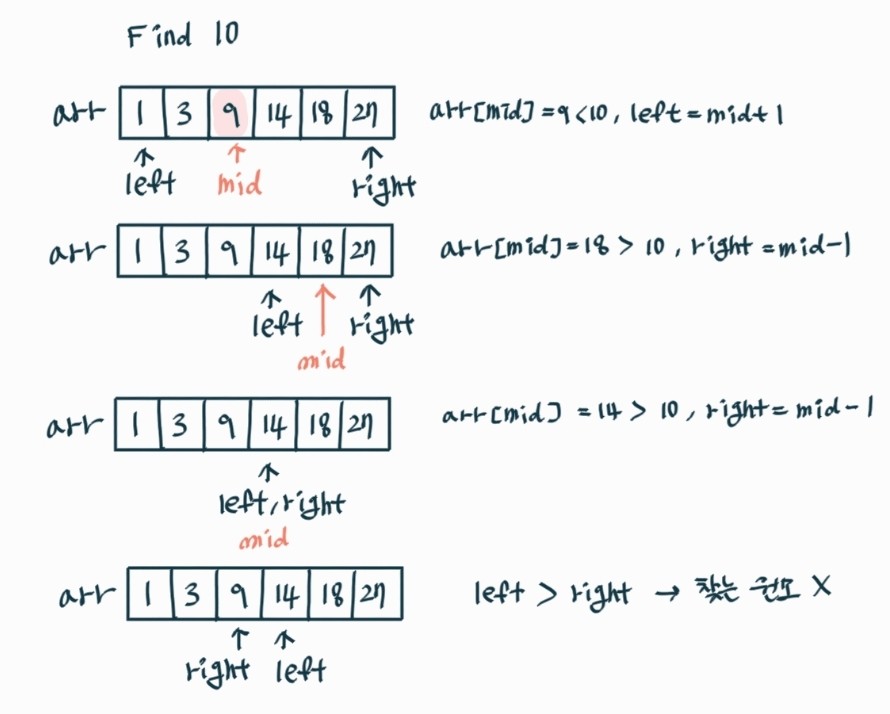
3. 만약 right > left가 된다면 해당 배열에 찾는 원소가 없는 것이다.

2-2) 그림

---

2-3) 그림

---

3. 그림

---

💻 이분 탐색 구현(Java)

1. 반복문으로 구현

	public static boolean BSearch(int[] arr, int n) {
		int left = 0;
		int right = arr.length - 1;
		int mid;

		while (left <= right) {
			mid = (left + right) / 2;
			if (arr[mid] < n) left = mid + 1;
			else if (arr[mid] > n) right = mid - 1;
			else return true;
		}
		return false;
	}

2. 재귀로 구현

	public static boolean BSearchRecursive(int[] arr, int n, int left, int right) {
		if(left > right) return false;
		
		int mid = (left + right) / 2;
        
		if (arr[mid] < n) 
        	return BSearchRecursive(arr, n, mid +1, right);
		else if (arr[mid] > n) 
        	return BSearchRecursive(arr, n, left, mid - 1);
		else 
        	return true;
		
	}

---

⏰ 시간복잡도

• 순차적 탐색: 최악의 경우 배열의 끝까지 탐색해야한다. -> O(n)

• 이분 탐색: 범위를 새로 정할 때 마다 탐색 범위는 1/2씩 줄어든다. -> O(log n)

탐색 기법	시간복잡도
순차적 탐색	O(n)
이분 탐색	O(log n)

---