Mobile Robot kinematics
1. Translation
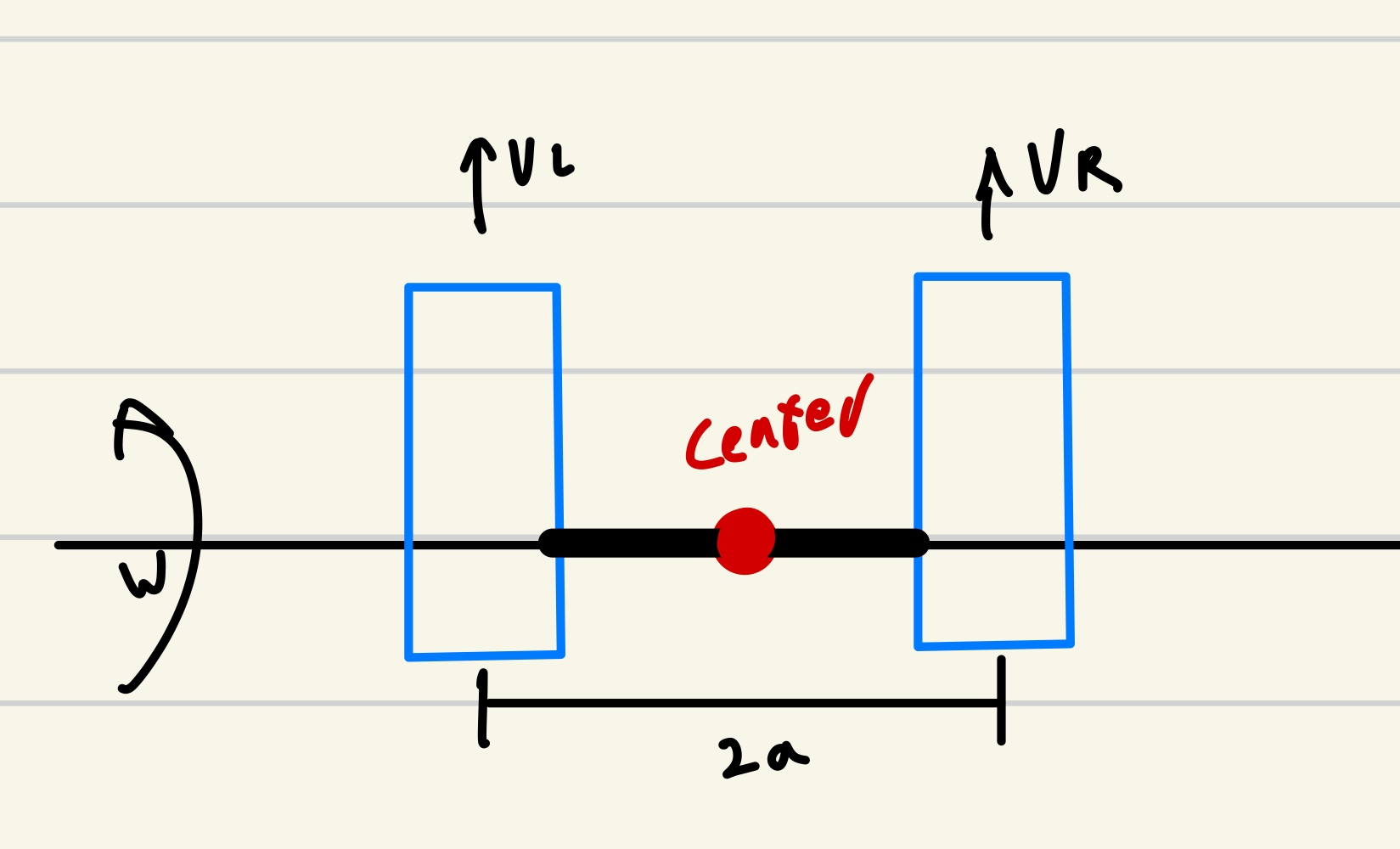
로봇의 중심을 기준으로 좌우 두개의 바퀴가 있는 가정하에 로봇이 두바퀴를 굴려 이동함
두바퀴의 선속도 같은경우 VL, VR로 정의함
결론 -> 로봇의 선속도는 두바퀴의 선속도의 평균이므로 하단 식이 도출됨
2. Rotation
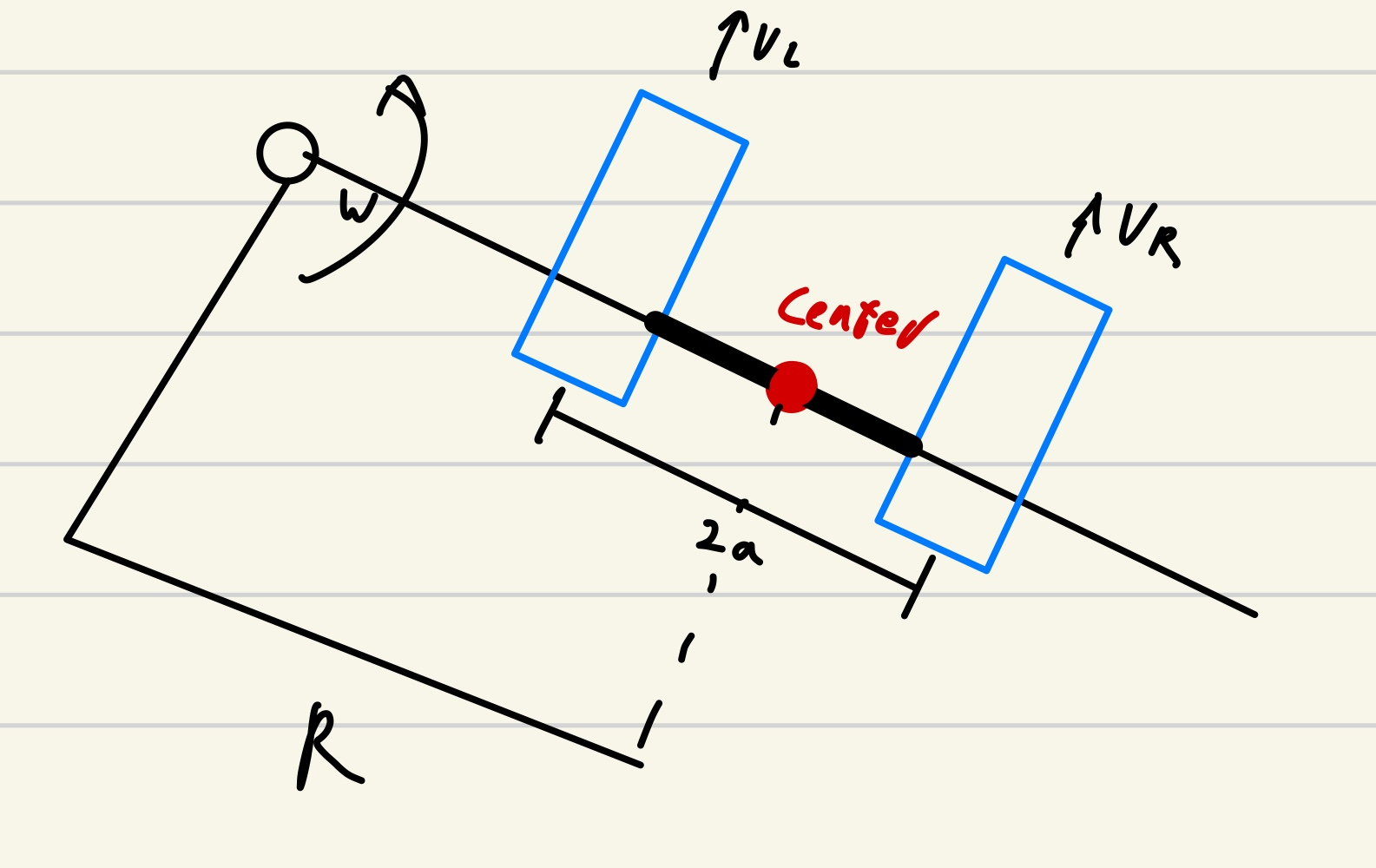
해당것은 두바퀴의 선속도를 다르게 하여 회전 운동을 진행하는데 로봇의 회전속도와 선속도의 기본공식을 작성함
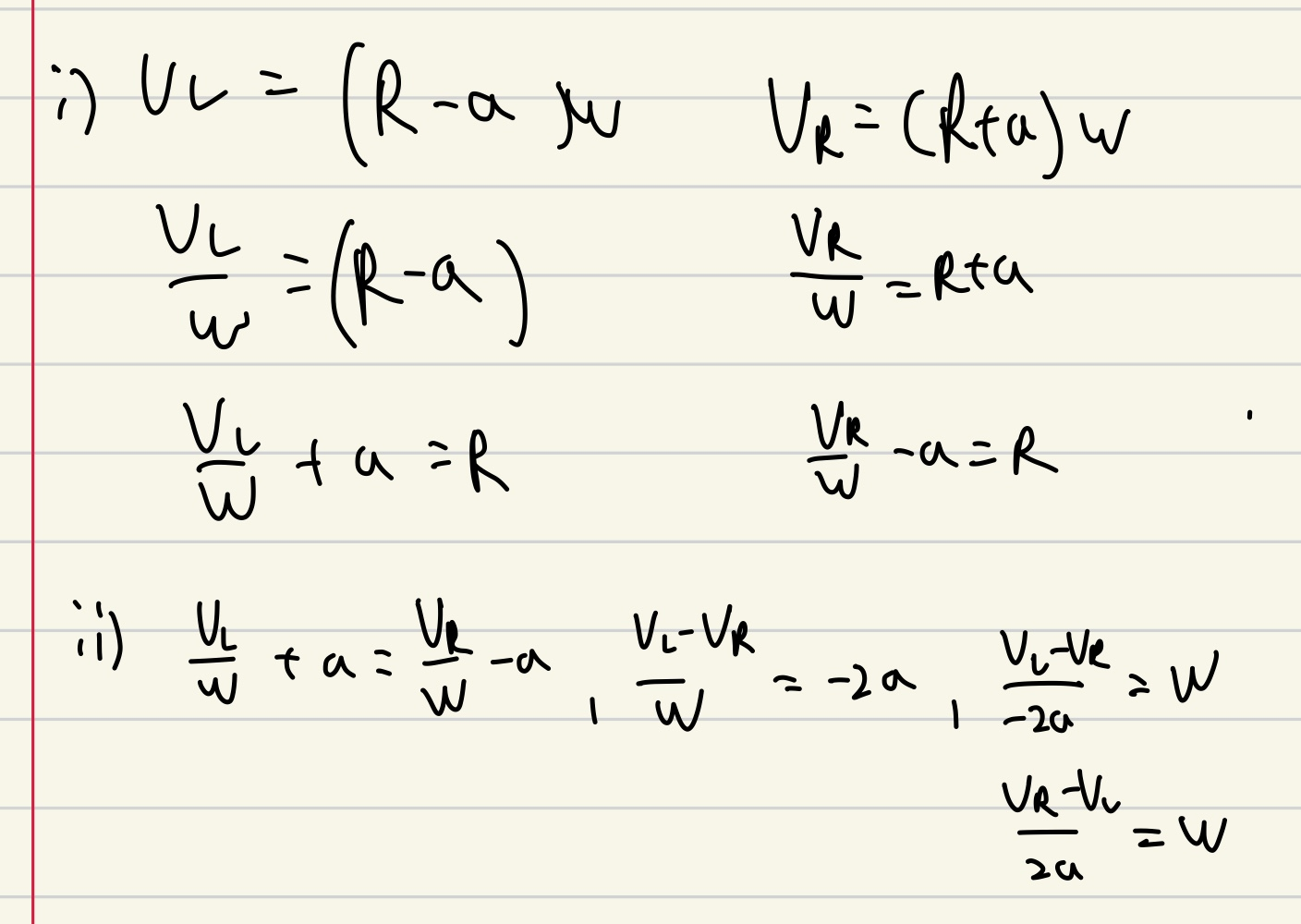
해당 V=r*w의 식을 적용하면 w의 식을 도출할수 있음
3. Differential Drive kinematics
로봇의 병진속도와 회전속도를 알아내면 두 식에 대해 세가지 케이스를 나누어 움직임을 설명할수 있음
case1 : 회전하지 않고 직진운동만 수행

case2 : 제자리 회전
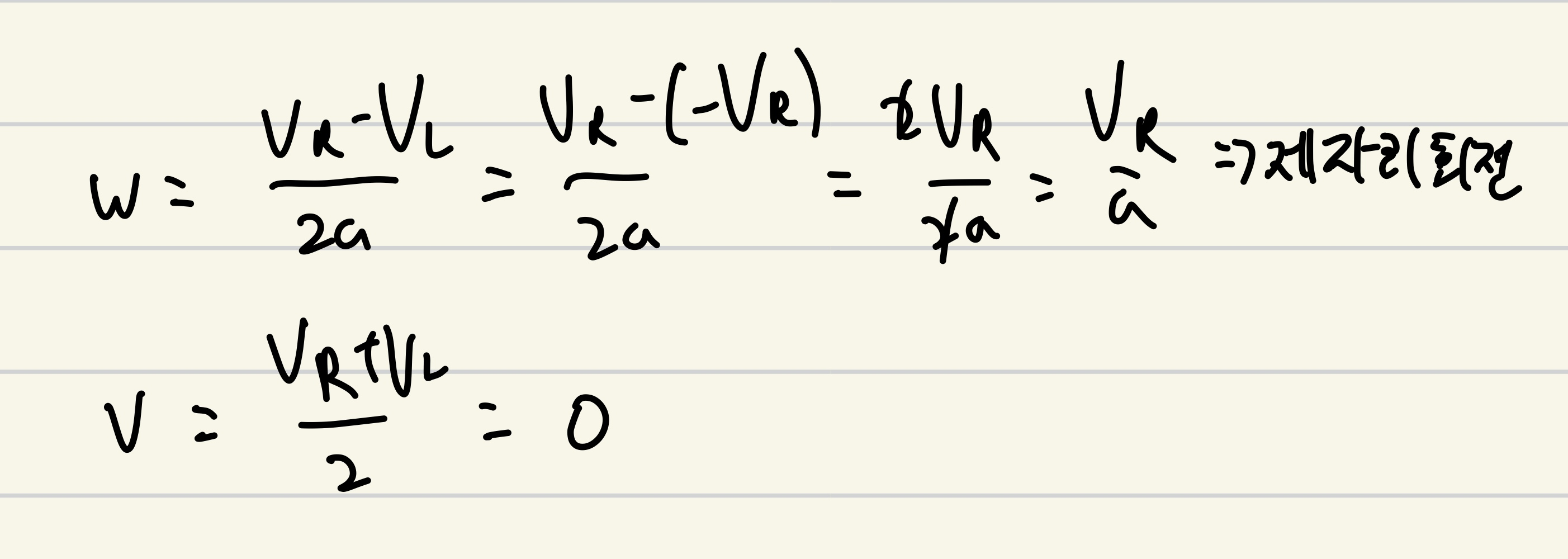
case3 : 왼쪽 바퀴를 축으로 하여 원운동
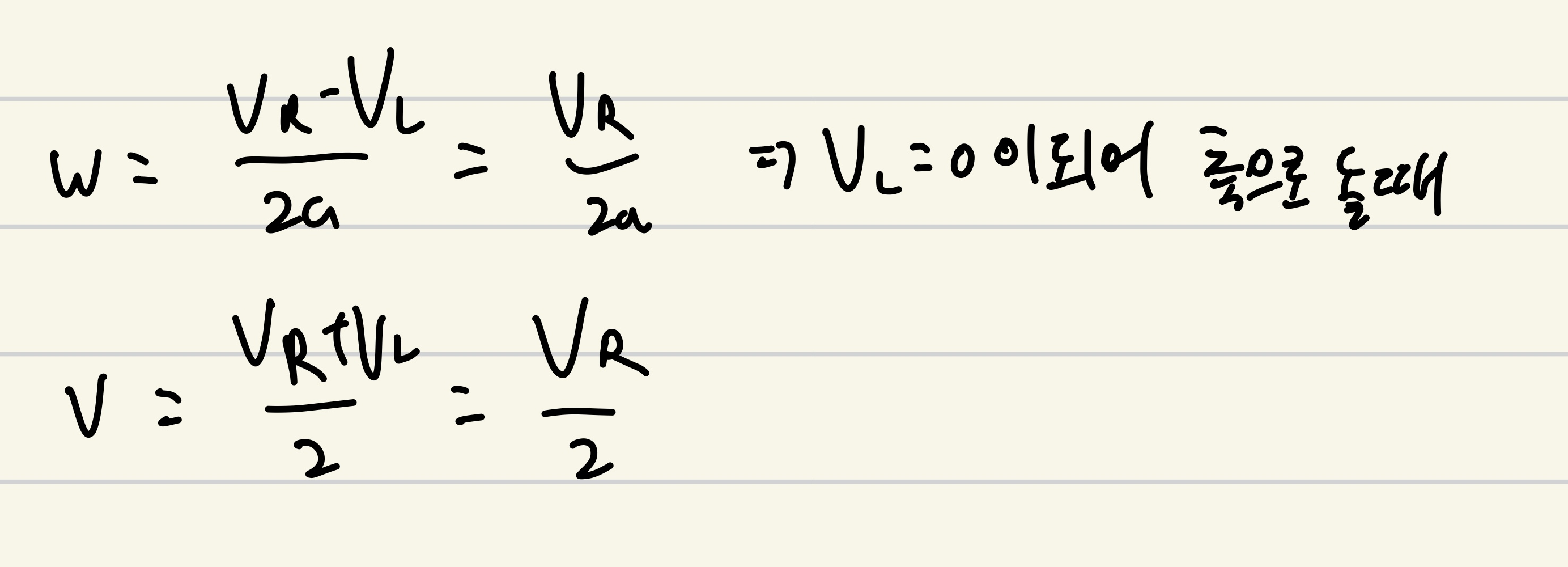
그래서 병진속도와 회전속도를 활용하여 행렬을 표현하면 이렇게 됨
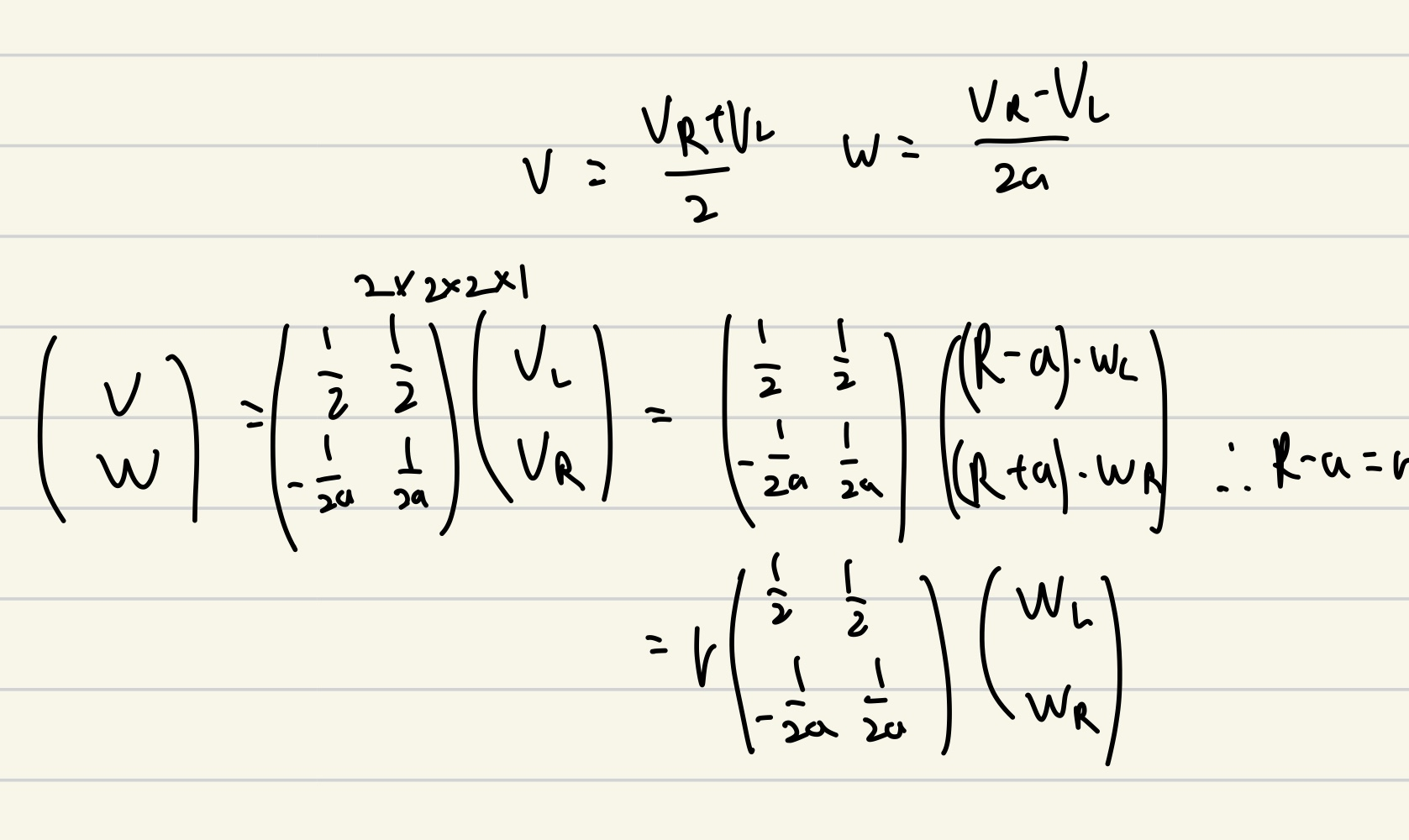
4. Jacobian(출력으로 얻은 것을 Forward kinematics)
여기서 Jacobian 이란?
자코비안 행렬은 복잡한 비선형 시스템을 최대한 선형 관계로 표현하는 수학적 도구입니다.
ex) 로봇의 각 관절 속도를 알고 있다면, 자코비안 행렬을 통해 Robot-End-Effector의 선속도와 각속도를 선형적으로 연결할 수 있습니다.
즉, 자코비안은 “조인트 속도의 변화가 말단의 위치나 자세에 어떤 영향을 미치는가”를 나타내므로, 이를 이용하면 말단의 움직임을 예측하거나 제어할 수 있음
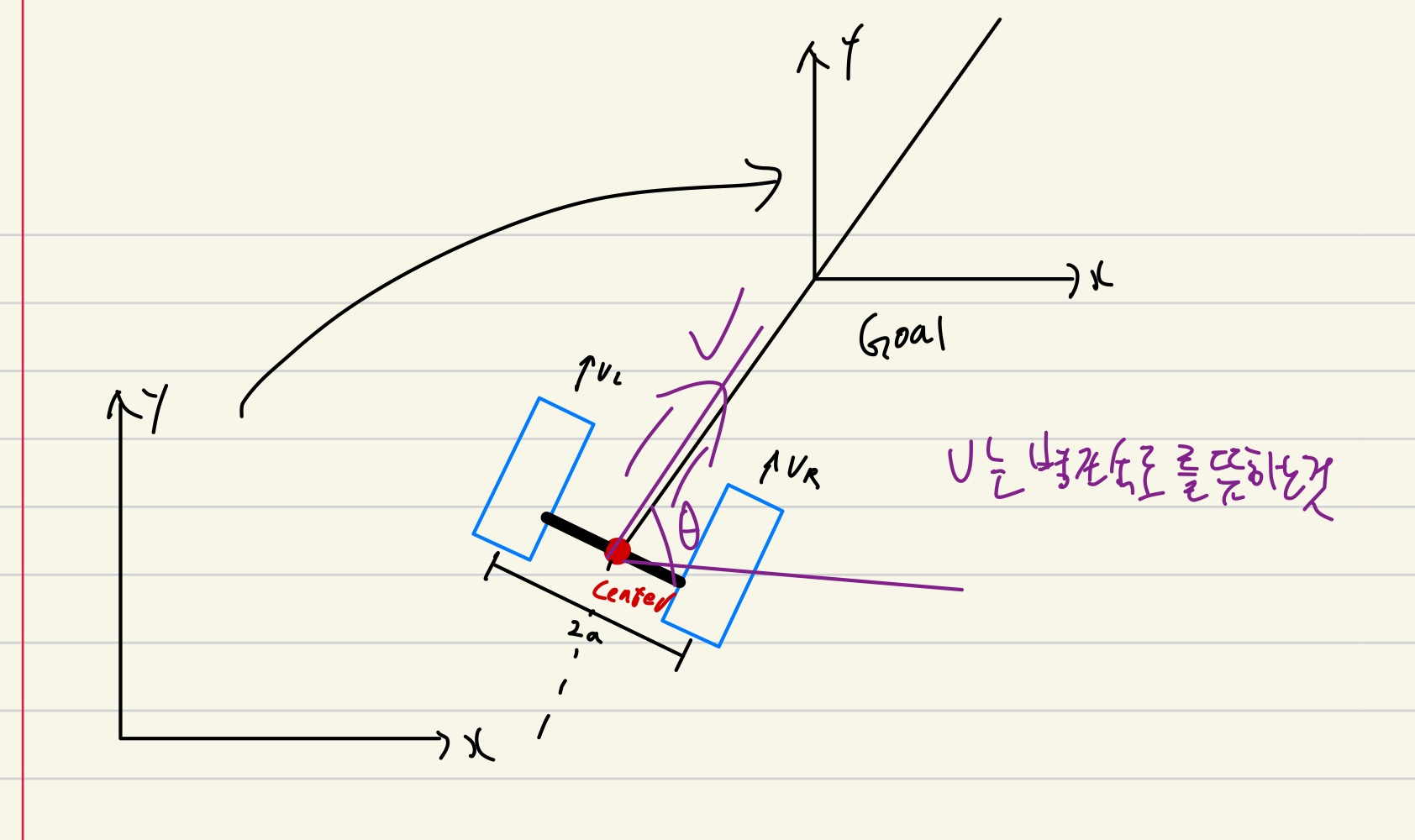
해당것에서 좌표계에 대한 구성을 로봇의 속도에 맞게 X축과 Y축을 분해하여 표현하면
그래서 해당것은 로봇의 pose를 월드좌표계로 제작할수 있는데 현재 로봇의 위치와 회전각도로 정의할수 있음
해당 것은 아래 위치 속도 가속도의 관계 덕분에 이렇게 변화가 가능하다


해당것으로 두바퀴의 각속도를입력으로 하여 로봇의 속도와 각속도 성분으로 한번의 행렬의 곱을 통해 정의됨
5. Inverse Kinematics
이는 로봇의 pose의 입력을 넣으면 로봇이 목표 pose 값으로 도달할수 있도록 합니다
자코비안 행렬은 3 X 2 행렬로 역행렬이 존재하지 않으니 이를 다른 방식으로 진행해야합니다.
x, y, 세타로 3가지의 값과 회전속도 좌측과 우측의 회전값으로 역행렬이 존재 못함
RTR Method
- 해당 방법은 움직임을 최소단위로 나누어 실행하는 것
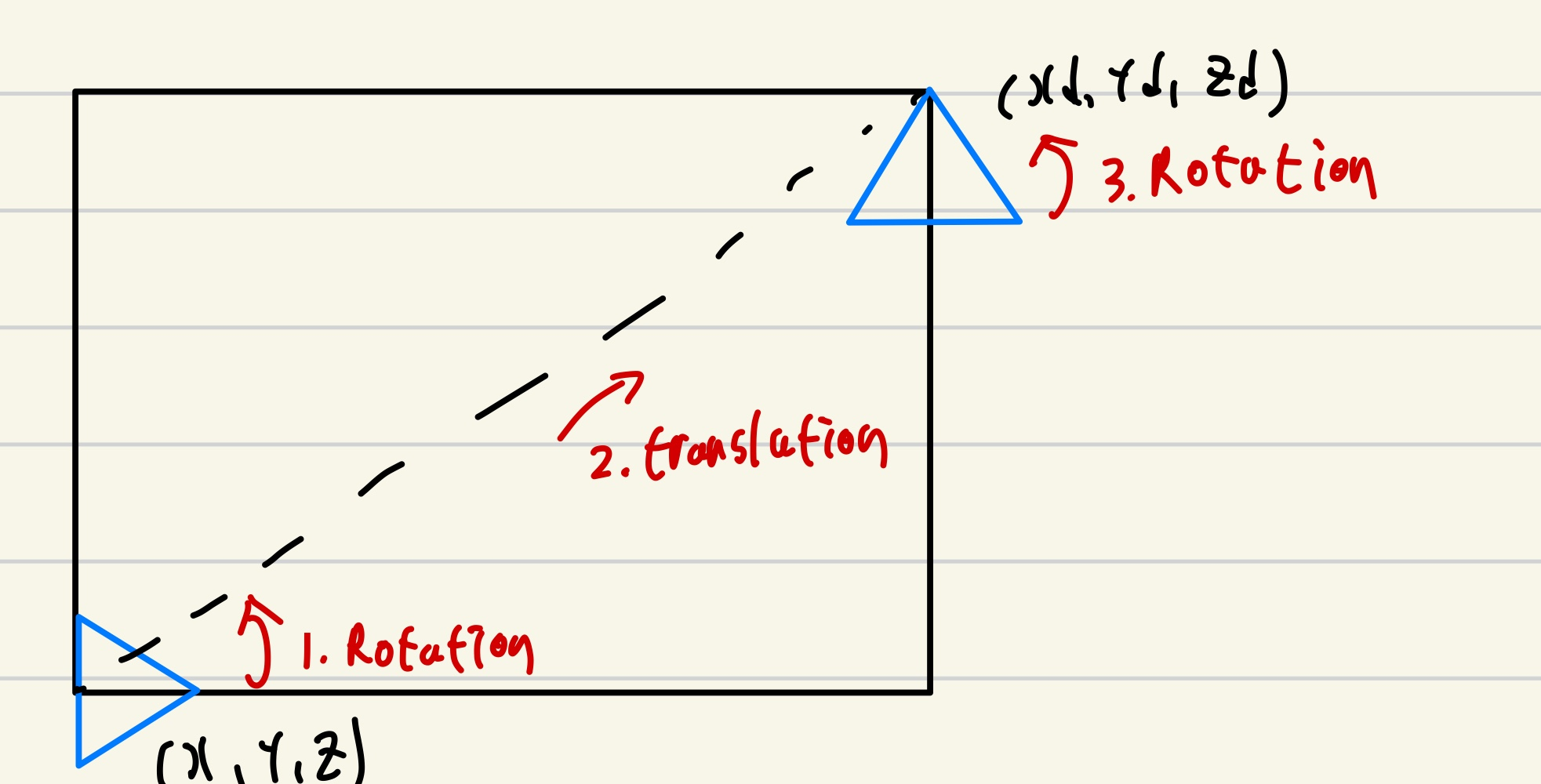
- 해당 그림과 같이 회전, 이동, 회전과 같이 분리된 움직임을 수행하는 방식이 있음
회전하는 경우 WL = (-)WR -> WR = Wo & WL = (-)Wo
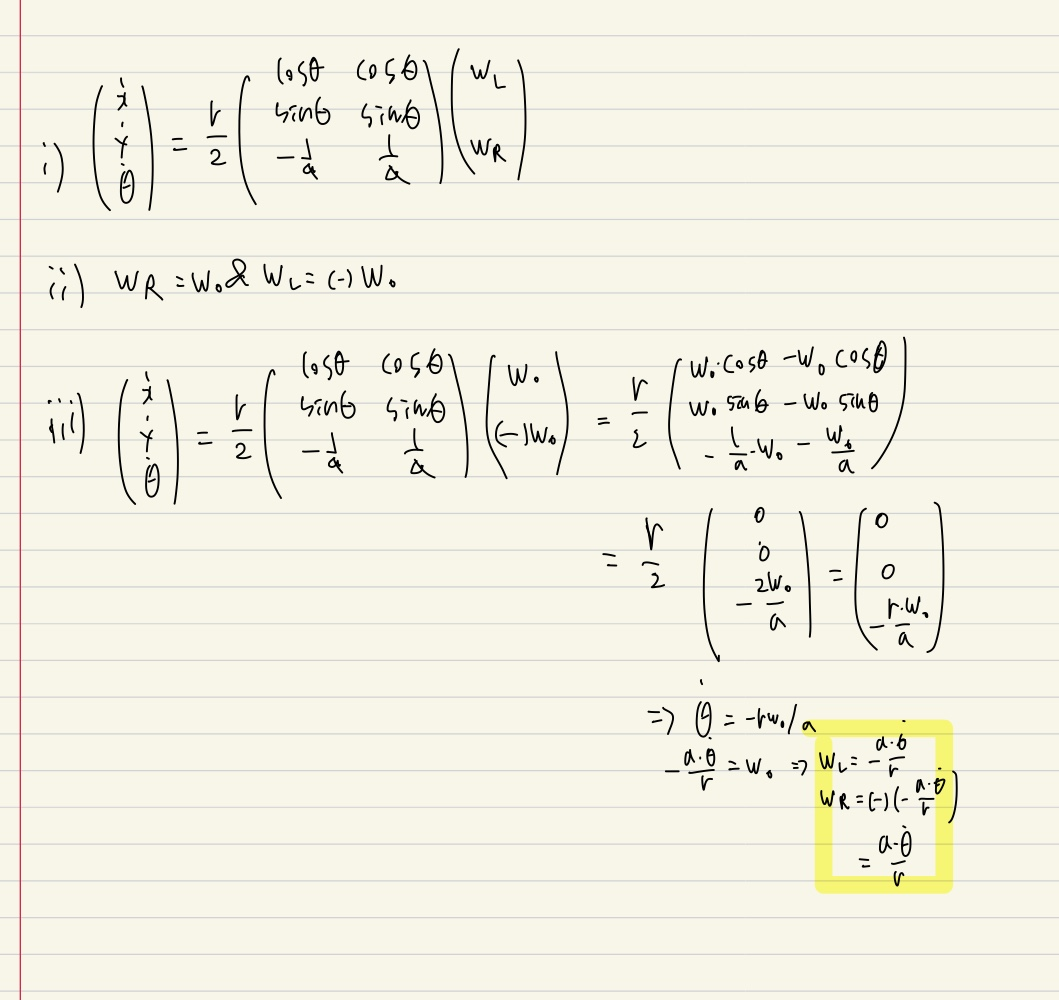
직진하는 경우 WL = WR = Wo
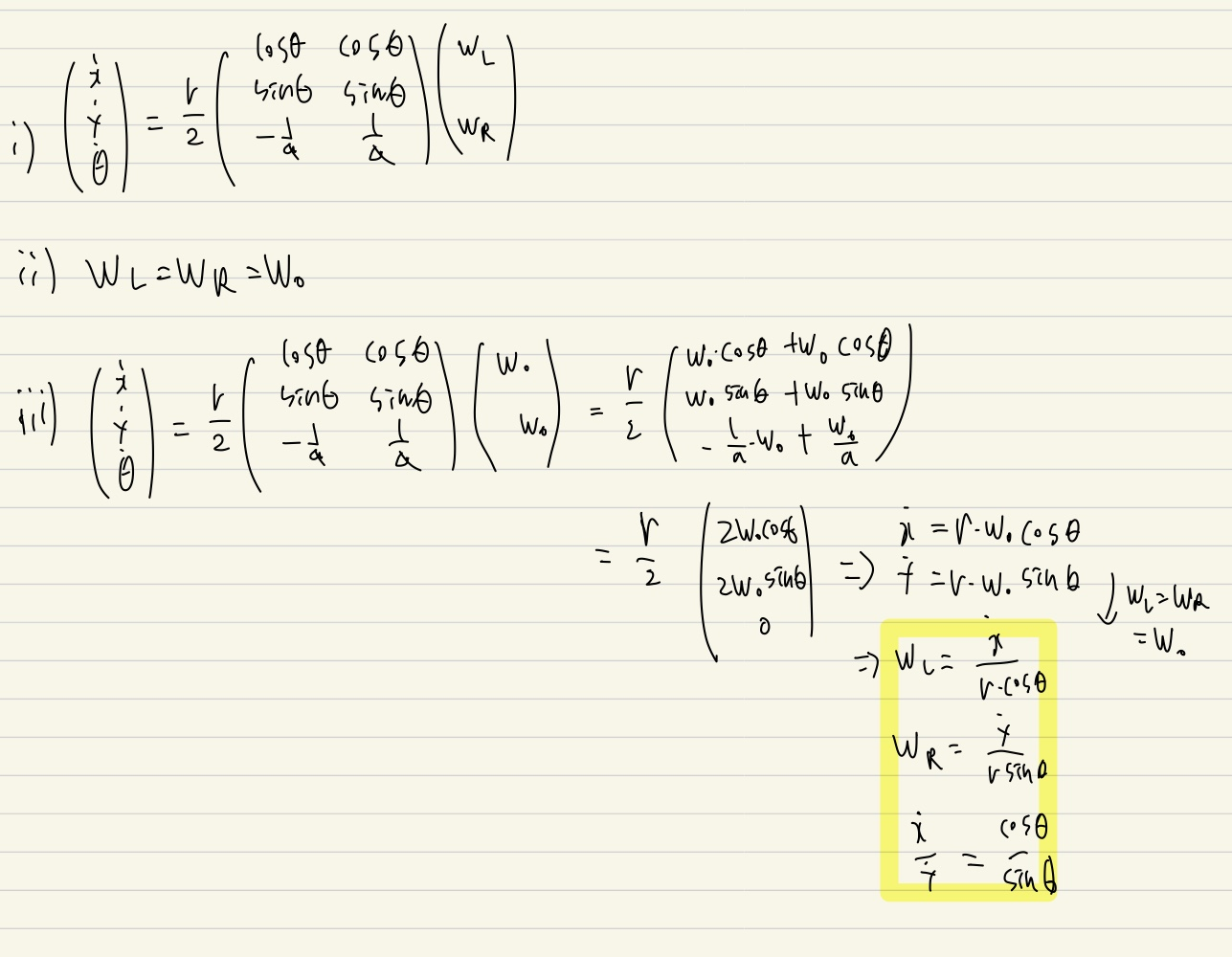
- 한계
모델링 복잡 (M, C, G 행렬 필요)
센서 노이즈, 파라미터 불확실성에 민감
자율주행 로봇처럼 “속도 제어 기반 시스템”에는 과
Inverse Kinematics with optimality
- 해당것은 로봇의 실제 자유도는 3차원이지만 독립 제어 입력 같은 경우 2개 Wr, Wl 뿐임
- 해당것 때문에 역행렬이 불가하여 차원 축소가 필요
- 비홀로노믹 제약을 이용함 -> 해당 것은 옆으로 못움직여 실직적인 제어가 가능한 차원인 2차원으로 줄임
ex) 미분 된 Y = tan(θ)*미분된 X
결론적으로 차원 축소를 사용하여 X와 θ로 시스템 제어가능

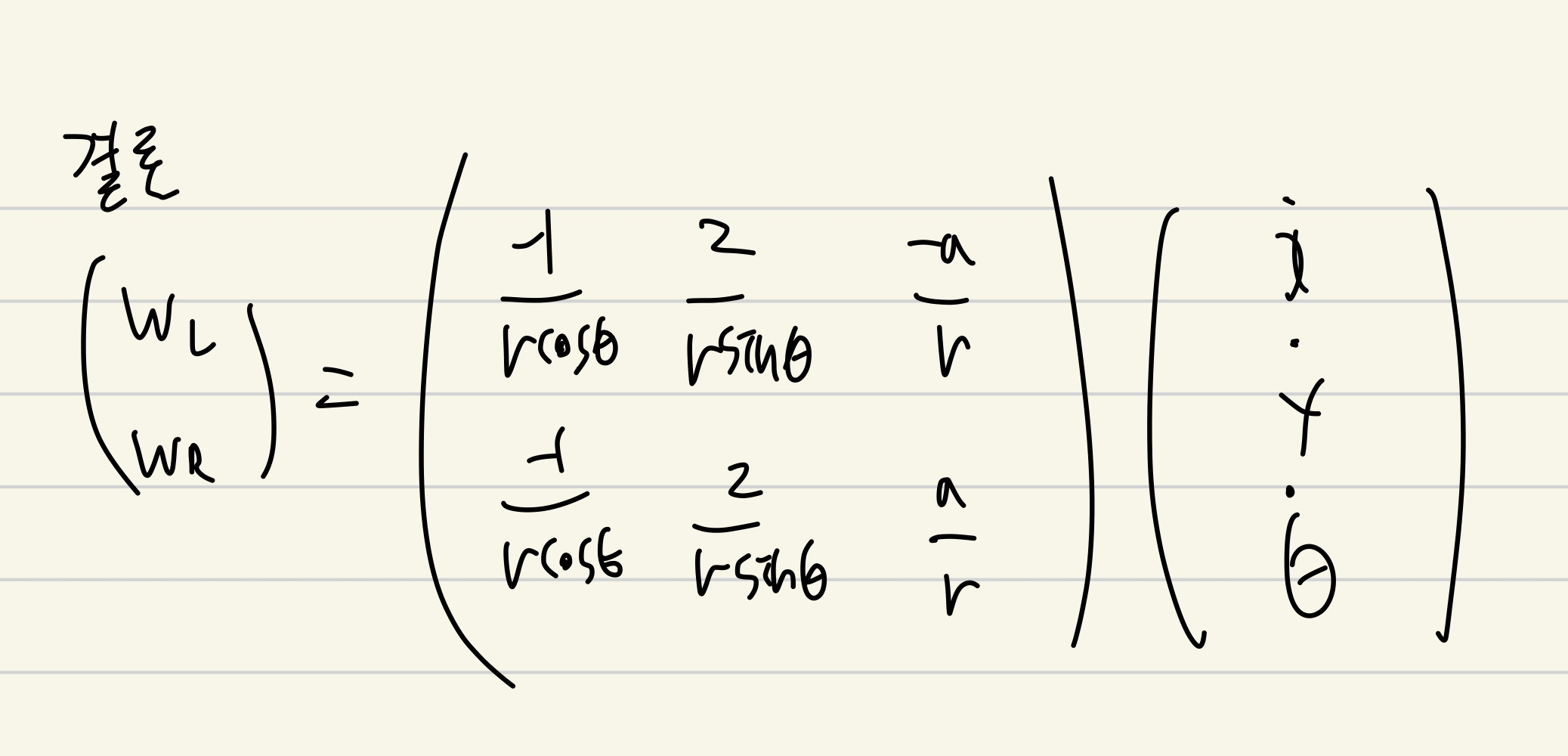
- 한계
힘, 토크, 마찰, 질량 분포 고려 X
동적 환경에서 급가속·감속 시 정확도 저하
물리 제어기 설계에는 부적합 (순수 운동학 모델만 사용)
출처
https://msjun23.github.io/mobile%20robot/mobile-robot-lec1/
https://www.youtube.com/watch?v=pY2Vppa_y38&list=PL3Ax8f2laJ6vU449FdgWlVl2VtizhDIfj
