Average Filter (평균필터)

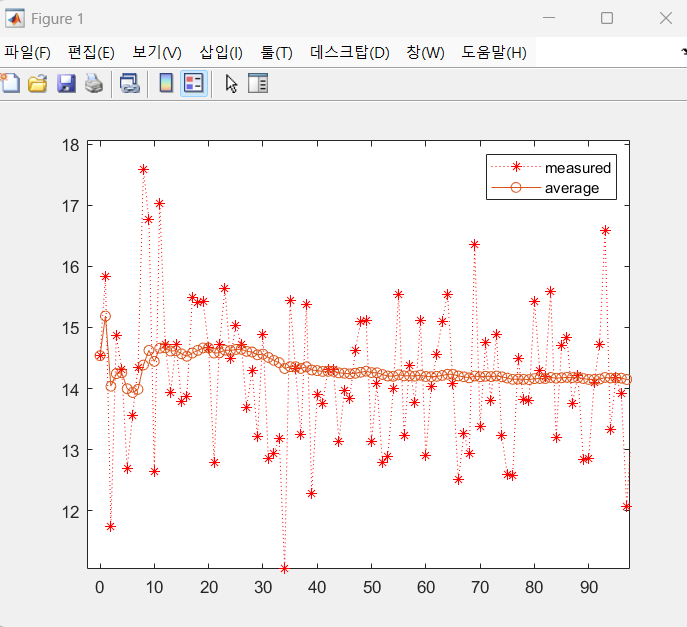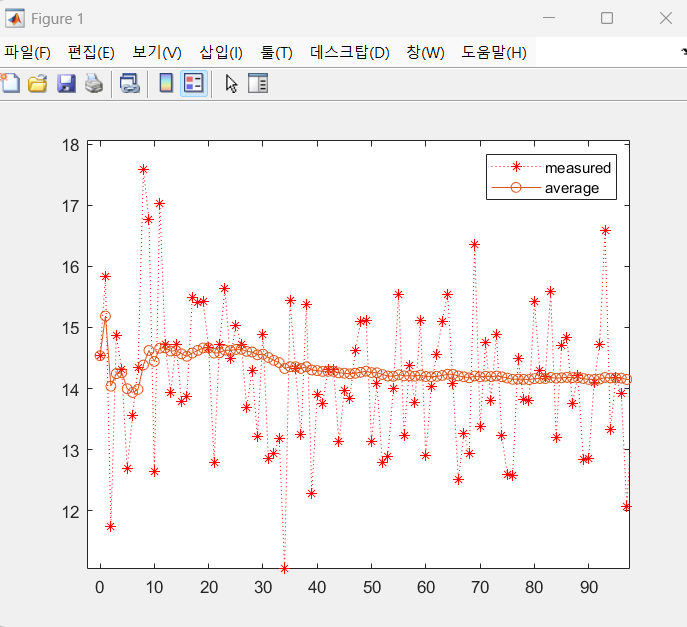
평균필터란 N개의 샘플이 있다고하면 N개를 모두 더하고 N으로 나누는 것을 의미하여 평균값을 사용하여 신호를 안정화하는 원리임 -> 가장 기본적이고 직관적인 신호처리 기법

해당 결과에서 사용한 것은

alpha = (k-1) / k

상단 공식은 평균의 가중치를 결정시킴 -> k가 늘어나면 과거데이터에 영향이 커짐

avg = alpha x preavg + (1-alpha)*x;

전에 있던 값에 가중치 값을 곱하고 나머지 가중치 값을 다음 들어오는 값에 가중치를 메김

여기서 볼수 있는 것은 가중치 값은 alpha와 1- alpha로 가중치 분배 진행

main.m

dt = 1; % 시간 간격 1초로 지정

t = 0:dt:100; %state:step:end

Nsamples = length(t); %length -> 전체 길이로 0~100까지로 101값

avgsaved = zeros(Nsamples, 1); %101*1 크기로 열 벡터를 미리 0으로 초기화

xmsaved = zeros(Nsamples, 1); %101*1 크기로 열 벡터를 미리 0으로 초기화

for k=1:Nsamples %K ~ 101까지 반복
    xm = getvolt(); %전압값을 가지고 오는 함수로 입력ㄱ밧으로 생각
    avg = avgfilter(xm); %전압값을 가지고 오는것

    avgsaved(k) = avg;
    xmsaved(k) = xm;
end

figure
plot(t, xmsaved, 'r:*')
hold on
plot(t, avgsaved, 'o-')
legend('measured', 'average')

getvolt.m

function z = getvolt()

w = 0 + randn(1,1); %평균 0 과 표준편차 1를 난수 1개 생성
z = 14+w; %약 14V로 잡음```

avgfilter.m

function avg = avgfilter(x)

persistent preavg k 

%영속변수를 만듬-> 영속변수란 함수가 여러번 호출되도 값이 유지됨
% 여기서는 preavg -> 이전평균값, k -> 입력된 데이터의 개수

persistent firstrun

if isempty(firstrun)
    k = 1;
    preavg = 0;

    firstrun = 1;

end

alpha = (k-1)/k; %평균의 가중치를 결정시킴 -> k가 늘어나면 과거데이터에 영향이 커짐

avg = alpha * preavg + (1-alpha)*x;
% alpha * preavg  : 이전 평균값의 영향을 끼침
% (1-alpha)*x

preavg  = avg;
k = k+1;

참조

https://limitsinx.tistory.com/69