[객체인식 & Depth Estimation 프로젝트] 6. Depth 추정 (Homography) + Bird-Eye view 표현

happy_quokka·2024년 1월 29일

Perception Xycar 프로젝트

자율주행 프로젝트

목록 보기

12/15

Depth 추정

object와 자이카와의 depth를 추정하여 즉, 거리를 추정하여 추후에 자이카를 제어한다
depth를 추정하는 방법에는 크게 3가지가 있는데 여기에서는 homography를 사용하는 방법을 선택했다
그 이유은 homography 방법은 간단하지만 지면이 평평한 경우에만 사용할 수 있는데 프로젝트 환경은 평평한 바닥이기 때문에 이 방법을 선택하였다

homography

간단하게 정리를 하자면 homography는 두 평면 간의 변환 관계를 의미한다
최소 4짱의 좌표값을 알면 homography matrix를 구할 수 있다

이 경우에는 바닥 평면과 카메라 이미지 평면 간의 관계를 구하는 것이다

Depth 추정 과정

1. world 좌표와 image 좌표쌍 구하기

최소 4쌍 이상의 좌표쌍이 필요한데 많을수록 정확한 homography matrix를 구할 수 있기 때문에 많은 좌표쌍을 구했다
최대한 멀리, 넓게 좌표쌍을 정해야 정확한 값을 얻을 수 있다

바닥 평면의 원하는 지점에 블록을 놓고 이미지를 촬영한다
이렇게 하는 이유는 바닥 평면의 grid 선이 이미지 상에서 뚜렷하게 보이지 않기 때문에 원하는 좌표쌍을 얻기 위해 잘 보이는 블록을 놓아서 이미지를 획득하였다
이때 자이카를 원하는 지점에 놓고 그 지점부터 블록까지의 거리를 알고 있어야한다
이 경우에서는 자이카의 가장 앞 부분을 (270, 540) 좌표에 맞춰서 놓고 이미지를 획득하였다

바닥 평면의 한 grid의 실제 크기는 45cm이다
하지만 조금 더 넓은 평면으로 변환을 하고 싶었기 때문에 90으로 조정하였다
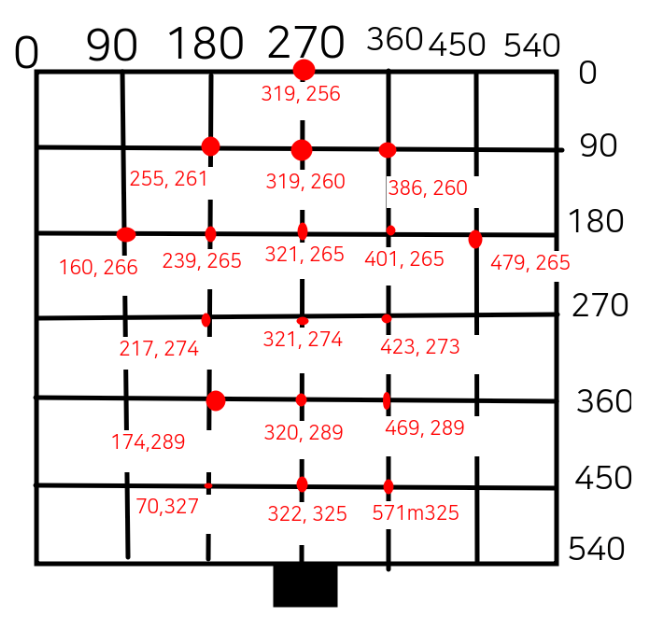
아래 오른쪽 이미지를 보면 검은색 grid는 바닥 평면을 의미하고 빨간색 좌표는 카메라에서 획득한 이미지 상에서의 좌표를 의미한다

world 좌표는 (x, y, 1) 과 같이 homography 좌표로 표현해야하고, image 좌표는 (x, y) 로 표현해야한다

# x, y, 1
homo_3d_points = numpy.array([
    [270, 0, 1],
    [180, 90, 1],
    [270, 90, 1],
    [360, 90, 1],
    [180, 180, 1],
    [270, 180, 1],
    [360, 180, 1],
    [180, 270, 1],
    [270, 270, 1],
    [360, 270, 1],
    [180, 360, 1],
    [270, 360, 1],
    [360, 360, 1],
    [180, 450, 1],
    [270, 450, 1],
    [360, 450, 1],
    [90,180, 1],
    [450,180, 1]
], dtype=numpy.float32)

# x, y
homo_points = numpy.array([
    [319, 256],
    [255, 260],
    [319,260],
    [386,260],
    [241, 265],
    [321, 265],
    [401,265],
    [217, 274],
    [321, 274],
    [423, 273],
    [174, 289],
    [320,289],
    [469,289],
    [70,327],
    [322,325],
    [571,325],
    [160,265],
    [479,265]
], dtype=numpy.float32)

2. homography matrix 구하기

opencv의 findHomography 함수를 사용하여 계산한다
이때 method 옵션으로 RANSAC을 사용하면 outlier로 인한 오차를 줄여줄 수 있다고 한다

homography, _ = cv2.findHomography(homo_points, homo_3d_points, method=cv2.RANSAC)

## homography matrix
[[-1.36650485e-01, -1.13733437e+00, 3.12113770e+02],
 [ 6.53381187e-04, -2.45035619e+00, 6.27102327e+02],
 [ 3.93808370e-06, -4.24034141e-03, 1.00000000e+00]]

3. depth 구하기

3-1. 원하는 object의 좌표 구하기

예측한 object의 bounding box에서의 밑변의 중심 좌표를 구한다
밑변으로 해야하는 이유는 object가 바닥과 붙어있는 지점으로 해야지 거리를 구할 수 있기 때문이다
여기에서 x0, x1은 bounding box의 min_x, max_x를 의미한다
y0, y1은 bounding box의 min_y, max_y를 의미한다

x0 = int(box[0])
y0 = int(box[1])
x1 = int(box[2])
y1 = int(box[3])

center_x = (x0 + x1)/2

3-2. image 좌표를 world 좌표로 변환하기

앞에서 구한 homography matrix를 사용하면 image 좌표값을 world 좌표값으로 변환할 수 있다
image 좌표값을 homography 좌표로 변환하고 내적을 수행하면 x, y, z값이 나온다
이때 z값은 1이여야하기 때문에 x, y, z를 z로 나누면 원하는 world 좌표상의 x, y 값을 구할 수 있다

bbox_point = np.array([center_x, box[3], 1])
estimate = np.dot(self.homo_mat, bbox_point)
x, y, z = estimate[0], estimate[1], estimate[2]

depth_x = x/z
depth_y = y/z

3-2. depth 계산하기

depth는 자이카와 원하는 object와의 거리를 의미한다
자이카가 (270,540) 좌표에 위치해 있기 때문에 이 좌표와의 거리를 계산하면 된다
방법 1은 두 점 간의 거리를 계산한 것으로 x, y 좌표를 모두 고려한 것이다. 프로젝트 때는 이 방법을 사용하였다
방법 2은 y 좌표만 고려한 것이다

# 방법 1
distance = int(np.sqrt(((270 - depth_x)/2)**2 + ((540-depth_y)/2)**2))

# 방법 2
distance = int((540 - depth_y)/2)

Bird-Eye View (BEV) 표현

Bird-Eye view는 위에서 바라본 것을 의미한다
자이카와 그 주변의 object들이 어떻에 위치해있는지 보기 위해 Bird-Eye view로 그 좌표값들을 변환하였다

방법 1의 경우 카메라 이미지를 BEV로 변환한 것이다
하지만 이 결과는 깔끔해보이지 않기 때문에 방법 2를 선택하였다
방법 2의 경우 그냥 검은 이미지를 의미하고 추후에 world 좌표로 표현한 object의 위치를 여기에 나타내 주었다

# 방법 1
bev_img = cv2.warpPerspective(bev_img, self.homo_mat, (540,540))

# 방법 2
bev_img = np.zeros((540, 540, 3), dtype=np.uint8)

# 시각화 
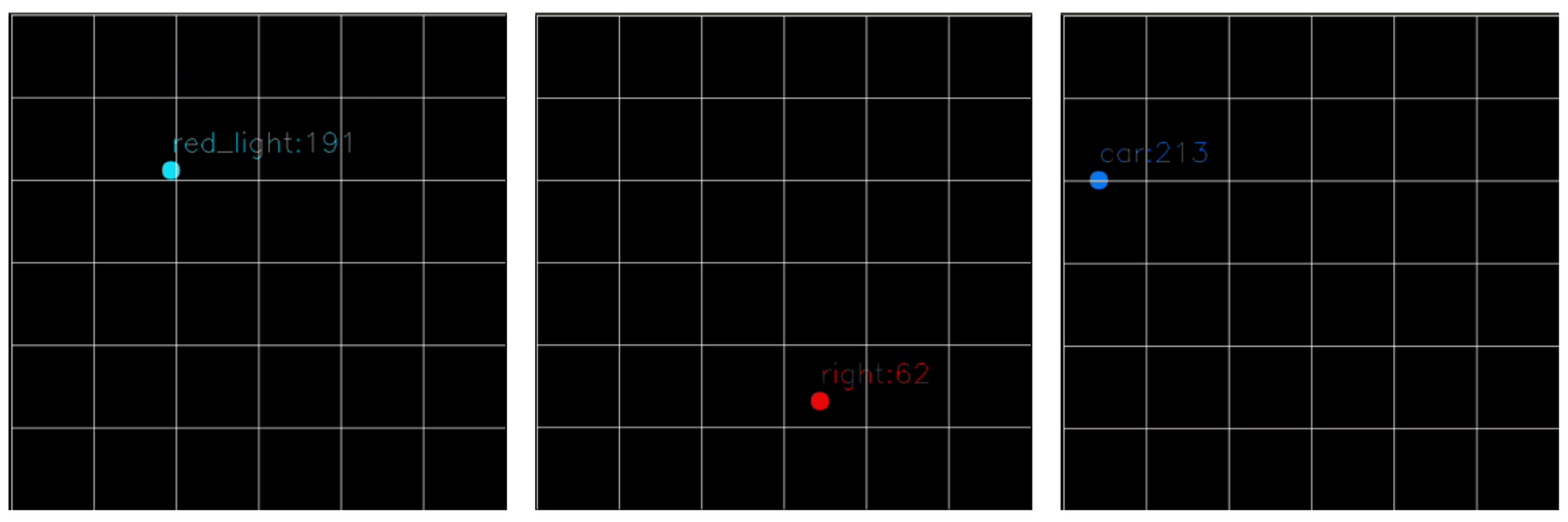
depth_text = '{}:{}'.format(class_names[cls_id], distance)
cv2.circle(bev_img, (int(depth_x), int(depth_y)), 10, color, -1)
cv2.putText(bev_img, depth_text, (int(depth_x), int(depth_y) - 20), font, 1, color, thickness=1)