7. 스케일링
- 데이터의 범위를 조정하는 과정
- 다양한 특성들이 서로 다른 범위와 단계를 가질 때 이를 일관된 범위로 조정하여 모델이 효율적으로 학습할 수 있도록 함
7.1 Scikit-Learn
7.1.1 Scikit-Learn
- python을 대표하는 머신러닝 라이브러리
- 매우 다양한 전처리 도구와 알고리즘을 제공
- 머신러닝 학습에 적합
- 분류, 회귀, 클러스터링, 차원 축소 등을 포함한 광범위한 머신러닝 알고리즘을 제공
- 데이터의 전처리에 적합
- 데이터 변환, 정규화, 스케일링, 결측치 처리 등과 같은 여러 데이터 전처리 기능을 제공
- 예제와 사용 설명서가 잘 되어있어 참고하여 코드를 작성하기 용이
- 머신러닝 학습에 적합
- 데이터 분석을 위한 간단하고 효율적인 도구 제공
- 간단하고 직관적인 API를 제공하므로 다양한 수준의 전문 지식을 가진 사용자가 접근 가능
- fit(), transform(), predict() 등 체계적이고 일관된 분석 및 학습모형 운용 체계를 갖추고 있음
- 다른 많은 패키지도 scikit-learn과 동일한 체계를 제공하여 유사한 프레임에서 사용이 가능
- 간단하고 직관적인 API를 제공하므로 다양한 수준의 전문 지식을 가진 사용자가 접근 가능
- 다른 파이썬 패키지와 함께 사용하기 용이
- NumPy, Pandas, SciPy 및 matplotlib를 기반으로 구축되어 있음
- NumPy: 다차원 배열을 위한 기본 패키지
- Pandas: 데이터프레임을 위한 기본 패키지
- SciPy: 과학 계산용 함수를 모아놓은 패키지
- matplotlib: 데이터 시각화를 위한 패키지
- NumPy, Pandas, SciPy 및 matplotlib를 기반으로 구축되어 있음
- 단점
- 딥러닝, 강화학습, 시계열 모형은 매우 약함
- TensorFlow, PyTorch 과 같은 다른 라이브러리가 더 적합하다.
- 최근 개발된 대용량을 위한 데이터프레임인 Polars와 같은 라이브러리와는 연동이 잘 안됨
- 딥러닝, 강화학습, 시계열 모형은 매우 약함
7.1.2 Scikit-Learn의 주요 기능
- 분류: 로지스틱 회귀, 결정 트리, 서포트 벡터 머신(SVM)
- 회귀: 선형 회귀, 릿지 회귀 등
- 군집화: k-평균 군집화, 계층적 군집화 등
- 차원 축소: 주성분 분석(PCA), t-분산 확률적 이웃 내재화(t-SNE) 등
- 전처리: 데이터 정규화, 스케일링, 인코딩 등
7.2 Scikit-Learn Preprocessing
Scikit-learn의 전처리 기능은 크게 4가지로 나눌 수 있음
- 스케일링(scaling): 서로 다른 변수의 값 범위를 일정한 수준으로 맞추는 것
- 이진화(binarization): 연속적인 값을 0 또는 1로 나누는 것, 연속형 변수 → 이진형 변수
- 인코딩(encodig): 범주형 값을 적절한 숫자형으로 변환하는 작업, 범주형 변수 → 수치형 변수
- 변환(transformation): 데이터의 분포를 변환하여 정규성을 확보하는 것
- 모델 성능개선 및 안정적 데이터 분석 결과를 위해
7.2.1 Scaling
- 서로 다른 변수(feature)의 값 범위를 선형변환을 통하여 일정한 수준으로 맞추는 작업
- 독립변수(feature)별로 값의 변위가 상이하면
- 종속변수(target)에 대한 영향이 독립변수의 변위에 따라 크게 달라짐 → 머신러닝 시 학습효과가 떨어짐
- 다차원의 값들을 동일한 수준에서 비교 분석하기 용이하게 만들어 줌
- 컴퓨터의 비트수로 인하여 다른 값으로 인식되는 오버플로우(overflow)나 언더플로우(underflow)를 방지
- 최적화 과정에서의 안정성 및 수렴 속도를 향상
- 특히 k-means 등 거리 기반의 모델에서는 스케일링이 매우 중요
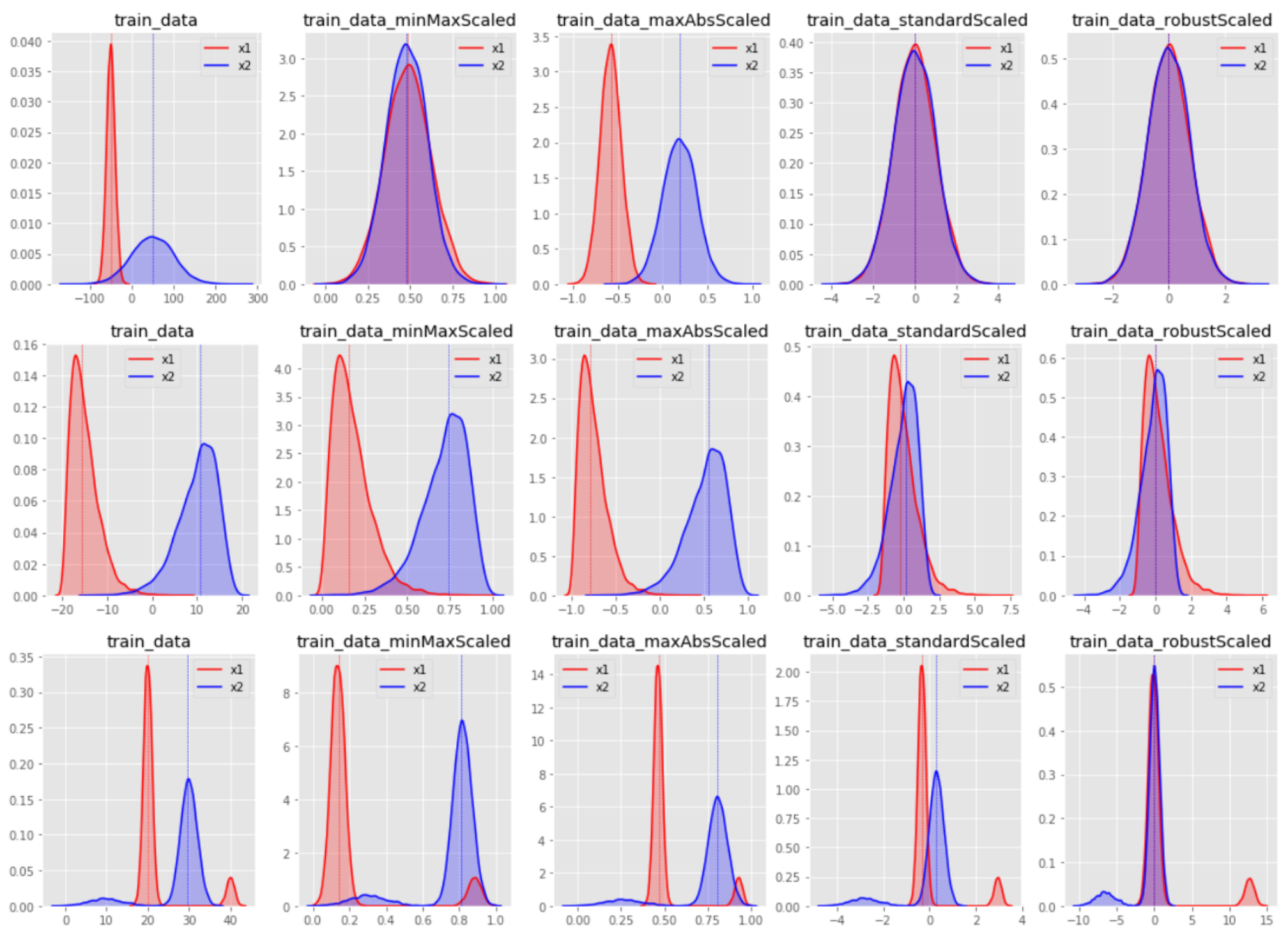
- 독립변수(feature)별로 값의 변위가 상이하면
7.2.2 Scaling 의 절차
Scaler 객체를 이용한다
- fit(): 주어진 데이터에 맞추어 학습
- 데이터 변환을 위한 기준 정보 설정을 적용 (ex.최소값,최대값 등)
- transform(): Scaler 적용, fit()된 정보를 이용해 데이터를 변환
- fit_transform() : fit()과 transform()을 한 번에 실행
훈련 데이터와 평가 데이터의 스케일링 변환 시 유의점
- 훈련 데이터는 fit()과 transform() 모두 적용
- 평가 데이터는 fit()은 필요없으므로 transform()만 적용해야 함
- 훈련 데이터로 fit()된 스케일링 기준 정보를 그대로 테스트에 적용해야하기 때문
1. 표준화(Standardization)
- 표준분포화(평균을 0, 분산을 1 로 스케일링)
- 데이터의 특성들이 서로 다른 스케일을 가질 때 유용
- StandardScaler(): 기본 스케일러, 평균과 표준편차 사용
* 데이터를 정규 분포로 만들어준다.
- RobustScaler(): 중앙값과 IQR(Q3-Q1)을 사용. 이상치의 영향을 최소화
2. 정규화(Normalization) → 규격화(특정 범위(주로 [0,1]) 로 스케일링)
- 차원 데이터를 처리할 때 각 특성의 범위를 동일하게 만들어 비교하기 쉬워짐
- MinMaxScaler(): 범위가 [0,1]이 되도록 스케일링
- 데이터의 최소값과 최대값에 대해 민감하다.
- MaxAbsScaler(): 양수는 [0,1], 음수는 [-1,0], 양음수는 [-1,1]이 되도록 스케일링
3. 변환(Transformation) (특정한 분포나 모양을 따르도록 스케일링)
- 데이터의 분포가 특정 분포(예: 정규 분포)를 따르도록 하거나, 각 특성들 사이의 관계를 보다 명확하게 표현하기 위해 사용
- PowerTransformer(): 정규분포화(Box-Cox 변환, Yeo-Johnson 변환)
- QuantileTransformer(): 균일(Uniform)분포 또는 정규(Gaussian)분포로 변환
- Normalizer(): 한 행의 모든 피처들 사이의 유클리드 거리가 1이 되도록 변환
7.3 표준화 (Standardization)
표준화의 중요성 및 특성
-
서로 다른 통계 데이터들을 비교하기 용이함
- 평균은 0, 분산과 표준편차는 1이 되므로 데이터의 분포가 단순화되어 독립변수간 데이터 - 수준의 비교가 용이
-
알고리즘의 성능향상에 도움
- RBF(Radial Basis Function) 커널을 이용하는 서포트 벡터 머신(Support Vector - Machine), 선형회귀(Linear Regression), 로지스틱 회귀(Logistic Regression)는 데이터가 정규분포를 가지고 있다고 가정하고 구현됨
- RBF Kernel: Gaussian kernel, 가우시안 방사 기저 함수
- RBF(Radial Basis Function) 커널을 이용하는 서포트 벡터 머신(Support Vector - Machine), 선형회귀(Linear Regression), 로지스틱 회귀(Logistic Regression)는 데이터가 정규분포를 가지고 있다고 가정하고 구현됨
-
이상치에 민감함
- 이상치가 존재하는 경우 데이터의 평균과 표준편차가 왜곡될 수 있으므로
-
분류보다는 회귀에 유용함
- 회귀분석은 변수 간 관계를 설명하는데 사용 되며, 표준화된 변수는 관계 설명에 도움이 됨
기저함수와 커널
(1) 기저함수
- 기저함수(basis function, ϕ) 혹은 feature map 이라고 함
- 원래의 데이터 공간(입력 공간)의 데이터를 더 높은 차원의 특징 공간(특성 공간)으로 변환하는 함수
- 비선형 특징을 가지는 Input space를 선형 특징을 가지는 Feature space로 변환해주는 함수
- 작동원리: 데이터의 각 차원을 변환하여 새로운 특징을 생성
- 예를 들어, 2차원 데이터를 3차원 혹은 그 이상의 차원으로 변환
- 비선형 문제를 해결할 때 유용함
(2) 커널
- 알맹이, 핵심이라는 뜻
- 운영체제 및 수학에서의 의미 및 활용
- 운영체제(Operation System)에서는 컴퓨터 자원을 관리하는 핵심 부분을 의미
- 수학에서는 기저함수의 내적을 계산하는 함수
- 커널함수는 두 벡터를 입력받아서 하나의 스칼라 값을 계산하는 함수
- 일종의 변환함수라고 생각하면 됨
- 데이터 사이언스분야에서...
- 두 벡터(데이터 포인트) 간의 유사도를 측정하는 함수
- 고차원 공간에서의 복잡한 계산을 간소화하여, 비선형 문제를 효율적으로 해결
- 많이 사용되는 커널
- 선형 서포트 벡터 머신
- 다항 커널 (Polynomial Kernal)
- RBF(Radial Basis Function) 또는 가우시안 커널(Gaussian Kernal)
- 시그모이드 커널
7.4 정규화 (Normalization)
-MinMaxScaler(): 범위가 [0,1]이 되도록 스케일링
-MaxAbsScaler()
- 모든 값이 양수이면, 범위가 [0,1]이 되도록 스케일링, MinMaxScaler()와 유사
- 모든 값이 음수이면, 범위가 [-1,0]이 되도록 스케일링
- 양수와 음수가 혼재하면, 범위가 [-1,1]이 되도록 스케일링
7.5 변환 (Transformation)
- PowerTransformer(): 정규성 변환(Box-Cox 변환, Yeo-Johnson 변환)
- QuantileTransformer(): 균일(Uniform)분포 또는 정규(Gaussian)분포로 변환
- Normalizer(): 한 행의 모든 피처들 사이의 유클리드 거리가 1이 되도록 변환
7.6 응용: Diabetes 데이터 활용하여 스케일링
STEP 1. 데이터 불러오기
import pandas as pd
from sklearn.datasets import load_diabetes
# 당뇨병 데이터셋 불러오기
diabetes = load_diabetes()
# 데이터를 DataFrame으로 변환하고 컬럼 이름 지정
diabetes = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
# 데이터셋의 처음 몇 개 행 출력
print(diabetes.head())

# 기술통계량을 확인
diabetes.describe()
# bmi와 bp의 jointplot을 그림
sns.jointplot(data=diabetes, x='bmi', y='bp', kind='scatter')
plt.show()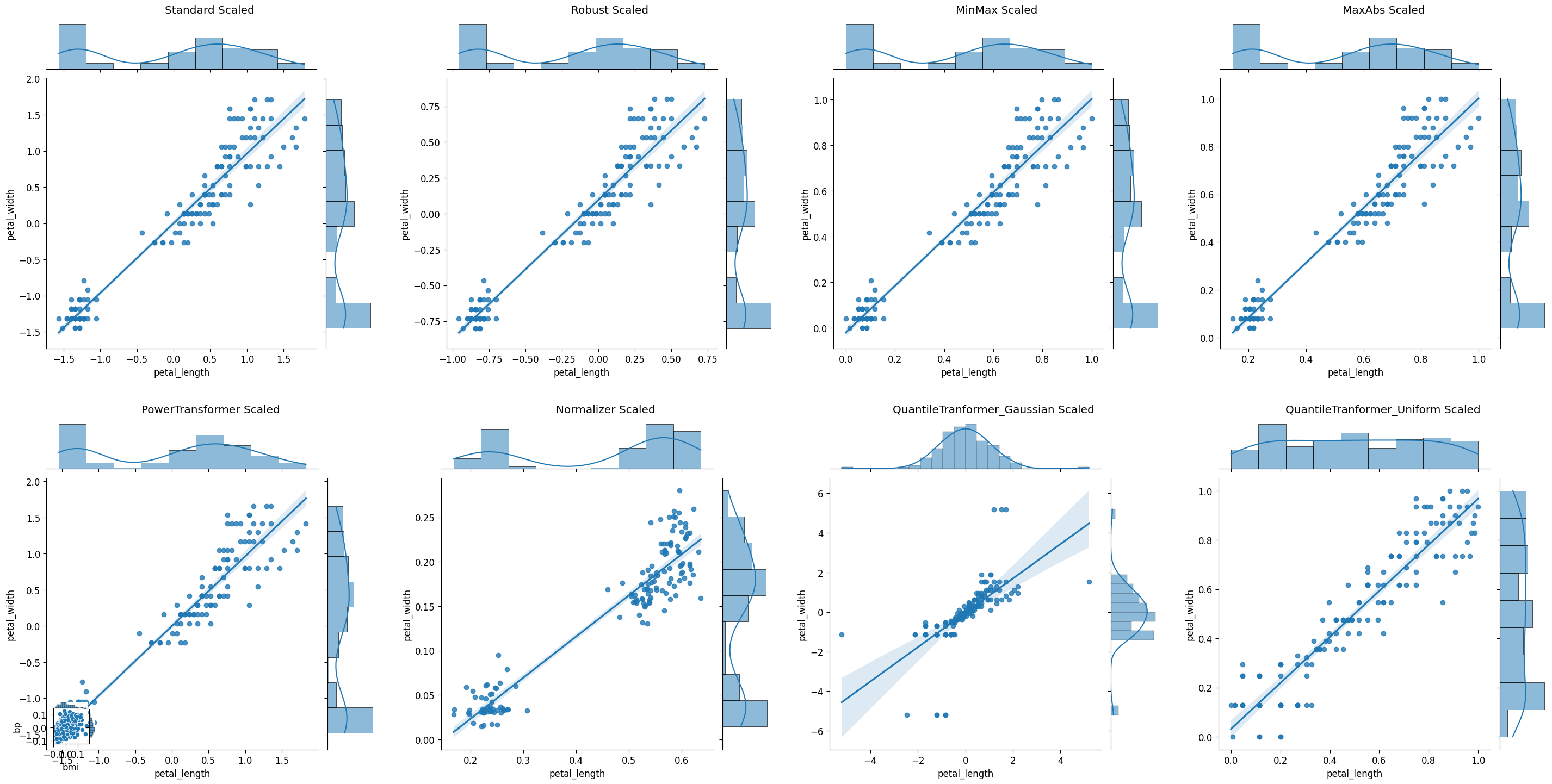
# 'bmi', 'bp', 's1', 's2' 열만 선택
selected_features = ['bmi', 'bp', 's3', 's6']
my_df = diabetes[selected_features]
# my_df 출력
print(my_df.head()) bmi bp s3 s6
0 0.0617 0.0219 -0.0434 -0.0176
1 -0.0515 -0.0263 0.0744 -0.0922
2 0.0445 -0.0057 -0.0324 -0.0259
3 -0.0116 -0.0367 -0.0360 -0.0094
4 -0.0364 0.0219 0.0081 -0.0466
STEP 2. 표준화 및 표준화 시각화
from sklearn.preprocessing import StandardScaler, RobustScaler
# Scaler 객체 생성
standard_scaler = StandardScaler()
robust_scaler = RobustScaler()
# 데이터 변환
my_df_standard = pd.DataFrame(standard_scaler.fit_transform(my_df), columns=my_df.columns)
my_df_robust = pd.DataFrame(robust_scaler.fit_transform(my_df), columns=my_df.columns)
# 결과 출력
print('Standard Scaled: \n', my_df_standard.describe()) # mean = 0, std = 1
print()
print('Robust Scaled: \n', my_df_robust.describe()) # median = 0, IQR = 1import seaborn as sns
import patchworklib as pw
pw.overwrite_axisgrid()
# 첫번째 그래프
g1 = sns.jointplot(data=my_df, x='bmi', y='bp', kind='reg')
g1 = pw.load_seaborngrid(g1)
g1.set_suptitle("Standard Scaled")
# 두번째 그래프
g2 = sns.jointplot(data=my_df, x='bmi', y='bp', kind='reg')
g2 = pw.load_seaborngrid(g2)
g2.set_suptitle("Robust Scaled")
# 그래프 합치기
g12 = (g1 | g2)
g12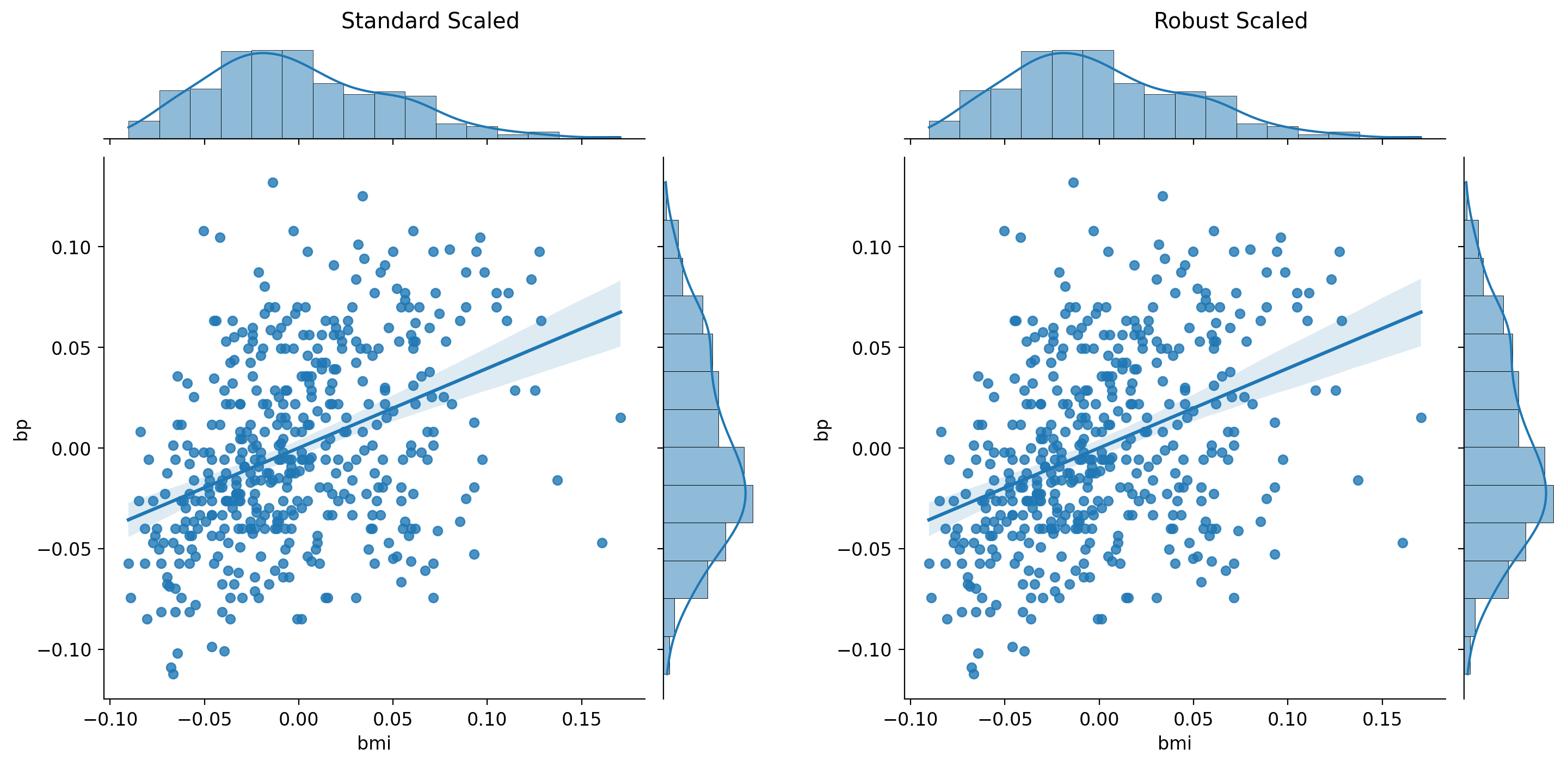
STEP 3. 정규화 및 정규화 시각화
from sklearn.preprocessing import MinMaxScaler, MaxAbsScaler
minmax_scaler = MinMaxScaler()
maxabs_scaler = MaxAbsScaler()
# 데이터 변환
my_df_minmax = pd.DataFrame(minmax_scaler.fit_transform(my_df), columns=my_df.columns)
my_df_maxabs = pd.DataFrame(maxabs_scaler.fit_transform(my_df), columns=my_df.columns)
# 결과 출력
print('MinMax Scaled (my_df): \n', my_df_minmax.describe()) # min = 0, max = 1
print()
print('MaxAbs Scaled (my_df): \n', my_df_maxabs.describe()) # min ~ 0, max = 1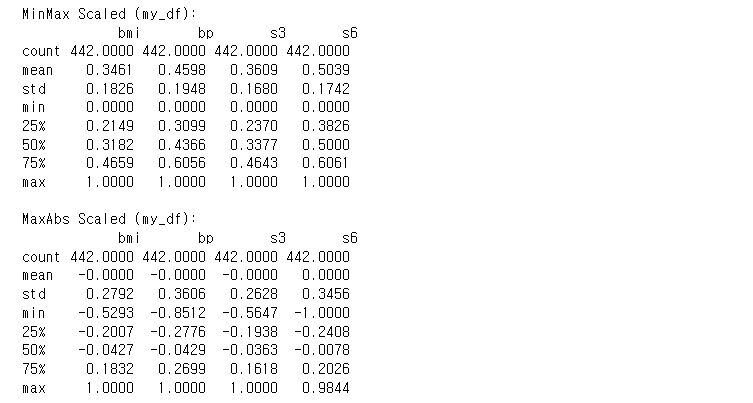
# 세번째 그래프
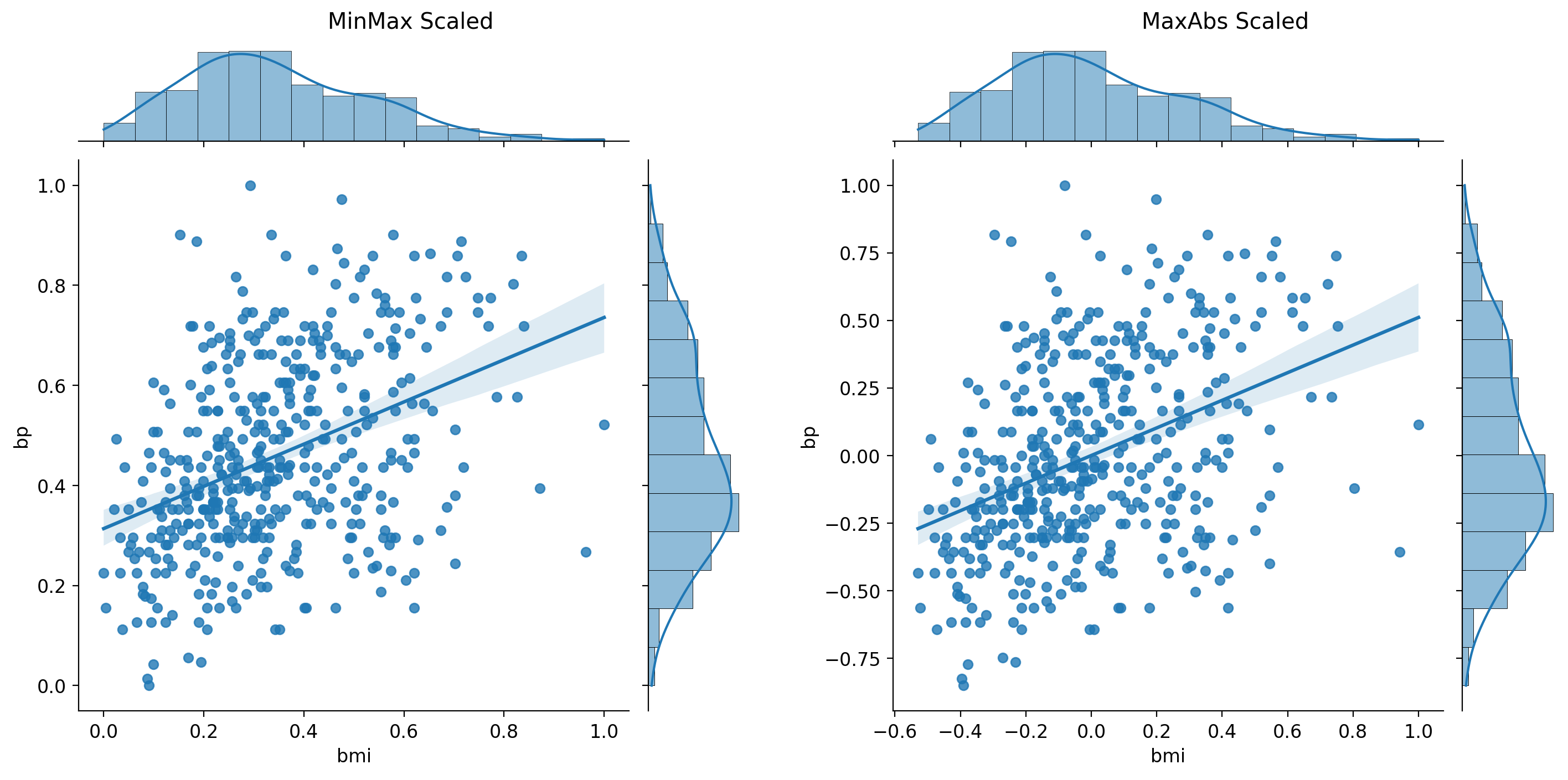
g3 = sns.jointplot(data=my_df_minmax, x='bmi', y='bp', kind='reg')
g3 = pw.load_seaborngrid(g3)
g3.set_suptitle("MinMax Scaled")
# 네번째 그래프
g4 = sns.jointplot(data=my_df_maxabs, x='bmi', y='bp', kind='reg')
g4 = pw.load_seaborngrid(g4)
g4.set_suptitle("MaxAbs Scaled")
# 그래프 합치기
g34 = (g3 | g4)
g34
STEP 4. 변환 및 변환 시각화
import numpy as np
from sklearn.preprocessing import PowerTransformer, Normalizer
# Scaler 객체 생성
power_scaler = PowerTransformer()
normal_scaler = Normalizer()
# 데이터 변환
my_df_power = pd.DataFrame(power_scaler.fit_transform(my_df), columns=my_df.columns)
my_df_normal = pd.DataFrame(normal_scaler.fit_transform(my_df), columns=my_df.columns)
# 결과 출력
print('PowerTransformer Scaled (my_df): \n', my_df_power.describe())
print()
print('Normalizer Scaled (my_df): \n', my_df_normal.describe())
print('Euclidean Distance from 0 (my_df): \n', np.linalg.norm(my_df_normal, axis=1))
# 다섯번째 그래프
g5 = sns.jointplot(data=my_df_power, x='bmi', y='bp', kind='reg')
g5 = pw.load_seaborngrid(g5)
g5.set_suptitle("PowerTransformer Scaled")
# 여섯번째 그래프
g6 = sns.jointplot(data=my_df_normal, x='bmi', y='bp', kind='reg')
g6 = pw.load_seaborngrid(g6)
g6.set_suptitle("Normalizer Scaled")
# 그래프 합치기
g56 = (g5 | g6)
g56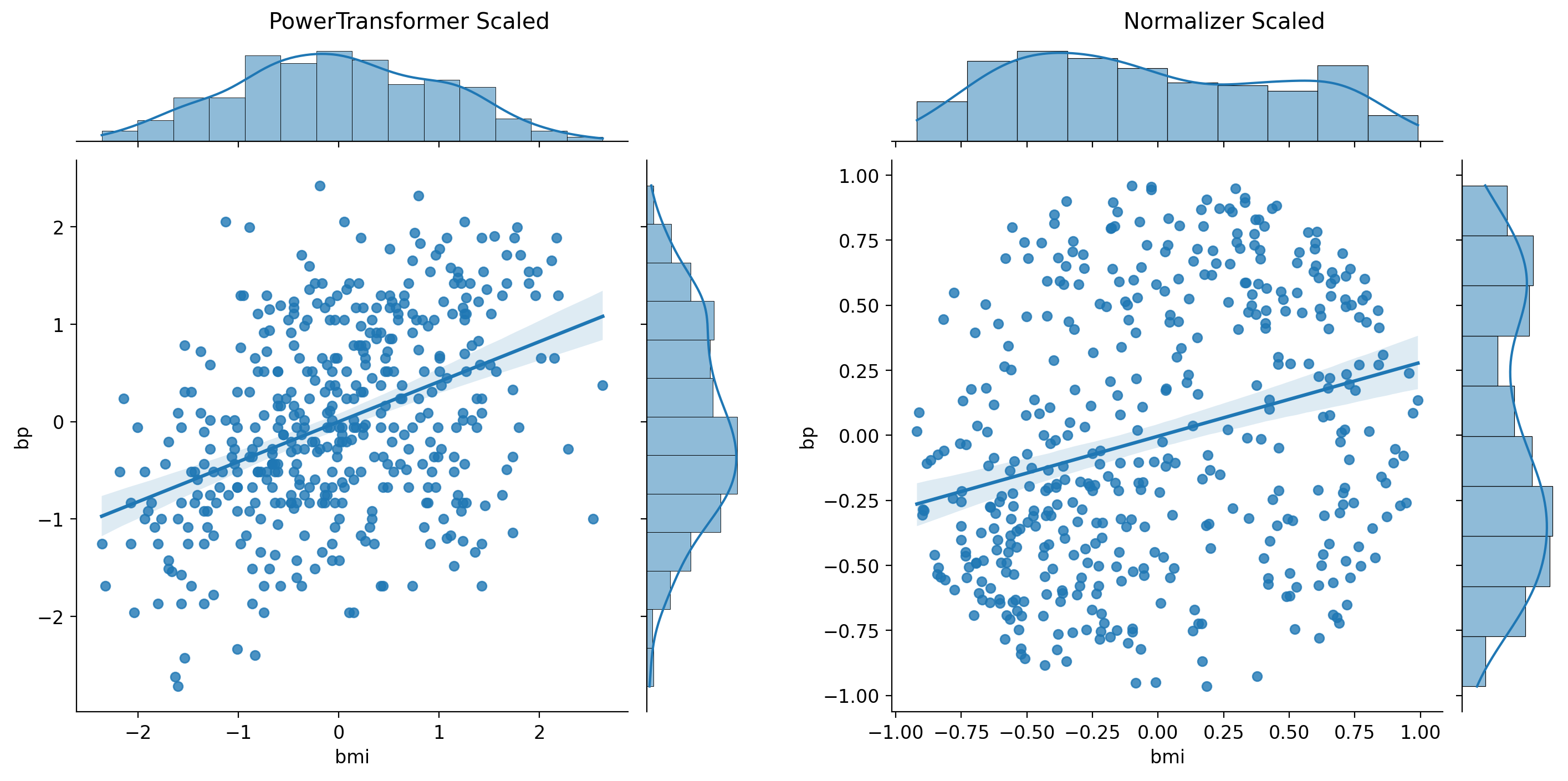
from sklearn.preprocessing import QuantileTransformer
# Scaler 객체 생성
gaussian_scaler = QuantileTransformer(output_distribution='normal')
uniform_scaler = QuantileTransformer(output_distribution='uniform')
# 데이터 변환
my_df_gaussian = pd.DataFrame(gaussian_scaler.fit_transform(my_df), columns=my_df.columns)
my_df_uniform = pd.DataFrame(uniform_scaler.fit_transform(my_df), columns=my_df.columns)
# 결과 출력
print('QuantileTranformer_Gaussian Scaled (my_df): \n', my_df_gaussian.describe())
print()
print('QuantileTranformer_Uniform Scaled (my_df): \n', my_df_uniform.describe())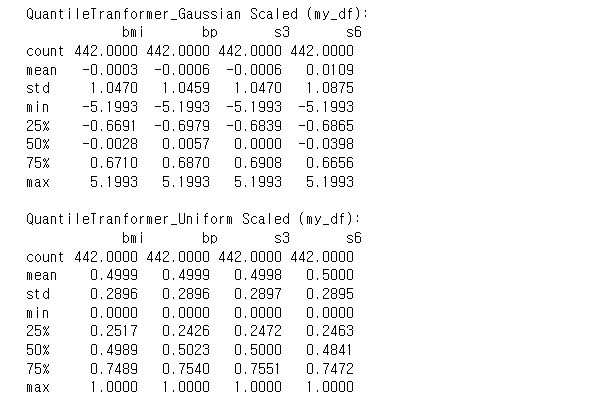
# 일곱번째 그래프
g7 = sns.jointplot(data=my_df_gaussian, x='bmi', y='bp', kind='reg')
g7 = pw.load_seaborngrid(g7)
g7.set_suptitle("QuantileTranformer_Gaussian Scaled")
# 여덟번째 그래프
g8 = sns.jointplot(data=my_df_uniform, x='bmi', y='bp', kind='reg')
g8 = pw.load_seaborngrid(g8)
g8.set_suptitle("QuantileTranformer_Uniform Scaled")
# 그래프 합치기
g78 = (g7 | g8)
g78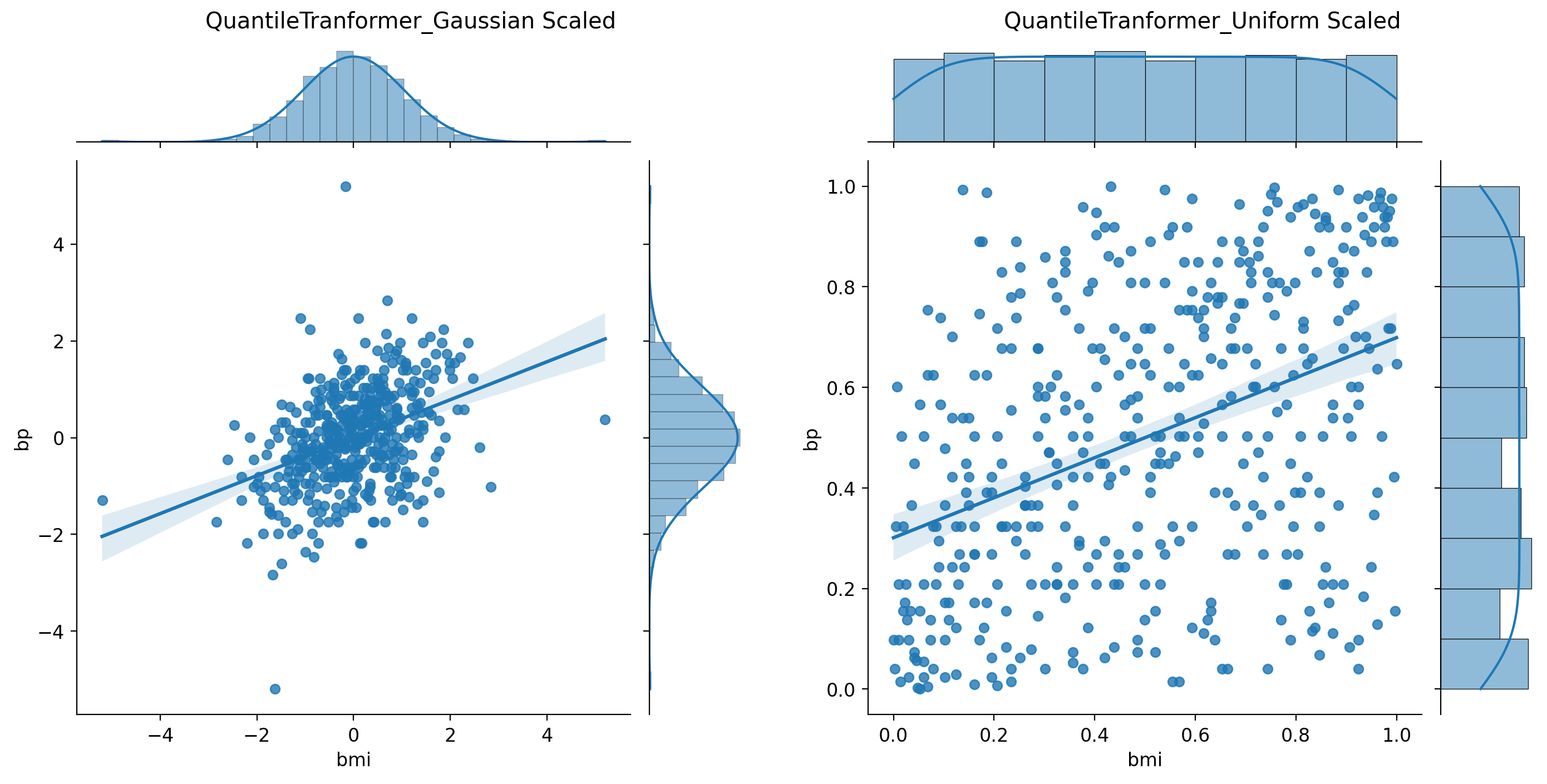
STEP 5. 모든 스케일링 합치기
(g1|g2|g3|g4)/(g5|g6|g7|g8)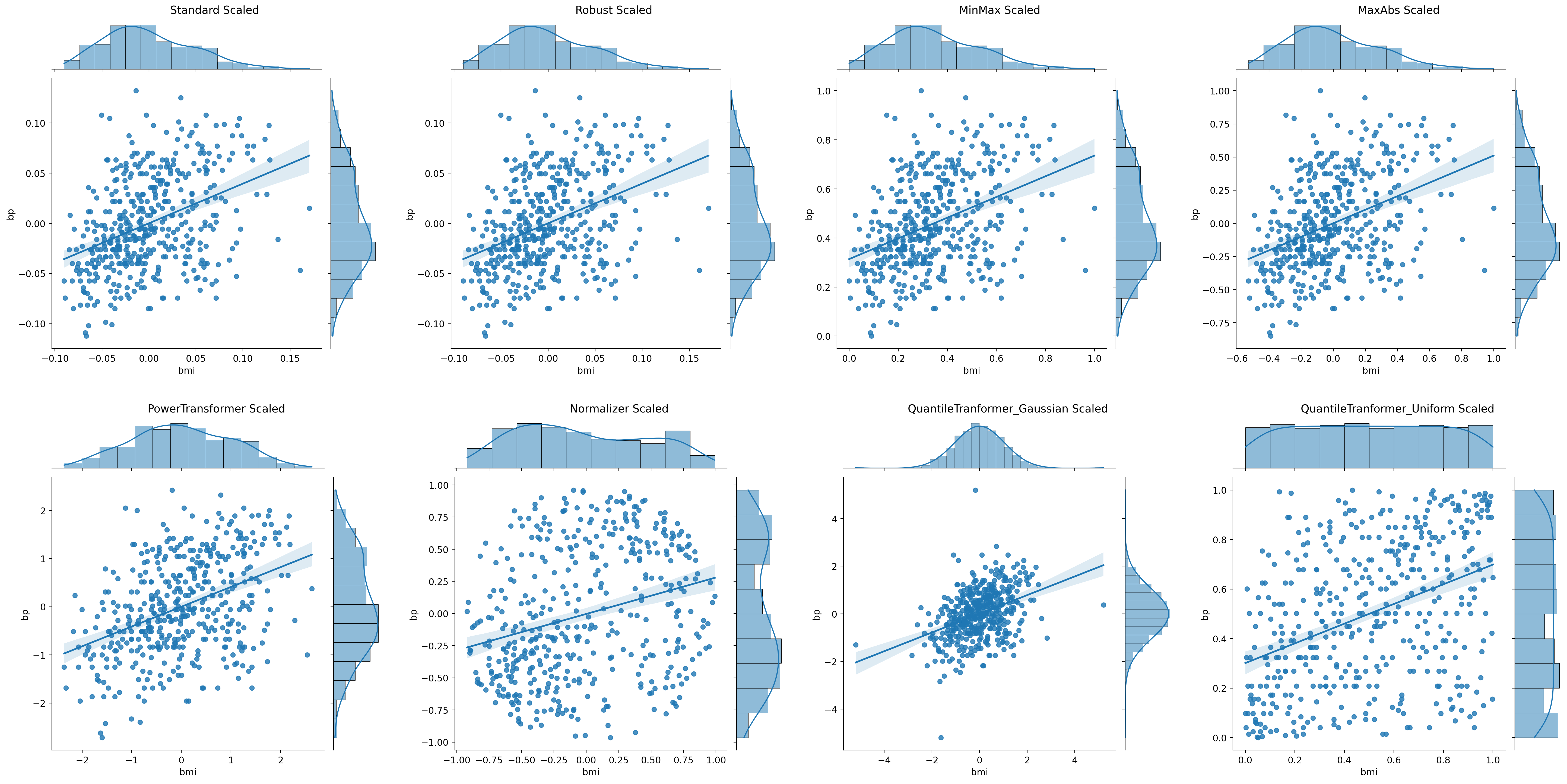
STEP 6. 스케일링 전 후 회귀분석 비교하기
- 정규화를 적용하였을 때 모형의 성능이 향상됨
- 반면 Power Transformer 활용시 성능이 저하됨
1. 데이터 불러오기
from sklearn.datasets import load_diabetes
# 당뇨병 데이터셋 불러오기
diabetes = load_diabetes()
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error2. 데이터 학습 준비
# 데이터 준비
X = diabetes.data
y = diabetes.target
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)3. 스케일링 없이 회귀분석
# 회귀 모델 학습 (스케일링하지 않은 데이터)
model_unscaled = LinearRegression()
model_unscaled.fit(X_train, y_train)
# 테스트 데이터에 대한 예측
y_pred_unscaled = model_unscaled.predict(X_test)
# 평가 (스케일링하지 않은 데이터)
mse_unscaled = mean_squared_error(y_test, y_pred_unscaled)
print(f'Mean Squared Error (Unscaled): {mse_unscaled}')Mean Squared Error (Unscaled): 2900.193628493482
4. Power Transformer 적용
# Power Transformer 스케일링 적용
power_scaler = PowerTransformer()
X_train_power = power_scaler.fit_transform(X_train)
X_test_power = power_scaler.transform(X_test)
# 회귀 모델 학습 (Power Transformer 스케일링)
model_power = LinearRegression()
model_power.fit(X_train_power, y_train)
# 테스트 데이터에 대한 예측
y_pred_power = model_power.predict(X_test_power)
# 평가 (Power Transformer 스케일링)
mse_power = mean_squared_error(y_test, y_pred_power)
print(f'Mean Squared Error (Power Transformer Scaled): {mse_power}')Mean Squared Error (Power Transformer Scaled): 2982.383365720045
5. Normalizer 적용
normal_scaler = Normalizer()
X_train_normal = normal_scaler.fit_transform(X_train)
X_test_normal = normal_scaler.transform(X_test)
# 회귀 모델 학습 (Normalizer 스케일링)
model_normal = LinearRegression()
model_normal.fit(X_train_normal, y_train)
# 테스트 데이터에 대한 예측
y_pred_normal = model_normal.predict(X_test_normal)
# 평가 (Normalizer 스케일링)
mse_normal = mean_squared_error(y_test, y_pred_normal)
print(f'Mean Squared Error (Normalizer Scaled): {mse_normal}')Mean Squared Error (Normalizer Scaled): 2871.268277996966

