서론
코딩테스트에서 2번 혹은 3번 쯤에 자주 위치하는 유형이다.
dp와 관련하여 여러 자료들과 설명이 많지만 내가 이해하기 좋은 방향으로 개념의 재구성을 해보려고 한다.
핵심
- DP는 [점화식]이다.
- DP는 [O(N)]으로 구현해야할 때 사용한다.
1. 점화식
DP를 공부하다보면 memoization이라는 용어를 접할 것이다.
"이전 상태를 기억하여 현재 상태를 갱신한다."
라는 뜻인데 ...
사실 나는 이를 처음 공부할 때 별로 와닿지가 않았다.
그래서 나는 점화식 으로 이해했다.
점화식이란?
[x0,x1,x2,...,xn-1,xn]이 있을 때 "xn = f(n-1) + ?"의 형태로 표현되는 식을 말한다.
혹시라도 이해가 안 갈까봐 예시를 준비했다.
등차수열
1,3,5,7,9,... 의 수열은 점화식으로 표현하면 아래와 같다.
f(x) = f(x-1) + 2
피보나치 수열
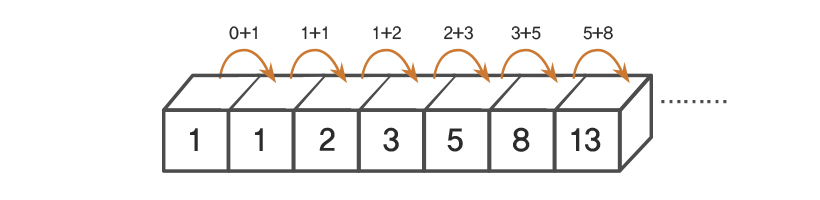
피보나치 수열을 점화식으로 표현하면 어떻게 될까?
fibo(n) = fibo(n-1) + fibo(n-2)
n-2와 n-1의 값을 참조하여 n의 값을 정한다.
DP도 위와 마찬가지다.
등차수열을 파이썬 코드로 표현하면
dp = [1,1,1,1,1]
for i in range(1,len(dp)):
dp[i] = dp[i-1] + 2피보나치 수열을 파이썬 코드로 표현하면
dp = [1,1,1,1,1,1,1]
for i in range(2,len(dp)):
dp[i] = dp[i-1] + dp[i-2]2. 사용 용도
DP는 코딩테스트 문제를 O(N)으로 풀어야 할 때 사용한다.
파이썬 기준으로 1초에 10^8 정도의 연산이 가능하다.
예를 들어, 어떤 문제의 입력 조건이 N = 10^5이라고 할 때 이 문제는 O(N^2)으로 풀면 시간초과가 발생한다.
🔥 예제 문제로 아래를 풀어보자.
