scikit-learn

• numpy
• pandas
• scipy

Deep Learning

• numpy
• pandas
• scipy
• Tensorflow
• PyTorch

가설 검정

가설

⭐️ 귀무가설(Null Hypothesis)

• 통계에서의 가설 검정은 측정된 두 현상 간에 관련이 없다는 귀무가설(Null Hypothesis, 𝐻_0
  로 표시)

• '관련이 없다'라는 형태의 가설

• 두 변수가 독립이다.두변수의 평균에 차이가없다.동전을 던졌을때 앞면이 나올 확률과 뒷면이 나올 확률에 차이가 없다. 특정 약이 질병 치료에 효과가 없다. 올해 제품의 생산량과 작년의 생산량이 같다.

• 법정으로 비유하면 증거 불충분. 무죄추정의 원칙

⭐️ 대립가설(Alternative Hypothesis)

• 두 현상간에 '관련이 있다'라고 보는 것으로 연구자가 알아보고자 하는 가설인 대립가설
  (Alternative Hypothesis; 𝐻_1로 표시)
• 두 변수가 독립이 아니다. 두변수의 평균에 차이가있다. 동전의 앞면이나올 확률이 동전의 뒷면이 나올 확률과 다르다. 특정 약]이 질병 치료에 효과가 있다. 올해 제품의 생산량과 작년
  의 생산량이 다르다.
• 대립가설은 같지않다/작다/크다 세가지 형태로 나타낼 수 있다.
• 대립가설은 귀무가설하고 다르게 피고가 유죄라고 판단

⭐️ 제1종의오류와 제2종의오류

• 제1종의오류:귀무가설이 옳은데도 불구하고 그것을 버려버리는 잘못
  □ 실제로는 참이지만 연구결과 거짓이라고 나오는 경우

• 제2종의오류:귀무가설이 잘못되었는데도 그것을버리지못한잘못
  □ 실제로는 거짓인데 연구결과 참으로 나오는 경우

귀무가설

Null Hypothesis

일단 관련이 없다고 가정

집단1 평균 = 집단2 평균

대립가설

Alternative Hypothesis

일단 관련이 있다고 가정

집단1 평균 != 집단2 평균

p-value < 0.05 : 대립가설을 받아들임
p-value > 0.05 : 귀무가설 받아들임

접근 방식

1. 독립적인 두 데이터 집합을 비교하고자 한다.
2. 두 데이터 집합의 표준편차가 같은지에 대해서는 아무런 가정도 하지 않는다.
3. 귀무가설은 데이터 집합들의 모집단 평균들이 서로 같다는 것

• 모집단 평균들을 알지 못하므로, 표본 평균들과 표본 표준편차들을 사용해서 승인할지 기각할지 판정하는데 필요한 증거를 얻는다.

4. 가설검정은 데이터가 독립동일분포라고 가정한다. 위의 예제도 독립동일분포라고 가정

t-분포

💡 적은 양의 데이터로 모집단을 유추하고 싶을 때 사용한다.

• t로 표기하는 검정 통계량에 의존한다.
• 미리 만들어진 t-분포와 비교해서 p-값을 구한다.
• t-검정은 모수적 검정의 일종이다. 모수적 검정이라는 것은 검정할 데이터와 데이터의 분포에 관해 특정한 가정들을 둔다는 뜻

검정 방법

• t분포를 이용한 정규모집단의 모평균 추정법

1단계
○ 얻은 n개의 표본에서 표본평균 x'와 표본표준편차 s를 계산한다.

2단계
○ 표본평균 x'와 표본표준편차 s, 추정하려고 하는 모평균 μ를 사용하여 자유도 n-1인 t분포를 따르는 통계량 T를 다음과 같이 계산

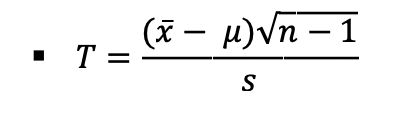
3단계
○ 자유도 n-1인 95% 예언적중구간을 선택해서 −α ≤ T ≤ α라 하는 95% 예언적중구간을 만든다.

○ 4단계

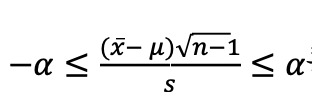
위 공식을 𝜇에 대해서 풀면, 이것이 95% 신뢰구간이다.