문제 소개

대표적인 문제로 백준의 평범한 배낭 문제가 있다.

라벨링

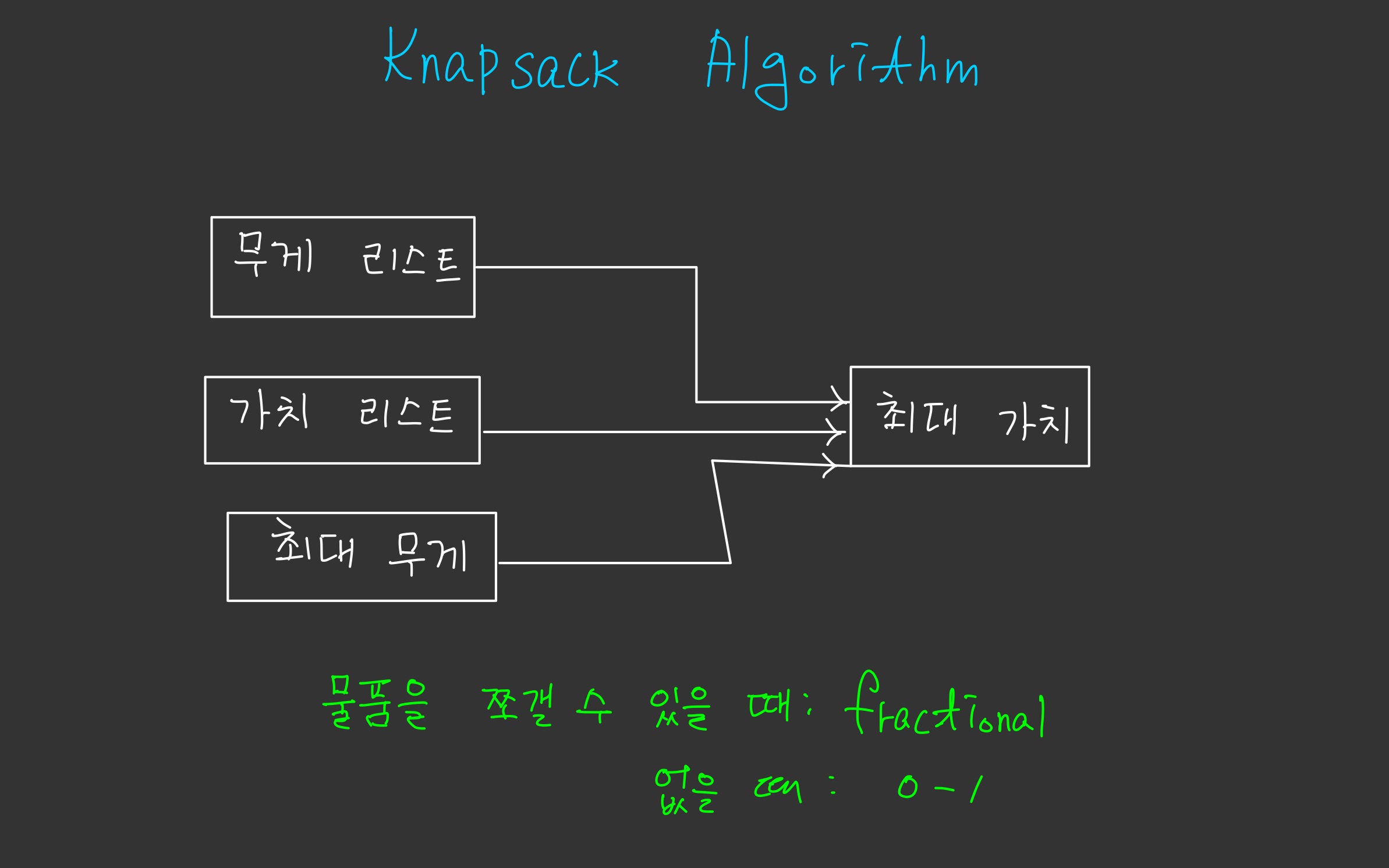
냅색 알고리즘은 다음과 같은 조건/문제에서 가져다 쓴다.

• 조건: 무게 리스트, 가치 리스트, 최대 무게
• 문제: 최대 가치

이 때, (무게,가치)를 지닌 물품을 쪼갤 수 있을 때(설탕 같이) fractional로 접근하고 쪼갤 수 없을 때는 0-1 냅색으로 접근한다.

0-1 냅색 (DP)

2차원 배열

동작 설명

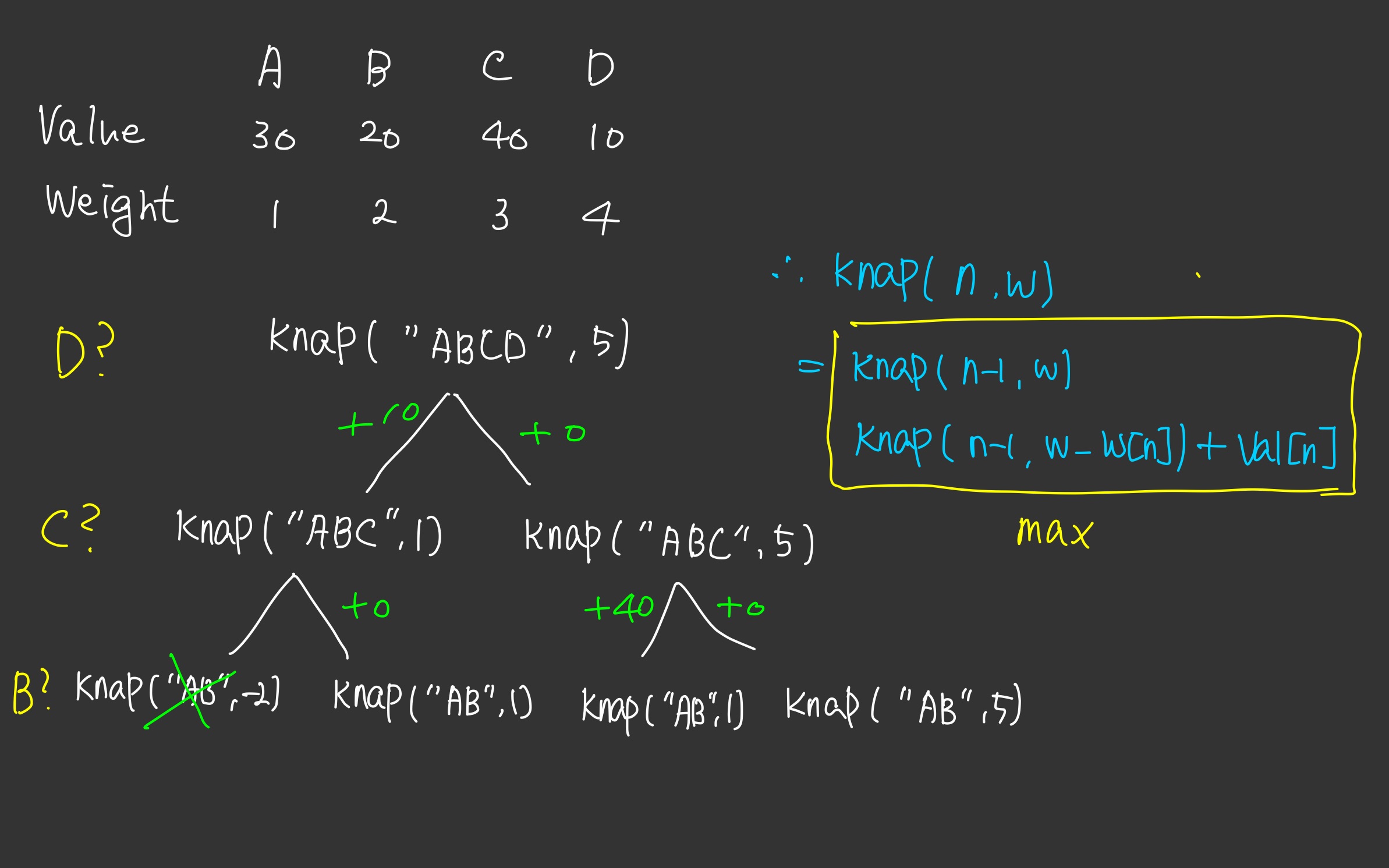
물품 A,B,C,D와 (가치,무게) 순서쌍이 주어졌다고 하자.

이 때 최종적인 점화식은 노란색 박스와 같이 된다. 왜일까?

1. knap("ABCD",5) = 물품 A,B,C,D를 다 체크해봤고 총 무게는 5kg이다.

2. knap("ABC",1) = 물품 A,B,C를 체크해봤고 총 무게는 1kg이다.

3. knap("ABC",5) = 물품 A,B,C를 체크해봤고 총 무게는 5kg이다.

4. knap("AB",-2) = 물품 A,B를 체크해봤고 총 무게는 -2kg이다.
   음수 무게는 불가능하므로 나머지 서브트리는 확인 불필요

5. knap("AB",1) = 물품 A,B를 체크해봤고 총 무게는 1kg이다.

6. knap("AB",5) = 물품 A,B를 체크해봤고 총 무게는 5kg이다.

어느 정도 감이 오는가? 위를 토대로 그림을 해석하면 다음과 같다.

1번 항목은 총 무게 5kg으로 모든 물품을 검사해본 상태이다.

거기서 D가 포함되어 있는가를 묻는다.

포함되어 있다면 D의 무게 4kg 만큼 빼주고 가치를 올려준다.
그렇지 않다면 무게와 가치는 그대로이다. 같은 원리로 계속 진행한다.

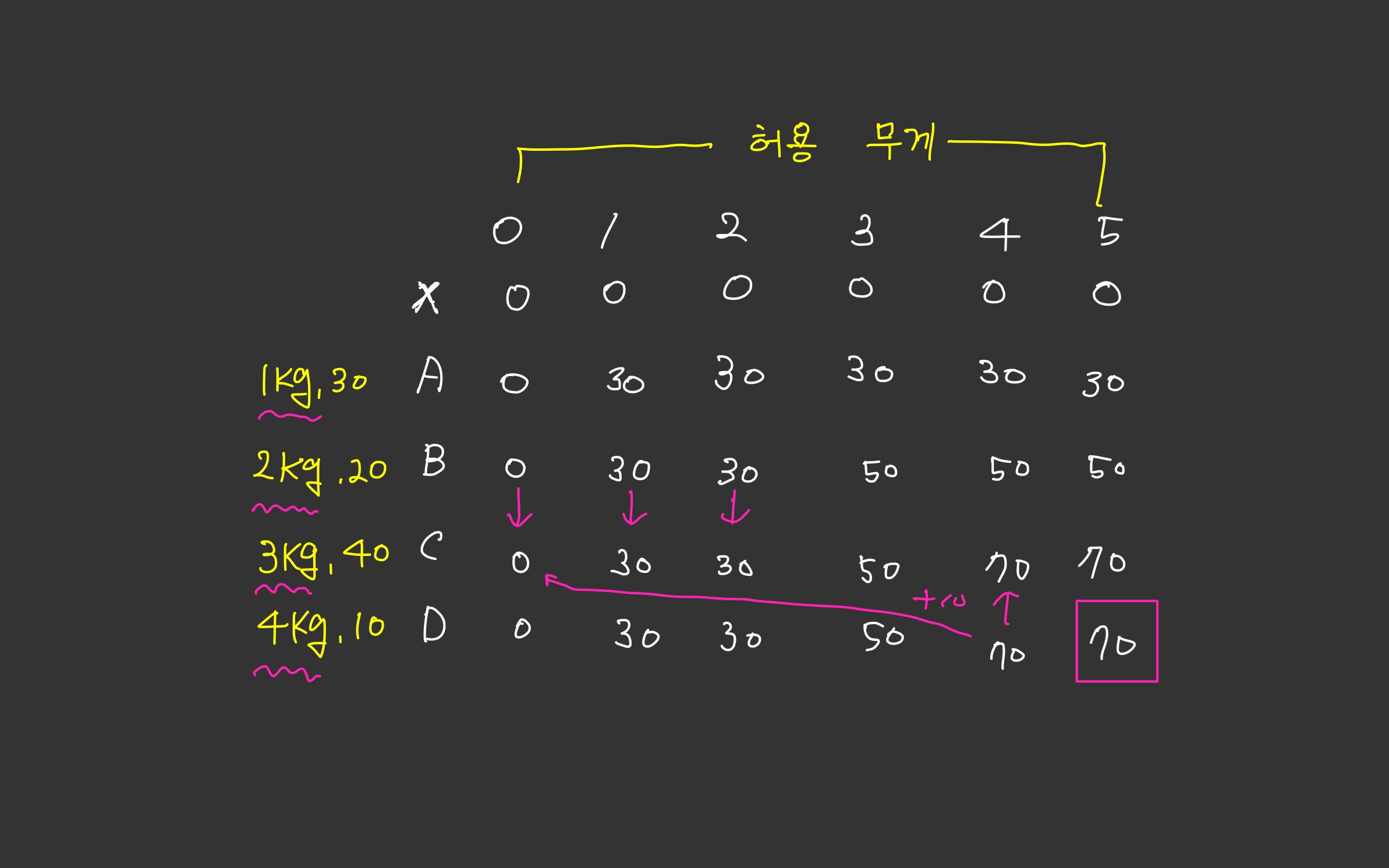
2차원 배열 진행 과정

위 설명으로도 이해가 가지 않는다면 아래의 진행 과정을 살펴보자.

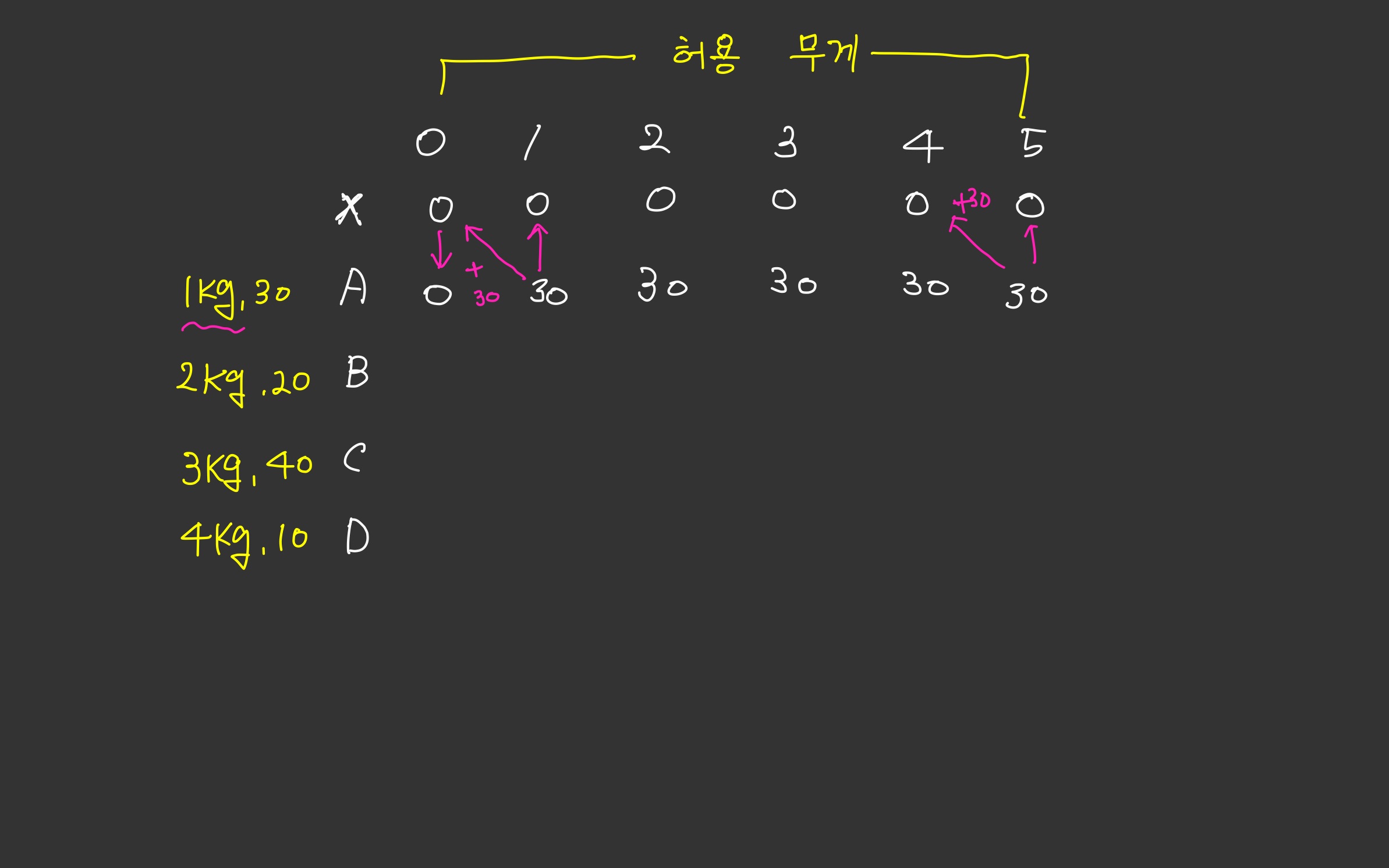
허용 무게와 물품 테이블을 생성한다. 이 때 아무것도 선택하지 않을 경우에는 어떠한 가치도 얻을 수 없으므로 0으로 초기화를 시킨다.

첫 번째 아이템 A를 보자. 무게는 1kg이고 가치는 30이다.
허용 무게가 0kg일 때는 A를 선택할 수 없으므로 이전 값을 그대로 가져온다.
허용 무게가 1kg부터는 A를 선택하는 경우와 그렇지 않은 경우로 나뉜다.
2개의 경우의 수 중 최대 가치를 골라야 하는데 먼저 선택하는 경우부터 보자.
A를 선택하는 경우는 반드시 A의 무게만큼 허용 무게를 확보해 놓아야 한다.
따라서 허용 무게에서 A의 무게만큼 뺀 지점에서의 최대 가치에서 A를 획득했을 때의 가치를 더한다. 이것을 파이썬으로 표현하면

val[i-1]+K[i-1][w-wt[i-1]]

이렇게 된다. 나머지 과정도 비슷한 원리로 계속 수행시켜 나가면 된다.

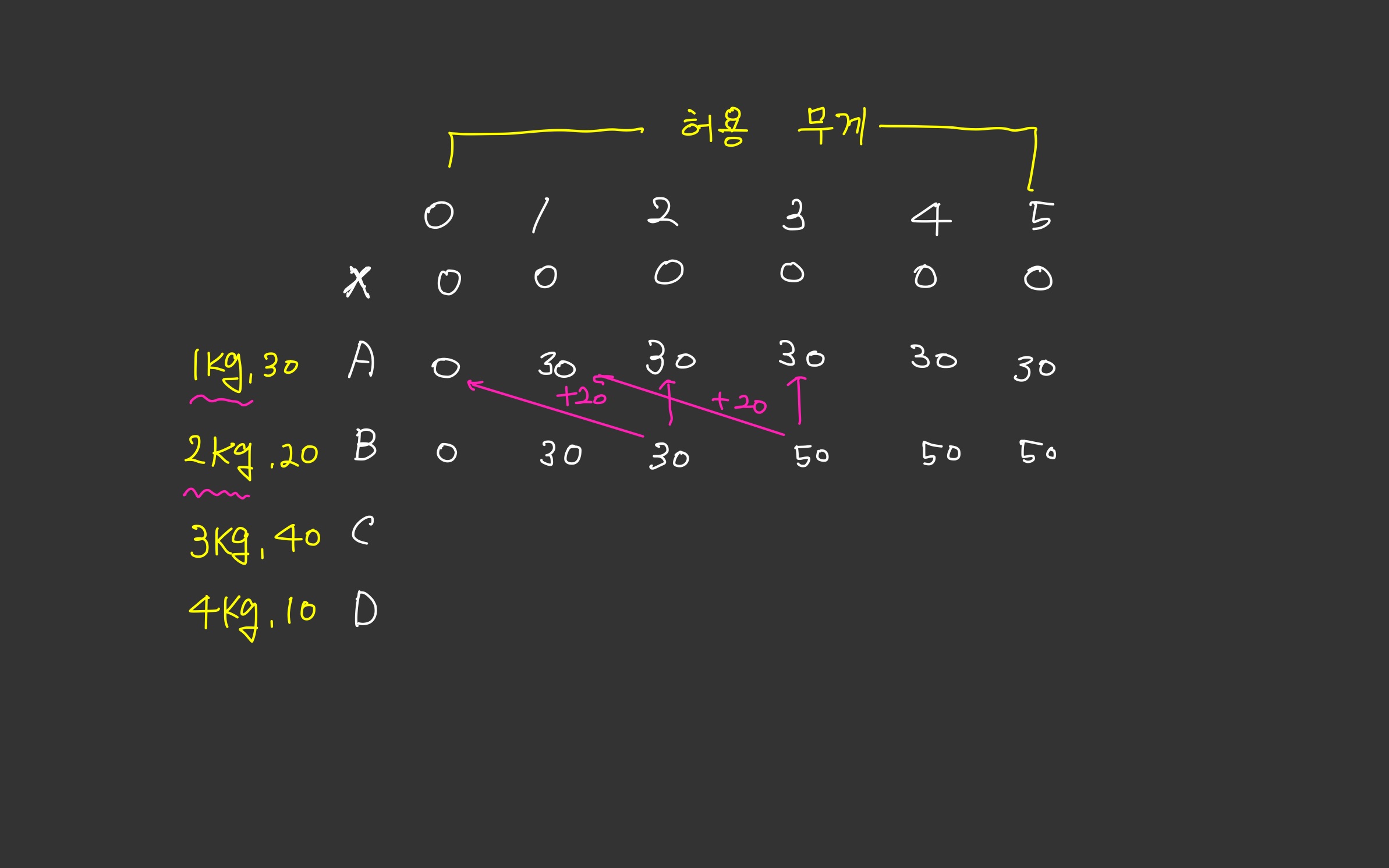
코드

def knapSack(W, wt, val, n):
    K = [[0 for x in range(W + 1)] for x in range(n + 1)]
 
    # Build table K[][] in bottom up manner
    for i in range(n + 1):
        for w in range(W + 1):
            if i == 0 or w == 0:
                K[i][w] = 0
            elif wt[i-1] <= w:
                K[i][w] = max(val[i-1]
                          + K[i-1][w-wt[i-1]], 
                              K[i-1][w])
            else:
                K[i][w] = K[i-1][w]
 
    return K[n][W]

1차원 배열

위의 점화식을 그대로 이어받아 공간복잡도를 줄일 수도 있다.

코드

def knapSack(W, wt, val, n):
    dp = [0 for i in range(W+1)]  # Making the dp array
 
    for i in range(1, n+1):  # taking first i elements
        for w in range(W, 0, -1):  # starting from back,so that we also have data of
                                # previous computation when taking i-1 items
            if wt[i-1] <= w:
                # finding the maximum value
                dp[w] = max(dp[w], dp[w-wt[i-1]]+val[i-1])
 
    return dp[W]  # returning the maximum value of knapsack

WHY?

왜 무게의 범위가 W부터 1까지 거꾸로 가는 걸까?

2차원 배열과 달리 1차원 배열은 이전 값을 참고할 수가 없다.

따라서 1부터 W까지 순차적으로 진행하면 dp[w-wt[i-1]]에서 값 중첩의 오류가 발생한다.

Fractional 냅색

그리디하게 풀면 된다.

# Main greedy function to solve problem
def fractionalKnapsack(W, arr):
 
    # Sorting Item on basis of ratio
    arr.sort(key=lambda x: (x.value/x.weight), reverse=True)   
 
    # Result(value in Knapsack)
    finalvalue = 0.0
 
    # Looping through all Items
    for item in arr:
 
        # If adding Item won't overflow,
        # add it completely
        if item.weight <= W:
            W -= item.weight
            finalvalue += item.value
 
        # If we can't add current Item,
        # add fractional part of it
        else:
            finalvalue += item.value * W / item.weight
            break
     
    # Returning final value
    return finalvalue