문제 링크

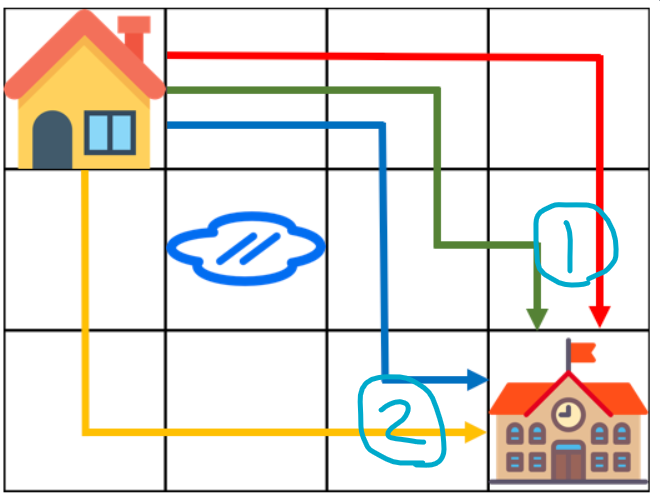
풀이

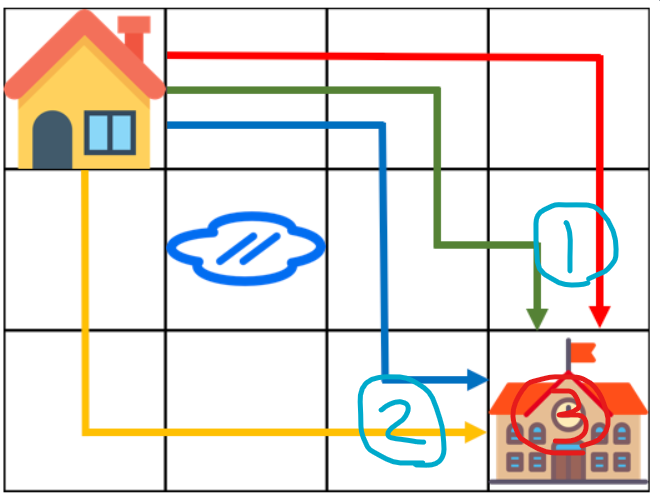
[1번까지 올 수 있는 최단 경로]+[2번까지 올 수 있는 최단 경로]
= [3번까지 올 수 있는 최단 경로]

dp[i][j]: (i,j)까지 올 수 있는 최단 경로
라고 정의했을 때 점화식은 다음과 같이 유도된다.

dp[i][j] = dp[i-1][j]+dp[i][j-1]

(📌 문제는 (열,행)으로 표기를 했지만 나는 (행,열)로 풀었다.)

0행 / 0열을 먼저 처리해준 이유

하기 코드를 참조하면 dp 순환은 (1,1)부터 시작한다.

그 이유는 0행과 0열은 위 혹은 왼쪽 칸이 없기 때문이다.

따라서, 물웅덩이를 고려하여 0행과 0열의 각 칸에 대하여 최단 경로를 먼저 처리해주고 dp를 돌린다.

코드

INF = 1000000007
def solution(m, n, puddles):
    dp = [[1]*m for _ in range(n)]
    # Base Case
    for (i,j) in puddles:
        dp[j-1][i-1] = 0
    
    for i in range(n):
        if not dp[i][0]:
            for j in range(i+1,n):
                dp[j][0] = 0
    for i in range(m):
        if not dp[0][i]:
            for j in range(i+1,m):
                dp[0][j] = 0
            
    # General Case
    for i in range(1,n):
        for j in range(1,m):
            if dp[i][j] != 0:
                dp[i][j] = (dp[i-1][j]%INF+dp[i][j-1]%INF)%INF
    return dp[n-1][m-1]%INF