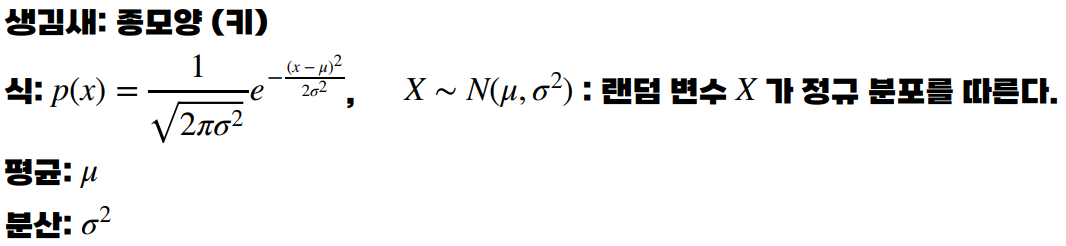랜덤 변수와 확률 분포

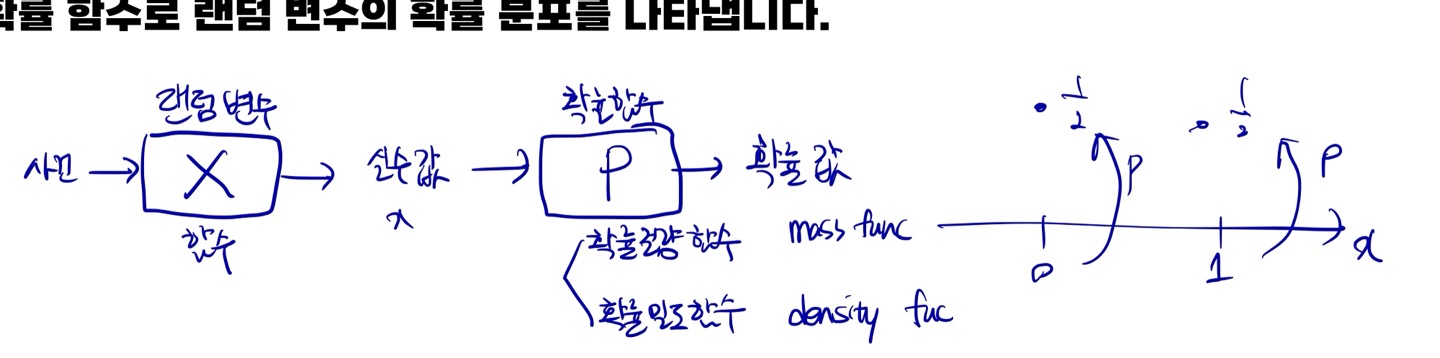
랜덤 변수는 함수이다. 즉, 사건이 발생했을 때 실수값으로 나타내는 함수이다. 이러한 실수값을 확률값으로 나타내는 것이 확률 함수이다. 확률 함수는 확률 질량 함수와 확률 밀도 함수가 있다. 확률 함수로 랜덤 변수의 확률 분포를 나타낸다. 정리하면 아래의 그림과 같다.

평균과 분산

확률 분포를 설명하는 두 가지 대푯값이다.

평균은 mean, average라고도 하지만, 여기서는 expectation 기댓값을 다룰 것이다.
어떠한 시행을 무한번하고 산술 평균을 구하면 기댓값과 같아진다.
기댓값의 정의는 랜덤 변수 X에 대해서 $E[X]=\sum_ix_ip_i$, 연속 랜덤 변수에서는 정적분의 정의에 따라 $\int_{-\infin}^{\infin}xp(x)dx, E[X]=\mu$이다.

확률값을 곱해주는 것은 "weighted average"라고 생각하면된다. 랜덤 변수가 무수히 많은 시행을 거쳤을 때 각 사건에 대해 확률값을 곱해줌으로써 기댓값은 하나의 값으로 표현할 수 있다.

분산은 퍼진 정도로 이해하면 된다. 이산적일때는 $V[X]=\sum_i(x_i-\mu)^2p_i$이고, 연속적일때는 $V[X]=\int_{-\infin}^{\infin}(x-\mu)^2p(x)dx$ 이다. 기댓값을 구할 때와 동일하게 편차의 값을 대입해주면 된다.

균등 분포와 정규 분포

균등 분포(Uniform distribution)는 평평하다!

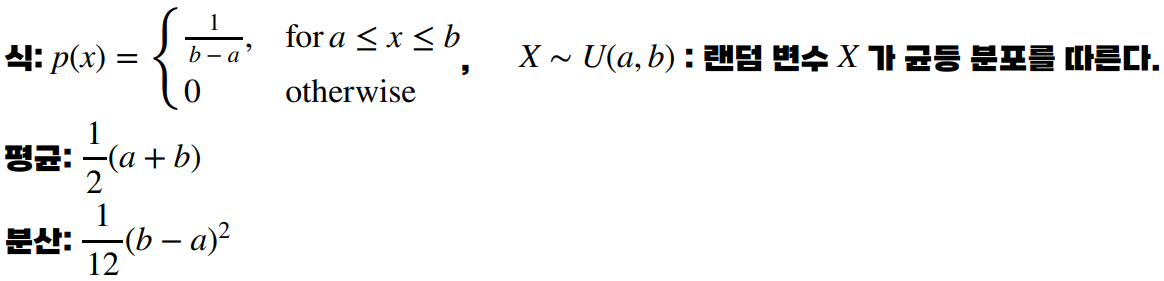
정규분포(Normal distribution or Gaussian distribution)은 종모양이다.