Likelihood, MLE, MAP 완전 정복

함지율·2024년 4월 23일

AI Deep Dive

목록 보기

3/3

이 포스트는 이형민, 미남로그 님의 블로그를 바탕으로 작성하였습니다.

서론

Bayes Rule을 이용한 방식의 가장 큰 단점들 중 하나는 Likelihood의 Probability Distribution을 알아야 한다는 점이다. 그래서 우리는 Data로부터 직접 decision policy를 얻고자 한다. 정해지지 않은 몇 개의 parameter로 이루어진 함수로 모델링을 한 후에, 이 모델이 주어진 Data를 가장 잘 설명하도록 parameter들을 구해낼 수 있다면 어떨까? 사실 이러한 방식을 이용하는 대표적인 알고리즘이 바로 Deep Learning 이다. 그리고 이 Deep Learning의 기본적인 Loss Function들은 대부분 Maximum Likelihood Estimation(MLE)과 Maximum A Posterior(MAP)를 통해 증명된다. 또한 확률을 기반으로 하기 때문에 이 두 이론을 공부하고 나면 확률과 Deep Learning 사이의 연결고리를 파악하는 데 큰 도움이 될 것이다. 그러면 MLE와 MAP에 관해 본격적으로 알아보도록 하자!

Prior, Likelihood, Posterior

대부분의 머신러닝 알고리즘에서 주어진 대상은 당연히 Dataset, D이다. 그리고 구하고자 하는 대상은 모델의 parameter $w$ 이다.

Posterior: 주어진 대상이 주어졌을 경우, 구하고자 하는 대사의 확률 분포. 이 포스트에서는 $p(w|D)$ .
Likelihood: 구하고자 하는 대상을 모르지만 안다고 가정했을 경우, 주어진 대상의 분포. 이 포스트에서는 $p(D|w)$ . $w$ 를 모르기 때문에 $w$ 에 대한 함수 형태로 나올 것이다.
Prior: 주어진 대상들과 무고나하게, 상식을 통해 우리가 구하고자 하는 대상에 대해 이미 알고 있는 사전 정보. 연구자의 경험을 통해 정해주어야 한다. 이 포스트에서는 $p(w)$ .

Basyes Rule

관측 A에 따른 결과 B가 나온다고 했을 때, 베이지안 룰을 다음 수식과 같다.

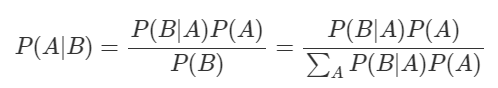
분모 $P(B)$ 는 전체 확률의 법칙(Law of Total Probability)에 의해서 유도된다.

전체 확률의 법칙은 위키피디아에 다음과 같이 증명하였다.

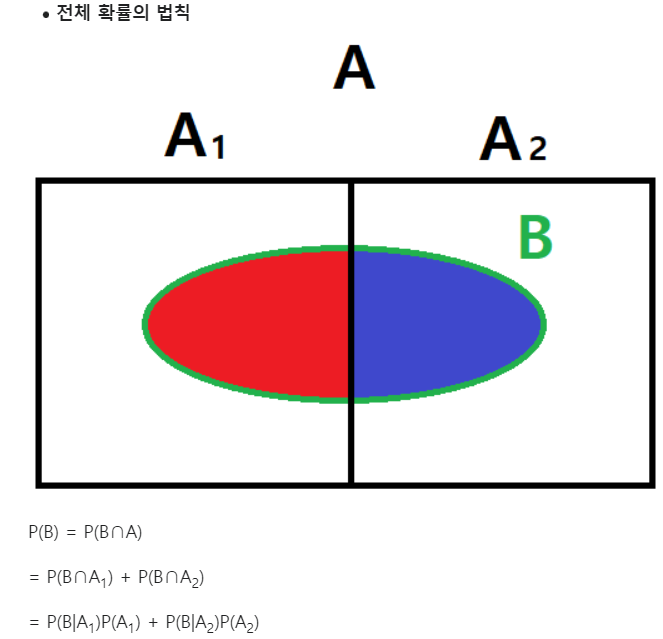
따라서 A대신 $w$ , B 대신 $x$ 를 넣으면 다음과 같이 된다.

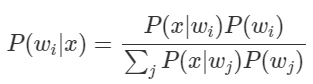
좌변은 우리가 구하고자 하는 Posterior이고, 우변의 분자는 Likelihood와 Prior의 곱이며, 우변의 분모는 Evidence라고 보통 부르는데, 이 또한 Likelihood와 Prior들을 통해 구할 수 있다.

$w$ 파라미터에 따른 $x$ 클래스라고 한다면, 클래스를 알때 최적의 파라미터를 구할 수 있다.

Posterior( $P(w_i|x)$ ): 피부 밝기( $w$ )가 주어졌을 때 그 물고기가 농어일 확률 또는 연어일 확률. 즉 단서가 주어졌을 때, 대상이 특정 클래스에 속할 확률. 우리가 최종적으로 구해야 하는 값이다.
Likelihood( $P(x|w_i)$ ): 농어 또는 연어의 피부 밝기($ $x$ ) 가 어느 정도로 분포되어 있는지의 정보. 즉 각 클래스에서 우리가 활용할 단서가 어떤 형태로 분포 돼 있는지를 알려준다. Posterior를 구하는 데 있어서 매우 중요한 단서가 된다.
Prior( $P(w_i)$ ): 피부 밝기( $x$ )에 관계 없이 농어와 연어의 비율이 얼마나 되는지의 값. 보통 사전 정보로 주어지거나, 주어지지 않는다면 연구자의 사전 지식을 통해 정해줘야 하는 값이다.

Likelihood, 우도

주어진 파라미터 세트가 특정 데이터를 얻을 가능성을 측정한다. 좀 더 구체적으로 말하면, 우도는 관측된 데이터가 어떤 통계적 모델의 특정 파라미터 값에 대해 얼마나 "가능성이 높은지"를 나타내는 값이다.

우도는 조건부 확률의 개념을 활용하여 정의된다. 그렇다면 조건부확률 vs likelihood 비교를 통해 likelihood가 뭔지 알아보자.

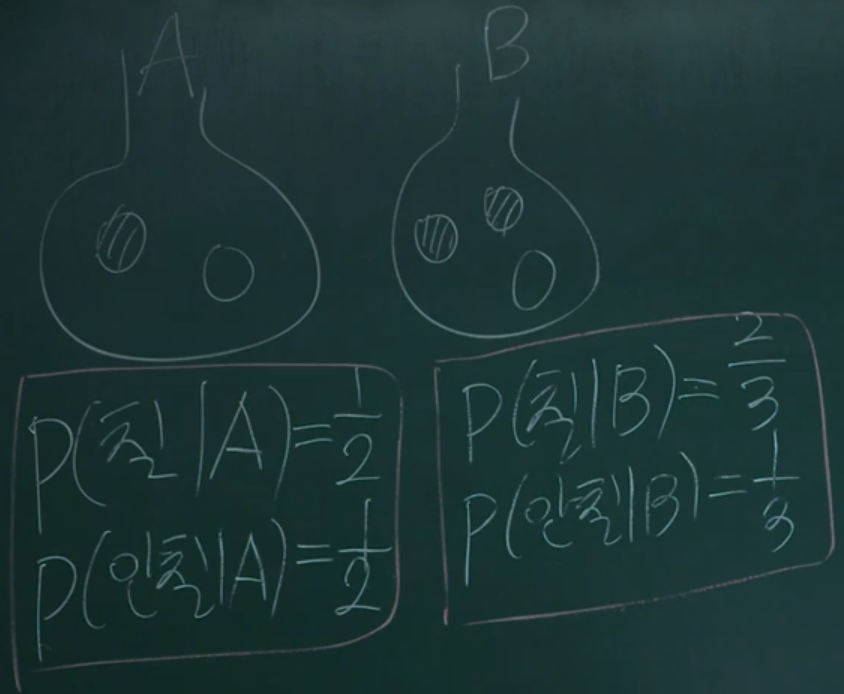
각 주머니를 선택하였을때 칠한 공, 안칠한 공을 선택할 조건부확률을 구할 수 있다. 각 주머지를 기준으로 조건부확률의 합은 1이고 확률 분포를 나타낸다. 그렇다면 likelihood는 칠한 공을 선택했을 때, A or B 둘 중 어디서 나왔을까를 나타낸다. 관측된 데이터가, 어떤 사건에서부터 "발생할 가능성이 높은지"를 나타내는 것입니다.

그림에서 조건부는 세로 방향, likelihood는 가로 방향으로 볼 수 있다.

전체 표본집합의 결합확률밀도 함수를 likelihood function이라고 한다.

++
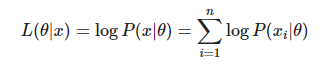
챗지피한테도 물어봤다.
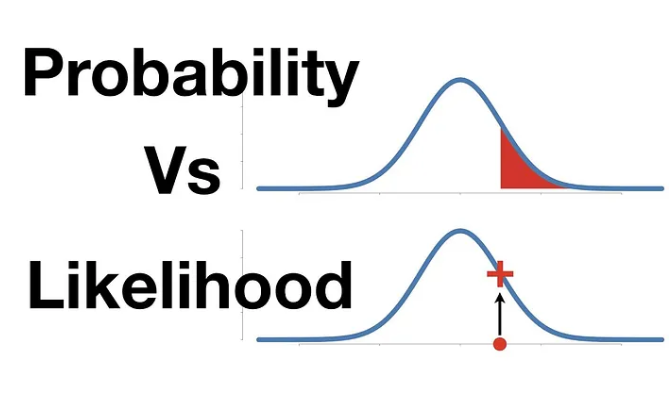
Likelihood vs. Probability

Probability measures the chance of a particular outcome or set of outcomes occurring in the future, given a specific model or assumption.
Likelihood is about measuring the plausibility of different models given the data that has already occurred. It asks, "Given this data, how plausible are these parameters?"

MLE

그러면 자연스럽게 의문이 든다. 어떤 주머니에서 나왔을까? x가 대체 뭐였길래 measurement가 이렇게 나왔을까?에 대한 답을 하고 싶어진다.

예를 들어보자

$z_1=x+n_1, z_2=x+n_2, n~N(0,\sigma^2)$ 에 대해서

likelihood는 $p(z_1, z_2|x)=p(z_1|x)p(z_2|x)$ (독립 시행 가정)

$p(z_1|x)=\frac{1}{\sqrt{\pi\sigma^2}}\exp(-\frac{(z_1-x)^2}{2\sigma^2})$ 이며 $z_2$ 도 동일하다.

두 확률을 곱하여 값을 구하고 log를 취한다. 이후 미분하여 $x$ 에 대해서 미분하여 0이되는 값을 찾는다.

미분해서 기울기가 0일 경우 최대값을 가질 것이다라고 가정하여, 값을 구할 수 있다. 여기서 두 확률 분포를 곱하는 것은 두 확률 분포의 likelihood를 최대화하는 문제로 풀었기 때문이다. 그리고 x를 추정하는 이유는 가장 최대가 되도록 하는 x를 찾고자하기 때문이다.

++
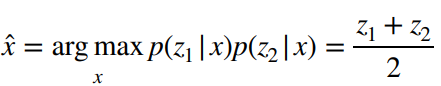
앞선 수식에서 $-log$ 를 취하면 MSE(mean square error)와 같아진다. 이 상황에서 MLE로 구하면 Least squares solution (최소자승법, 최소제곱법)과 일치한다. 여기서도 미분값이 0이 되는 지점을 예측한다.

다른 예를 들어보자
"실제 몸무게(t)는 내가 예측한 몸무게(y)를 평균으로 하고 특정 값 $\sigma$ 를 표준편차로 하는 Gaussian Distribution을 따른다" 고 할 수 있고, 다음과 같이 쓸 수 있다.

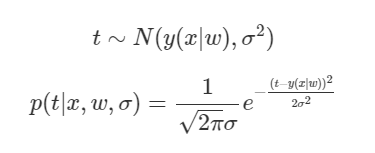
여기서 $sigma$ 는 무엇을 의미할까? 우리가 Gaussian Distribution을 이용하는 이유는 자신이 한 예측을 100% 확신할 수 없기 때문이라고 했다.

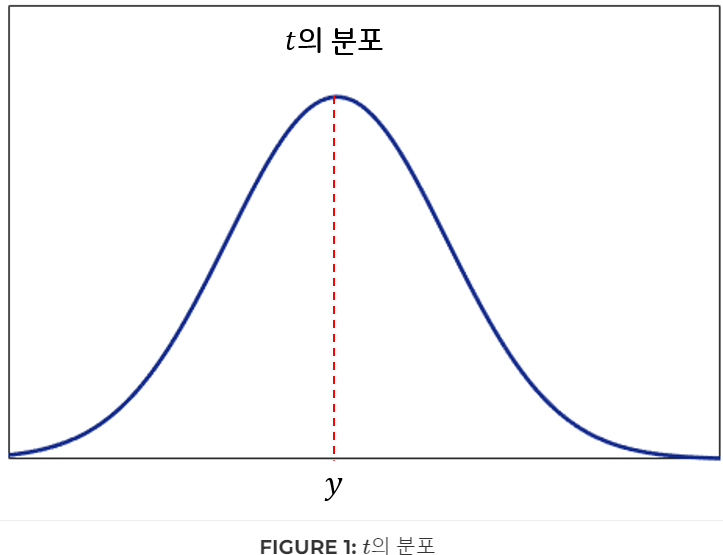
그래서 그림1과 같은 형태로 대답하게 된 것인데, 그림1에서 Distribution의 폭이 작다는 것 ( $\sigma$ 가 작다는 것)은 무엇을 의미할까? 바로 우리가 예측한 값에 더 확신한다는 뜻이다. 반대로 폭이 크다는 것( $\sigma$ 가 크다는 것)은 그 만큼 우리가 예측한 값에 자신이 없다는 뜻이다. 즉, $\sigma$ 는 우리가 한 예측이 얼마나 불확실한지의 정도 를 나타낸다. 하지만 $\sigma$ 는 우리의 예측 능력에 따른 변수가 아니다. 우리가 풀려는 문제의 특성에 따라 설정되는 값이다. 우리가 풀려는 문제가 각 $x$ 에 대해서 $t$ 값이 대부분 하나로 일정하게 나오는 문제라면 $\sigma$ 는 작을 것이고, $x$ 가 같더라도 다양한 $t$ 가 나올 수 있는 문제라면 $\sigma$ 는 클것이다. 즉 우리가 문제의 특성을 파악하고 설정해주는 상수 값이다.

다시 말하면 $p(D|w)$ 가 가장 높다고 대답하는 모델, 즉 $p(D|w)$ 가 최대가 되는 모델이어야 한다. 결국 우리가 해야 할 일은 $p(D|w)$ 가 최대가 되는 $w$ 를 찾는 것이고, 여기서 $p(D|w)$ 가 바로 likelihood기 때문에 이 방식의 이름이 Maximum Likelihood Estimation이다.

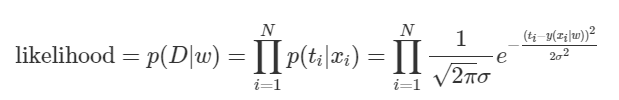
이런 문제에서 우리는 주로 $log$ 를 취해 준다. 먼저 likelihood가 최대면 likelihood의 log값도 최대기 때문에 log를 취해줘도 문제가 발생하지 않고, 또한 복잡한 곱셈 연산을 덧셈 연산으로 바꿔주기 때문에 수식의 전개가 용이하다.

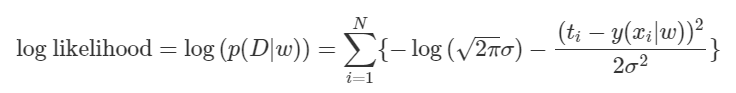
위의 상수 값들을 모두 제거해주고 앞의 부호를 바꿔주어 maximize 대신 minimize하기로 하면 다음 식이 남게 된다.

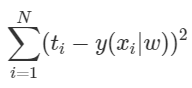
예측값과 실제 값의 차이의 제곱. L2 Loss이다. 일반적으로 Deep Learning에서 Regression 시에 가장 많이 쓰는 Loss 함수가 튀어나왔다. 이렇게 MLE를 이용하면 Regression에서 L2 Loss를 쓰는 이유를 증명해 낼 수 있다. 반대로, 우리가 앞으로 Deep Learning 등에서 L2 Loss를 이용한다는 것은 주어진 Data로부터 얻은 Likelihood를 최대화시키겠다는 뜻으로 해석할 수 있다. L2 Loss를 최소화 시키는 일은 Likelihood를 최대화 시키는 일인 것이다. 참고로 Classification 문제에서는 Bernoulli Distribution을 이용하면 비슷한 방법으로 Cross Entropy Error를 유도할 수 있다.

이러한 고민이 왜 필요할까? 딥러닝 관점에서 보면

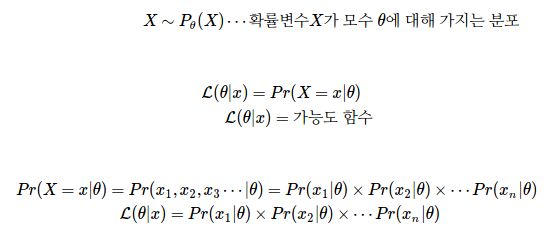
파라미터 세타에 대해서 데이터가 주어졌을때 분포가 데이터를 얼마나 잘 설명하는가 (=머신러닝의 미션!) 이고 이를 Maximize해여 모델이 데이터를 이해하고 특정 클래스에 대해잘 예측할 수 있다.

3개의 모델을 구현했고, 모델의 마지막 softmax layer에서 확률 값을 뽑아보았다. 이 모델 중에서 어떤 모델이 가장 정답에 가까운 distribution 인가?

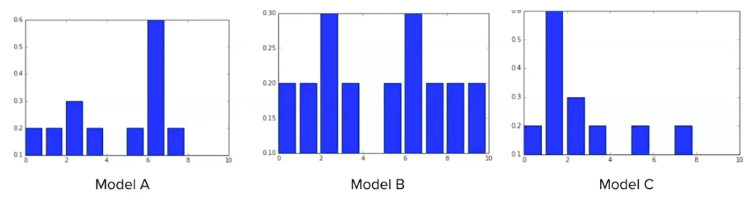
모델 c가 데이터를 가장 잘 설명하는 distribution 이라고 말할 수 있다. 즉, likelihood가 가장 높은 분포이다.

어떤 클래스로 예측을 하고 싶은데, 우리 모델이 정답 클래스로 예측했을때, 정답값일때의 조건부 확률값의 곱이 곧 가능도이다. 다른 클래스로 예측한 조건부 확률값은 궁금하지 않다.

Maximum A Posterior (MAP)

likelihood 뿐만 아니라 prior distribution까지 고려한 posterior를 maximize하자는 것!

MAP는 베이지안 룰에 의해 사전확률을 사용한 사후 확률 최대화 문제로 풀 수 있다.

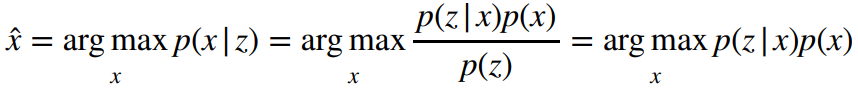
이전의 MLE와 다른 점은 $p(x)$ 를 곱해준 것이다. 곱해주려면 x의 분포를 사전에 알고 있어야 한다. => 사전 정보를 제공해 주는 것이므로 prior distribution 이라고 한다.

정리하면 likelihood 뿐만 아니라, prior distribution 을 고려하여 posterior를 maximize하는 것이다.

예를 들어보자.

$z_1=x+n_1, z_2=x+n_2, n~N(0,\sigma^2)$ 에 대해서

Likelihood는 $p(z_1, z_2|x)=p(z_1|x)p(z_2|x)p(x)$ (독립 시행 가정) 이고

$p(z_1|x)=\frac{1}{\sqrt{\pi\sigma^2}}\exp(-\frac{(z_1-x)^2}{2\sigma^2})$ 이며 $z_2$ 도 동일하다.

Likelihood와 달라진 점은 $p(x)$ 를 곱해주는 부분이다.

다른 예를 들어보자.
$w$ 에 Prior를 걸어주자. $w$ 에 0을 평균으로 하는 Gaussian Distribution이라는 Prior를 걸어주게 되면, $w$ 는 자연스럽게 0주변에 배치 될 것이다.

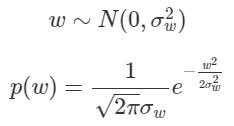
먼저 likelihood에서와 같이 Posterior에 log를 취해주자. 그리고 그 값을 최대로 하는 $w$ 를 찾는 것이 우리의 목표이다.

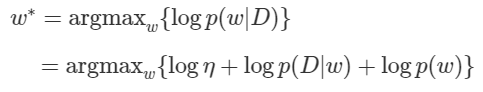
여기서 $log\space p(D|w)$ 는 Likelihood 이므로 이 값을 Maximize하는 것은 위에서 봤듯이

$\sum_{i}^{N}(t_i-y(x_i|w)^2)$ 를 Minimize 하는 것과 같다. $L(w)=\sum_{i}^{N}(t_i-y(x_i|w)^2)$ 라고 치환하여 대입하면 다음과 같다.

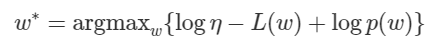
이제 $logp(w)$ 식을 대입하면 다음과 같게 된다.

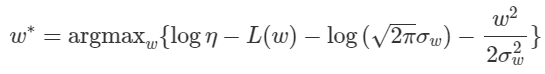
여기서 $\eta, \pi, \sigma_w$ 는 전부 상수이므로 관련된 term들을 제거해주면 다음 식을 minimize하는 문제가 된다.

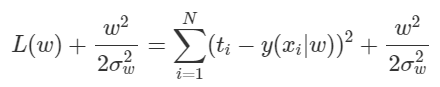
$\frac{1}{2\sigma_{w}^2}$ 는 상수이므로 $\alpha$ 등으로 치환하면 Weight Decay(L2 Regularization) 방식을 적용한 Deep Learning의 Loss함수가 된다. 우리는 Gaussian Distribution을 Prior로 준 문제의 MAP로 부터 Weight Decay식을 유도해냈다. 또한 우리가 앞으로 Deep Learning 등에서 Weight Decay, 그 중에서도 L2 Regularization을 쓴다는 것은 주어진 Data를 적용함과 동시에 w에 Gaussian Distribution이라는 Prior를 걸어 주어 MAP를 통해 $w$ 를 구하겠다는 것으로 해석할 수 있다. L2 Regularization을 적용하는 일은 $w$ 에 Gaussian Distribution을 Prior로 걸어 주는 일인 것이다. 참고로 Laplacian Distribution을 Prior로 걸어 주면 L1 Regularization을 얻을 수 있다. 직접 해보기 어렵지 않을 것이다.

MLE와 연관지어서 다시 생각해보자.

MLE는 "데이터가 주어졌을때 분포가 데이터를 얼마나 잘 설명하는가" 이다. MLE는 모델의 파라미터가 데이터를 생성하는데 얼마나 효과적인지만 고려하며, 파라미터 자체에 대한 사전 지식은 고려하지 않는다.

MAP는 "데이터가 주어졌을때 분포와 사전 확률 분포가 데이터를 얼마나 잘 설명하는가" 이다.

참고자료
https://hyeongminlee.github.io/post/bnn001_bayes_rule/

https://angeloyeo.github.io/2020/07/17/MLE.html

https://velog.io/@cha-suyeon/DL-%EC%86%90%EC%8B%A4-%ED%95%A8%EC%88%98loss-function-%EC%A0%95%EC%9D%98

https://ko.wikipedia.org/wiki/%EC%A0%84%EC%B2%B4_%ED%99%95%EB%A5%A0%EC%9D%98_%EB%B2%95%EC%B9%99#:~:text=%EC%A0%84%EC%B2%B4%20%ED%99%95%EB%A5%A0%EC%9D%98%20%EB%B2%95%EC%B9%99(%E5%85%A8%E9%AB%94,%ED%99%95%EB%A5%A0%20%EC%A0%95%EB%A6%AC%20%EA%B3%B5%EC%8B%9D%EC%9D%B4%20%EB%93%A4%EC%96%B4%EA%B0%84%EB%8B%A4.

함지율

꿈 꾸는 디그다

이전 포스트