BOJ 15657 (N과 M (8))

• 문제
  N개의 자연수와 자연수 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오. N개의 자연수는 모두 다른 수이다.
  
  N개의 자연수 중에서 M개를 고른 수열

  • 같은 수를 여러 번 골라도 된다.
  • 고른 수열은 비내림차순이어야 한다.
  • 길이가 K인 수열 A가 A1 ≤ A2 ≤ ... ≤ AK-1 ≤ AK
    를 만족하면, 비내림차순이라고 한다.

• 입력
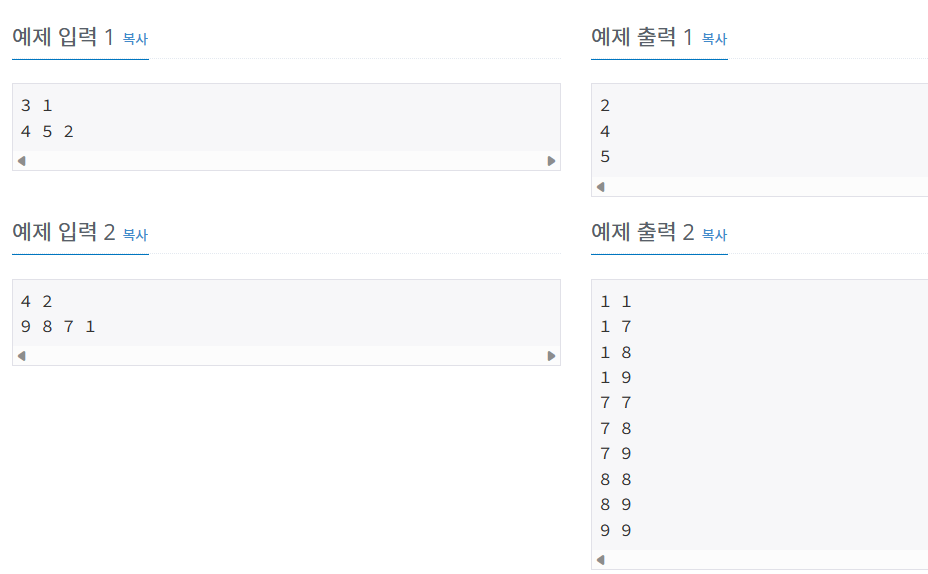
  첫째 줄에 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)
  둘째 줄에 N개의 수가 주어진다. 입력으로 주어지는 수는 10,000보다 작거나 같은 자연수이다.
  
  
• 출력
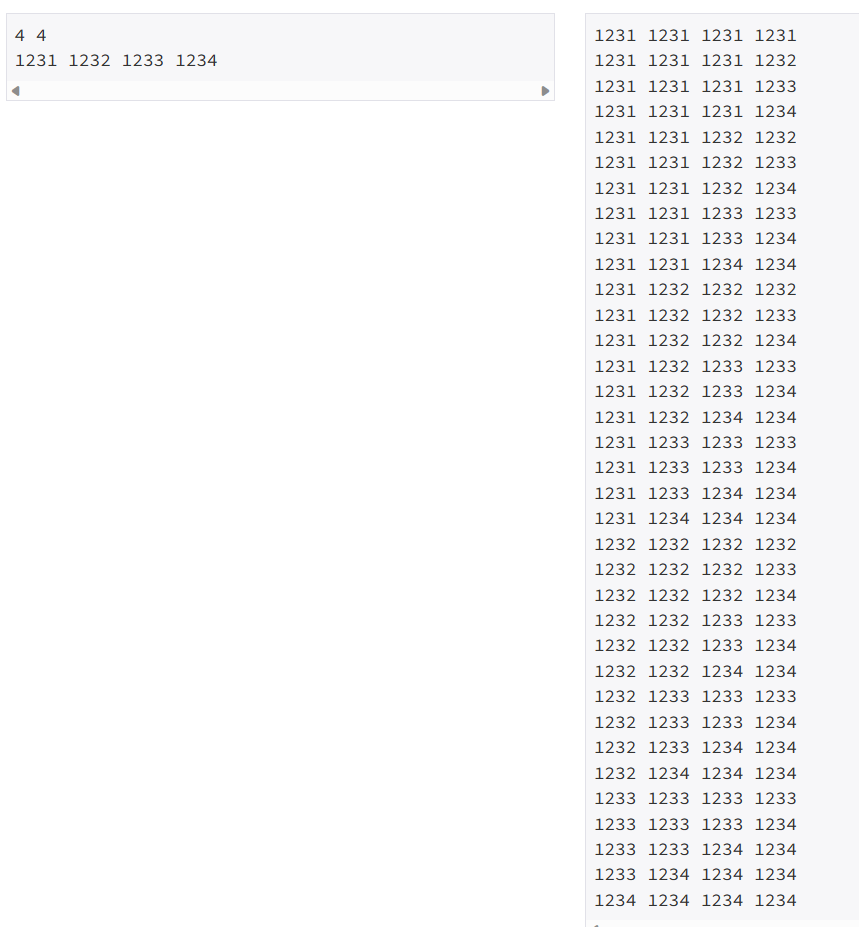
  한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다.
  
  수열은 사전 순으로 증가하는 순서로 출력해야 한다.

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int N, M;
int numbers[8];
vector<int> answer;

void fast_io() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
}

void input() {
	cin >> N >> M;
	for (int i = 0; i < N; i++)
		cin >> numbers[i];
}

void dfs(int depth) {
	answer.push_back(depth);
	if (answer.size() == M) {
		for (int i = 0; i < M; i++) {
			cout << answer[i] << ' ';
		}
		cout << '\n';
        /*출력 후 맨 끝에 있는 수 빼버리기*/
		answer.pop_back();
		return;
	}
	for (int i = 0; i < N; i++) {
		if (answer[answer.size() - 1] > numbers[i])
			continue;
		dfs(numbers[i]);
	}
    /*해당 숫자에 대하여 모든 깊이까지 탐색 후 벡터 비워주기*/
	answer.pop_back();
}

int main() {
	fast_io();
	input();
    /* 정렬을 해주면 문제를 쉽게 풀 수 있다 */
	sort(numbers, numbers + N);
	for (int i = 0; i < N; i++)
	{
		dfs(numbers[i]);
	}
	return 0;
}

   N과 M 문제의 8번째 시리즈 문제이다. 이 시리즈는 입력의 크기를 8로 제한하여 완전탐색(Brute-Force) 방식으로 문제를 풀 수 있도록 만든 문제같다.

중복을 허락하여 N개중 M개를 고르는 순열을 만들때 조건으로 고른 수열이 비 내림차순이 되도록 하는 조건이 달려있다.
-> 다음에 올 수가 맨 끝에 올 수보다 크거나 같아야 한다.

이를 쉽게 푸려면 우선 숫자를 담은 데이터를 정렬 후 담을 수의 맨 끝수와 다음에 들어올 수를 비교하기만 해주면 이전 N과 M 문제와 크게 다른 부분은 없는 것 같다.

시간 복잡도 : O(N^M)

숏코딩

#include <iostream>
#include <algorithm>
using namespace std;
int n,m;
int b[9],a[9]={0,};
void dfs(int idx,int len) 
{
	if(len==m) 
	{
		for(int i=0;i<m;i++) cout<<a[i]<<' '; 
		cout<<'\n';
		return;
	}
	for(int i=idx;i<n;i++) 
	{
		a[len]=b[i];
		dfs(i,len+1);
	}
}
int main()
{
	cin>>n>>m;
	for(int i=0;i<n;i++) cin>>b[i];
	sort(b,b+n);
	dfs(0,0);
}

   index와 길이 정보를 같이 줘서 정렬을 했으므로 해당 숫자가 포함된 index 부터 넣고 재귀 함수를 호출하도록 짠 코드 같다.

내 풀이는 0번 index부터 비교를 하기때문에(정렬의 의미가 퇴색) 숏코딩에 담긴 방식이 조금 더 효율적으로 동작할 것 같다.