BOJ 1934 (최소공배수)

• 문제
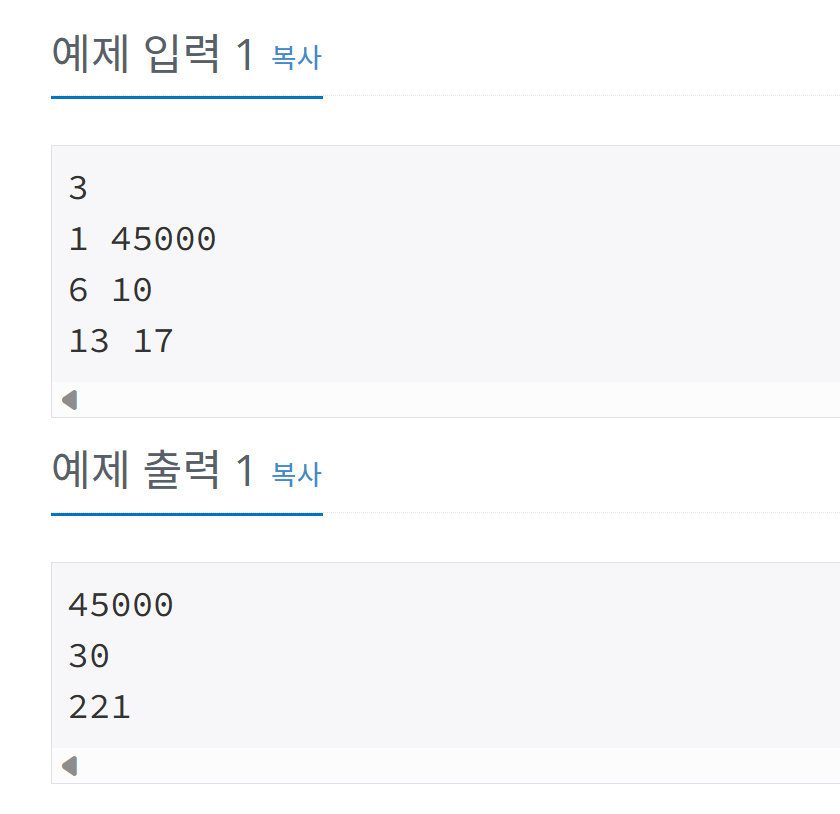
  두 자연수 A와 B에 대해서, A의 배수이면서 B의 배수인 자연수를 A와 B의 공배수라고 한다. 이런 공배수 중에서 가장 작은 수를 최소공배수라고 한다. 예를 들어, 6과 15의 공배수는 30, 60, 90등이 있으며, 최소 공배수는 30이다.
  
  두 자연수 A와 B가 주어졌을 때, A와 B의 최소공배수를 구하는 프로그램을 작성하시오.
  
  
• 입력
  첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 1,000)가 주어진다. 둘째 줄부터 T개의 줄에 걸쳐서 A와 B가 주어진다. (1 ≤ A, B ≤ 45,000)
  
  
• 출력
  첫째 줄부터 T개의 줄에 A와 B의 최소공배수를 입력받은 순서대로 한 줄에 하나씩 출력한다.

#include<iostream>
using namespace std;
int T;
int A, B;
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
}

int GCD(int x, int y)
{
	if (y == 0)
		return x;
	else if (y == 1)
		return 1;
	else
		return GCD(y, x % y);
}

int main()
{
	fast_io();
	cin >> T;
	while (T--)
	{
		cin >> A >> B;
		int temp = GCD(A, B);
		cout << (A * B) / temp << '\n';
	}
	return 0;
}

   최소공배수 -> 두 수의 곱 / 최대공약수를 하면 된다. 유클리드 호제법을 이용하여 최대공약수를 구해주면 된다.

최대공약수를 구하는 법
1. (3항 연산자 이용)

int gcd(int a, int b)
{
	return b ? gcd(b, a%b) : a;
}

2. 반복문 이용

int gcd(int a, int b)
{
    int c;
	while(b)
	{
		c = a % b;
		a = b;
		b = c;
	}
    return a;
}

3. 풀이에 적은 방식처럼 재귀 이용

* 다른 분들의 숏코딩을 보니 <bits/stdc++.h> (gcc계열에는 내장된) 헤더 파일을 많이들 쓰신다.
-> GNU C++의 표준 라이브러리 헤더가 아니다
-> #include의 귀찮음을 덜어주지만 단점도 있음 (컴파일시 시간이 더 걸릴 듯)

C++17 버전부터 numeric 헤더에 gcd, lcm 함수가 추가되어 바로 구할 수 있다.