문제
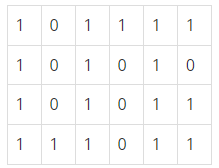
N×M크기의 배열로 표현되는 미로가 있다.
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.
- 입력
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.- 출력
첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.
#include<iostream>
#include<string>
#include<queue>
using namespace std;
int arr[101][101]; //판 입력
bool visited[101][101]; //방문 여부 확인
int dist[101][101]; //거리 측정 용
int dy[4] = { -1,1,0,0 };
int dx[4] = { 0,0,-1,1 };
int N, M;
void fast_io()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
}
void bfs(int num1, int num2)
{
queue<pair<int, int>> q;
q.push(make_pair(num1, num2));
visited[num1][num2] = true;
while (!q.empty())
{
int y = q.front().first;
int x = q.front().second;
q.pop();
for (int i = 0; i < 4; i++)
{
int ny = y + dy[i];
int nx = x + dx[i];
if (ny >= 0 && ny < N && nx >= 0 && nx < M && !visited[ny][nx] && arr[ny][nx] == 1)
{
visited[ny][nx] = true;
q.push(make_pair(ny, nx));
dist[ny][nx] = dist[y][x] + 1;
}
}
}
}
int main()
{
void fast_io();
cin >> N >> M;
for (int i = 0; i < N; i++)
{
string s; cin >> s;
for (int j = 0; j < M; j++)
{
arr[i][j] = s[j] - '0';
}
}
bfs(0, 0);
cout << dist[N - 1][M - 1] + 1;
}BFS는 최단거리를 보장하기 때문에 BFS를 이용하여 N,M까지의 이동 과정중 거리를 배열에 같이 저장해주면 원하는 기대 출력 값을 얻을 수 있다.