BOJ 11403 (경로 찾기)

• 문제
  가중치 없는 방향 그래프 G가 주어졌을 때, 모든 정점 (i, j)에 대해서, i에서 j로 가는 경로가 있는지 없는지 구하는 프로그램을 작성하시오.
  
  
• 입력
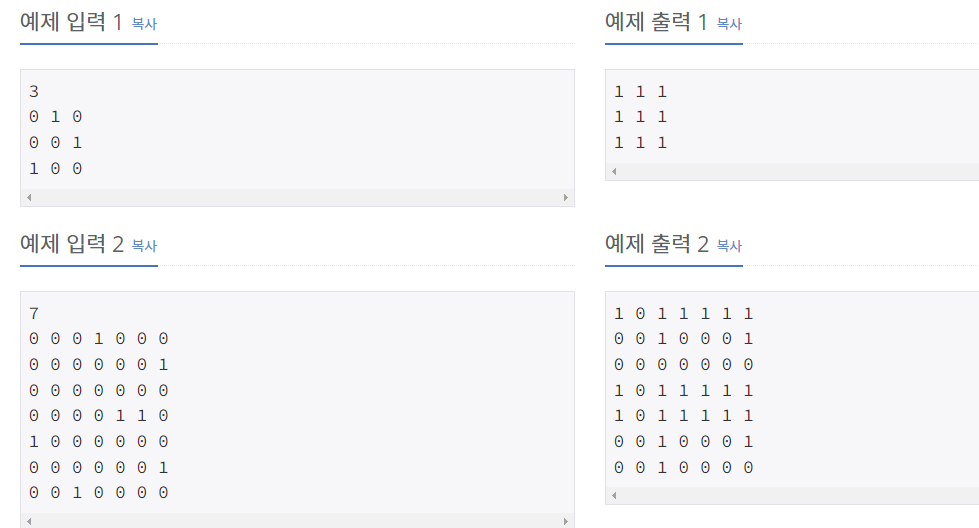
  첫째 줄에 정점의 개수 N (1 ≤ N ≤ 100)이 주어진다. 둘째 줄부터 N개 줄에는 그래프의 인접 행렬이 주어진다. i번째 줄의 j번째 숫자가 1인 경우에는 i에서 j로 가는 간선이 존재한다는 뜻이고, 0인 경우는 없다는 뜻이다. i번째 줄의 i번째 숫자는 항상 0이다.
  
  
• 출력
  총 N개의 줄에 걸쳐서 문제의 정답을 인접행렬 형식으로 출력한다. 정점 i에서 j로 가는 경로가 있으면 i번째 줄의 j번째 숫자를 1로, 없으면 0으로 출력해야 한다.

#include<iostream>

using namespace std;
int arr[101][101];
int N;
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
}
//3중반복문으로 구현 가능 (중간 다리 역할이 가장 바깥 반복문인 것에 주의)
void floyd()
{
	for (int middle = 0; middle < N; middle++)
	{
		for (int from = 0; from < N; from++)
		{
			for (int to = 0; to < N; to++)
			{
				if (arr[from][middle] && arr[middle][to])
				{
					arr[from][to] = 1;
				}
			}
		}
	}
}

int main()
{
	void fast_io();
	cin >> N;
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			int num; cin >> num;
			arr[i][j] = num;
		}
	}
	floyd();
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			cout << arr[i][j] << ' ';
		}
		cout << '\n';
	}
}

  플로이드-워셜 기법을 이용하는 문제풀이다. 플로이드 워셜 기법은 그래프에서 가능한 모든 노드 쌍에 대해 최단거리를 구하는 알고리즘인데 처음 접해보는 알고리즘 기법이었다. (3중첩 반복문을 사용하며 중간 다리 역할을 하는 노드를 가장 바깥쪽 반복문에 둔다.)

다른 최단 거리 구하는 문제로 더 친숙해 져야겠다.

시간 복잡도 : O(N^3)