BOJ 2193 (이친수)

• 문제
  0과 1로만 이루어진 수를 이진수라 한다. 이러한 이진수 중 특별한 성질을 갖는 것들이 있는데, 이들을 이친수(pinary number)라 한다. 이친수는 다음의 성질을 만족한다.
  

1. 이친수는 0으로 시작하지 않는다.
2. 이친수에서는 1이 두 번 연속으로 나타나지 않는다. 즉, 11을 부분 문자열로 갖지 않는다.
   
   예를 들면 1, 10, 100, 101, 1000, 1001 등이 이친수가 된다. 하지만 0010101이나 101101은 각각 1, 2번 규칙에 위배되므로 이친수가 아니다.
   
   N(1 ≤ N ≤ 90)이 주어졌을 때, N자리 이친수의 개수를 구하는 프로그램을 작성하시오.
   
   

• 입력
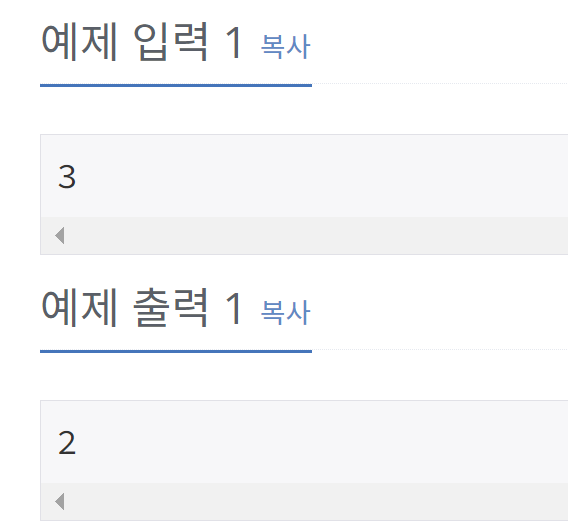
  첫째 줄에 N이 주어진다.
  
  
• 출력
  첫째 줄에 N자리 이친수의 개수를 출력한다.

#include<iostream>
using namespace std;
int N;
long long arr[91];
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
}

int main()
{
	fast_io();
	cin >> N;
	arr[1] = 1;
	arr[2] = 1;
	for (int i = 3; i <= N; i++)
	{
		arr[i] = arr[i - 2] + arr[i - 1];
	}
	cout << arr[N];
}

  맨 끝이 0으로 끝나면 다음 숫자에서 2개가 추가될 수 있고 1로 끝나면 1개만 추가될 수 있다.
N이 1일때 '1'으로 1개, N이 2일때 '10'으로 1개, N이 3일때 '100,101'으로 2개가 나온다. 이어서 N은 5까지 해본 결과 피보나치 수열과 같은 점화식이 나오는 것을 확인할 수 있었다.     "arr[N]=arr[N-1]+arr[N-2]"

  맨 앞이 1로 시작해야하니 N=2부터는 앞에 두 숫자가 10으로 고정된다.
N일때 고정된 앞 2자리를 제거하면 N-1일때 맨앞 1을 제거한 숫자, N-2일때 숫자가 나오므로 위와 같은 결과가 나오는듯 하다.

맨 처음엔 점화식을 찾고 재귀함수로 구현했으나 당연히 시간초과 + 배열에 저장하는 선형 시간 알고리즘으로 바꿨으나 자료형 생각을 깊게 하지 않아 또 틀렸었다.

시간 복잡도 : O(N)