- 문제
n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다.
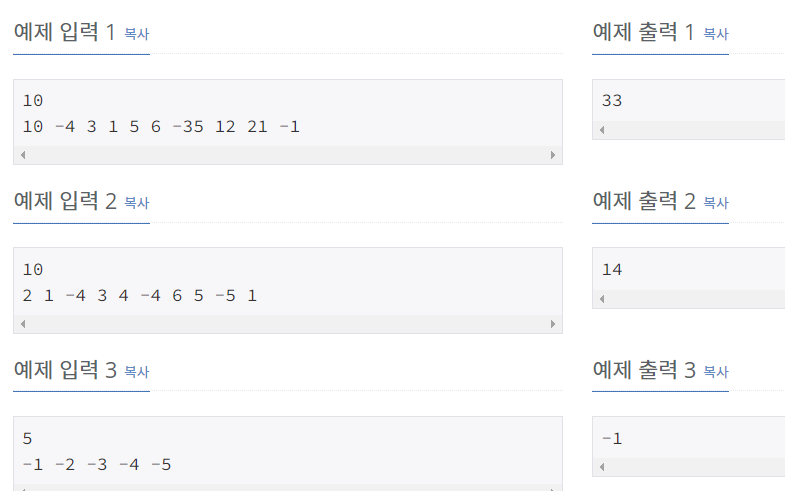
예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.- 입력
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.- 출력
첫째 줄에 답을 출력한다.
#include<iostream>
#include<algorithm>
using namespace std;
int N;
int arr[100001];
int dp[100001];
void fast_io()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
}
int main()
{
fast_io();
cin >> N;
for (int i = 1; i <= N; i++)
{
int num; cin >> num;
arr[i] = num;
}
int result = arr[1]; dp[1] = arr[1];
for (int i = 2; i <= N; i++)
{
dp[i] = max(dp[i - 1] + arr[i], arr[i]);
result = max(result, dp[i]);
}
cout << result;
}문제의 조건을 보니 시간복잡도 O(N)으로 풀어야하고 Dynamic Programming 기법을 사용해야 하는것을 캐치할 수 있었다.