BOJ 24265~24267, 24313 (단계별 풀이 : 시간복잡도 (2))

• 24265번

  MenOfPassion 알고리즘은 다음과 같다.
  
  MenOfPassion(A[], n) {
  sum <- 0;
  for i <- 1 to n - 1
  for j <- i + 1 to n
  sum <- sum + A[i] × A[j]; // => 코드1
  return sum;
  }
  
  
• 입력
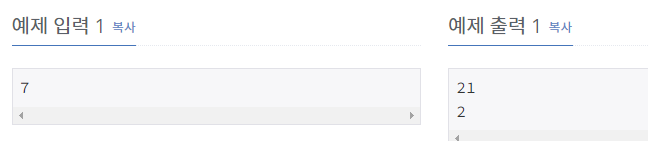
  첫째 줄에 입력의 크기 n(1 ≤ n ≤ 500,000)이 주어진다.
  
  
• 출력
  첫째 줄에 코드1 의 수행 횟수를 출력한다.
  
  둘째 줄에 코드1의 수행 횟수를 다항식으로 나타내었을 때, 최고차항의 차수를 출력한다. 단, 다항식으로 나타낼 수 없거나 최고차항의 차수가 3보다 크면 4를 출력한다.
  

#include<iostream>
using namespace std;
long long N;
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
}
int main()
{
	fast_io();
	cin >> N;
	cout << N*(N-1)/2 << '\n' << 2;
}

n에 대하여 반복문이 2번 돌아가므로 시간복잡도는 O(N^2)을 갖고 n개 중 2개의 수를 고르는 것과 같은 식이 나온다.

• 24266번

  MenOfPassion 알고리즘은 다음과 같다.
  
  MenOfPassion(A[], n) {
  sum <- 0;
  for i <- 1 to n
  for j <- 1 to n
  for k <- 1 to n
  sum <- sum + A[i] × A[j] × A[k]; // => 코드1
  return sum;
  }
  
  
• 입력
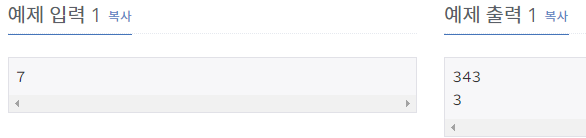
  첫째 줄에 입력의 크기 n(1 ≤ n ≤ 500,000)이 주어진다.
  
  
• 출력
  첫째 줄에 코드1 의 수행 횟수를 출력한다.
  
  둘째 줄에 코드1의 수행 횟수를 다항식으로 나타내었을 때, 최고차항의 차수를 출력한다. 단, 다항식으로 나타낼 수 없거나 최고차항의 차수가 3보다 크면 4를 출력한다.
  

#include<iostream>
using namespace std;
long long N;
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
}
int main()
{
	fast_io();
	cin >> N;
	cout << N*N*N << '\n' << 3;
}

n에 대하여 3중첩 반목문이 돌아가기 때문에 시간복잡도는 O(N^3)이 된다.

• 24267번

  MenOfPassion 알고리즘은 다음과 같다.
  
  MenOfPassion(A[], n) {
  sum <- 0;
  for i <- 1 to n - 2
  for j <- i + 1 to n - 1
  for k <- j + 1 to n
  sum <- sum + A[i] × A[j] × A[k]; # 코드1
  return sum;
  }
  
  
• 입력
  첫째 줄에 입력의 크기 n(1 ≤ n ≤ 500,000)이 주어진다.
  
  
• 출력
  첫째 줄에 코드1 의 수행 횟수를 출력한다.
  
  둘째 줄에 코드1의 수행 횟수를 다항식으로 나타내었을 때, 최고차항의 차수를 출력한다. 단, 다항식으로 나타낼 수 없거나 최고차항의 차수가 3보다 크면 4를 출력한다.
  

#include<iostream>
using namespace std;
long long N;
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
}
int main()
{
	fast_io();
	cin >> N;
	cout << N*(N-1)*(N-2)/6 << '\n' << 3;
}

n에 대하여 3중첩 반복문이 돌아가기에 시간복잡도는 O(N^3)이 된다. n개의 수 중 3개의 숫자를 고르는 것과 같은 식이 나온다.

• 24313번

• 문제
  오늘도 서준이는 점근적 표기 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자.
  
  알고리즘의 소요 시간을 나타내는 O-표기법(빅-오)을 다음과 같이 정의하자.
  
  O(g(n)) = {f(n) | 모든 n ≥ n0에 대하여 f(n) ≤ c × g(n)인 양의 상수 c와 n0가 존재한다}
  * 이 정의는 실제 O-표기법(https://en.wikipedia.org/wiki/Big_O_notation)과 다를 수 있다.
  
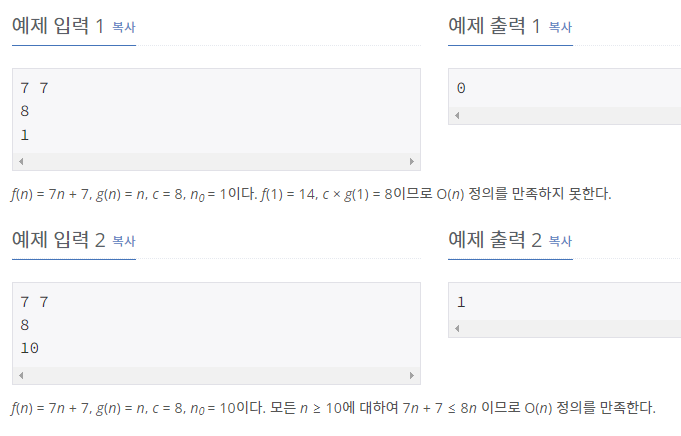
  함수 f(n) = a1n + a0, 양의 정수 c, n0가 주어질 경우 O(n) 정의를 만족하는지 알아보자.
  
  
• 입력
  첫째 줄에 함수 f(n)을 나타내는 정수 a1, a0가 주어진다. (0 ≤ |ai| ≤ 100)
  다음 줄에 양의 정수 c가 주어진다. (1 ≤ c ≤ 100)
  다음 줄에 양의 정수 n0가 주어진다. (1 ≤ n0 ≤ 100)
  
  
• 출력
  f(n), c, n0가 O(n) 정의를 만족하면 1, 아니면 0을 출력한다.
  

#include<iostream>
using namespace std;
int a0, a1;
int c, n0;
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
}
int main()
{
	fast_io();
	cin >> a1 >> a0 >> c >> n0;
	if (a1 * n0 + a0 <= c * n0 && c >= a1)
	{
		cout << 1;
	}
	else
	{
		cout << 0;
	}
}

문제를 보면 if문에서 첫번째 조건만 만족하면 된다고 생각할 수 있지만 문제에서 빅O의 조건 중 a0가 음수인 경우에 모든 n>=n0에 대하여를 만족하려면 c>=a1 조건까지 참이어야 한다.