BOJ 2563 (색종이)

• 문제
  가로, 세로의 크기가 각각 100인 정사각형 모양의 흰색 도화지가 있다. 이 도화지 위에 가로, 세로의 크기가 각각 10인 정사각형 모양의 검은색 색종이를 색종이의 변과 도화지의 변이 평행하도록 붙인다. 이러한 방식으로 색종이를 한 장 또는 여러 장 붙인 후 색종이가 붙은 검은 영역의 넓이를 구하는 프로그램을 작성하시오.
  
  
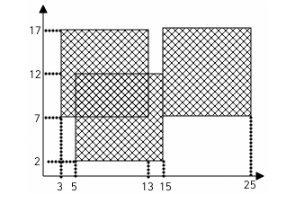
  예를 들어 흰색 도화지 위에 세 장의 검은색 색종이를 그림과 같은 모양으로 붙였다면 검은색 영역의 넓이는 260이 된다.
  
  
• 입력
  첫째 줄에 색종이의 수가 주어진다. 이어 둘째 줄부터 한 줄에 하나씩 색종이를 붙인 위치가 주어진다. 색종이를 붙인 위치는 두 개의 자연수로 주어지는데 첫 번째 자연수는 색종이의 왼쪽 변과 도화지의 왼쪽 변 사이의 거리이고, 두 번째 자연수는 색종이의 아래쪽 변과 도화지의 아래쪽 변 사이의 거리이다. 색종이의 수는 100 이하이며, 색종이가 도화지 밖으로 나가는 경우는 없다
  
  
• 출력
  첫째 줄에 색종이가 붙은 검은 영역의 넓이를 출력한다.

#include<iostream>
using namespace std;

int paper[101][101];
int N, cnt;

void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
}

int main()
{
	fast_io();
	cin >> N;
	while (N--)
	{
		int y, x; cin >> y >> x;
		for (int i = y; i < y + 10; i++)
		{
			for (int j = x; j < x + 10; j++)
			{
				if (paper[i][j] == 0)
				{
					paper[i][j] = 1;
					cnt++;
				}
			}
		}
	}
	cout << cnt;
}

  전체 영역중 입력한 좌표에서 +10 범위 안의 영역을 1로 칠하면 겹치는 부분이 생길 때 0이 아니면 그대로 유지되기 때문에 중복 영역을 복잡하게 생각할 필요가 없는 문제였다.

시간복잡도 : O(N^2)