- 문제
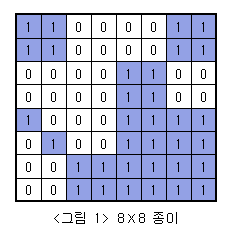
아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.![]
전체 종이의 크기가 N×N(N=2k, k는 1 이상 7 이하의 자연수) 이라면 종이를 자르는 규칙은 다음과 같다.
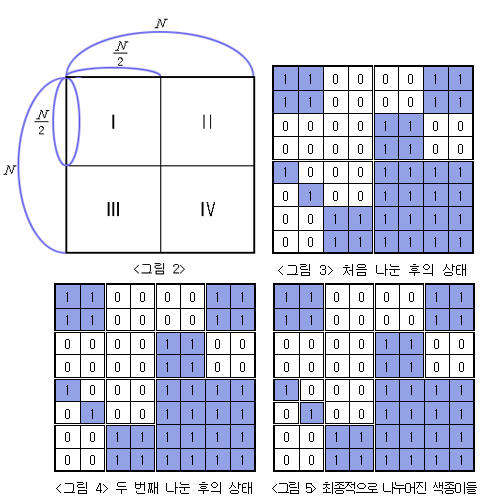
전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 N/2 × N/2색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.
위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.
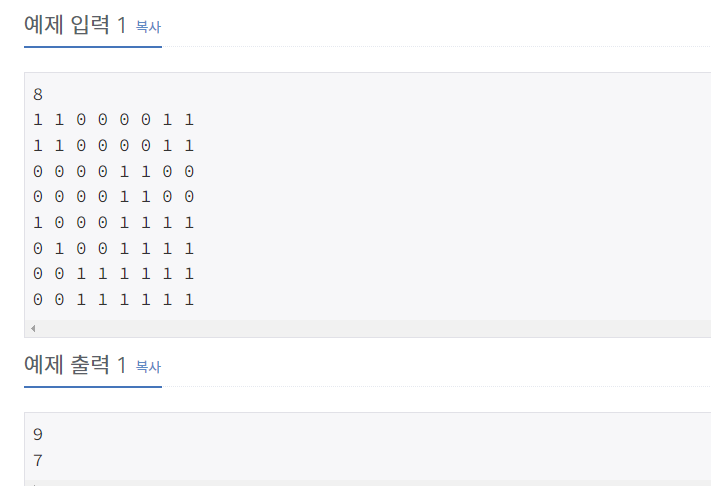
입력으로 주어진 종이의 한 변의 길이 N과 각 정사각형칸의 색(하얀색 또는 파란색)이 주어질 때 잘라진 하얀색 색종이와 파란색 색종이의 개수를 구하는 프로그램을 작성하시오.- 입력
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 하얀색으로 칠해진 칸은 0, 파란색으로 칠해진 칸은 1로 주어지며, 각 숫자 사이에는 빈칸이 하나씩 있다.- 출력
첫째 줄에는 잘라진 햐얀색 색종이의 개수를 출력하고, 둘째 줄에는 파란색 색종이의 개수를 출력한다.
#include<iostream>
using namespace std;
int arr[129][129];
int N; int White_count = 0, Blue_count = 0;
void fast_io()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
}
void cut_off(int x, int y, int num)
{
bool Zero = true, One = true;
for (int i = x; i < x + num; i++)
{
for (int j = y; j < y + num; j++)
{
if (arr[i][j] == 1)
{
Zero = false;
}
if (arr[i][j] == 0)
{
One = false;
}
}
}
if (Zero)
{
White_count++;
return;
}
if (One)
{
Blue_count++;
return;
}
cut_off(x, y, num / 2);
cut_off(x, y + num / 2, num / 2);
cut_off(x + num / 2, y, num / 2);
cut_off(x + num / 2, y + num / 2, num / 2);
}
int main()
{
cin >> N;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> arr[i][j];
}
}
cut_off(0, 0, N);
cout << White_count << '\n' << Blue_count;
} 재귀 & Divide&Conquer 문제로 각 영역이 0 또는 1로만 가득 차있는지 확인 후 영역 분할을 위해 재귀함수를 수행할 좌표를 적절하게 넣어주면 되는 문제이다 (각 사분면의 시작 위치를 현위치+변의길이/2로 두면 된다)
재귀 함수의 세번째 인자에서 변의 길이를 축소시키기 때문에 최종적으로 길이가 1짜리인 사각형까지 체크하게 된다.
시간복잡도 : O(n^2)?
0인지 1인지 확인하는 과정에서 중첩 반복문이 돌아가기 때문에 n^2의 시간으로 추정