점화식(재귀식)

점화식 (재귀식)

점화식(재귀식)이란 수열에서 이웃하는 두 개의 항 사이에 성립하는 관계를 나타낸 관계식이다.

대표적인 점화식

• 등차 수열: F(n) = F(n-1) + a *a: 고정된 상수
• 등비 수열: F(n) = F(n-1) * a
• 팩토리얼: F(n) = F(n-1) * n
• 피보나치 수열: F(n) = F(n-1) + F(n-2)

ex) 등차수열

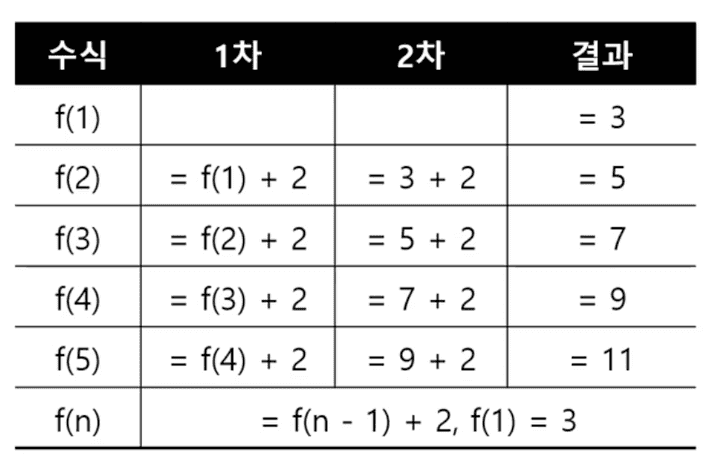
등차수열

F(n) = F(n-1) + a

for문

다음 예제의 파라미터에서 각각 의미하는 값은 s는 f(1)일 때 시작하는 값, t는 간격, number는 등차수열의 몇번째 값을 구할것인지 f(n)의 n을 의미한다.

let result;

function forloop(s, t, number) {
  let acc = 0;

  for (let i = 1; i <= number; i++) {
    if ((i = 1)) acc += s;
    else acc += t;

    console.log(i, acc);
  }

  return acc;
}
result = forloop(3, 2, 5);
console.log(result);

# output
1 3
2 5
3 7
4 9
5 11
11

재귀함수

let result;

function recursive(s, t, number) {
  // 멈출 조건
  if (number == 1) {
    return s;
  }

  // 반복할 코드
  return recursive(s, t, number - 1) + t;
}

result = recursive(3, 2, 5);
console.log(result);

재귀 과정

s = 3, t = 2, number = 5 → recursive(3, 2, 4) + 2;
s = 3, t = 2, number = 4 → recursive(3, 2, 3) + 2;
s = 3, t = 2, number = 3 → recursive(3, 2, 2) + 2;
s = 3, t = 2, number = 2 → recursive(3, 2, 1) + 2;
s = 3, t = 2, number = 1 → number = 1 중단 조건 → return s;  = 3
// 여기서 종료되었으므로 다시 거꾸로 올라가면서 계산한다.
s = 3, t = 2, number = 2 → 3 + 2 = 5
s = 3, t = 2, number = 3 → 5 + 2 = 7
s = 3, t = 2, number = 4 → 7 + 2 = 9
s = 3, t = 2, number = 5 → 9 + 2 = 11

등비수열

F(n) = F(n-1) * a

for문

let result;

function forloop(s, t, number) {
  let acc = 1;

  for (let i = 1; i <= number; i++) {
    if ((i = 1)) acc *= s;
    else acc *= t;

    console.log(i, acc);
  }

  return acc;
}

result = forloop(3, 2, 5);
console.log(result);

# output
1 3
2 6
3 12
4 24
5 48
48

재귀함수

let result;

function recursive(s, t, number) {
  // 멈출 조건
  if (number == 1) {
    return s;
  }

  // 반복할 코드
  return recursive(s, t, number - 1) * t;
}

result = recursive(3, 2, 5);
console.log(result);

팩토리얼

F(n) = F(n-1) * n

let result;

function recursive(number) {
  if (number == 1) return number;

  return recursive(number - 1) * number;
}

result = recursive(5);
console.log(result);

피보나치 수열

F(n) = F(n-1) + F(n-2)

let result;

function recursive(number) {
  if (number == 1 || number == 0) return number;

  return recursive(number - 1) + recursive(number + 2);
}
result = recursive(5);
console.log(result);