경우의 수 (순열과 조합)

경우의 수

어떤 사건 혹은 일이 일어날 수 있는 경우의 가짓수를 수로 표현한 것이다.

그 중 완전 탐색으로 경우의 수를 푸는 대표적 알고리즘으로는 순열과 조합이 있다.

재귀함수 이해하기

들어가기 앞서, 순열과 조합을 구할 때 사용되는 재귀함수에 대해서 먼저 이해하고 넘어가자.

재귀함수는 내부적으로 자기 자신을 호출하는 함수이다. 반드시 종료 조건이 필요하다는 특징을 가지고 있다.

재귀 호출을 너무 많이 하게되면 스택 메모리 영역에 너무 많은 공간을 할당하게 되어 스택 오버플로가 발생할 수 있다는 점을 주의해야 한다. 그래서 재귀 함수를 구현할 때는 최악의 경우 얼마나 많은 재귀 호출이 발생하는지 잘 살펴보아야 한다.

function counter(count) {
  // 재귀 호출 종료 조건
  if (count == 5) {
    return;
  }
  console.log(1);
  counter(count + 1); // 재귀 호출
  console.log(2);
}

counter(0);

# output
1
1
1
1
1
2
2
2
2
2

👌 종료 조건을 만족할 때 일어나는 일

재귀호출 후 종료 조건에 도달했을 때 실행 과정을 하나하나 풀어서 써보았다.

• counter(0) 시작
• 재귀 호출을 반복하다가 counter(5)가 호출되면 count 값이 5가 되어 종료 조건 만족
• return 문을 만나 counter(5) 종료
• counter(4)에서 counter(5)를 호출했던 위치의 다음 로직으로 2를 출력
• counter(4) 종료
• counter(3)에서 counter(4)를 호출했던 위치의 다음 로직으로 2를 출력
• counter(3) 종료
• counter(2)에서 counter(3)을 호출했던 위치의 다음 로직으로 2를 출력
• counter(2) 종료
• counter(1)에서 counter(2)을 호출했던 위치의 다음 로직으로 2를 출력
• counter(1) 종료
• counter(0) 에서 counter(1)을 호출했던 위치의 다음 로직으로 2를 출력
• counter(0) 함수 종료

이 과정을 그림으로 보면 다음과 같다.

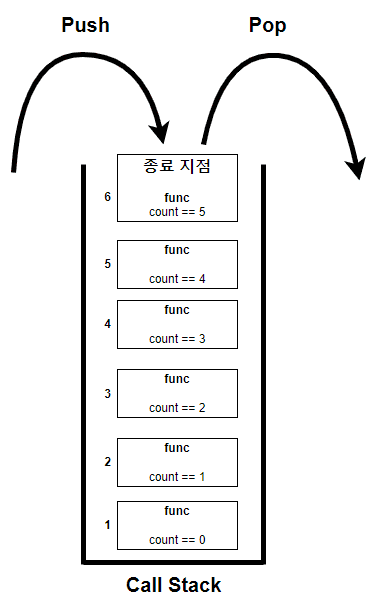
함수가 호출될 때 공간이 할당되고 종료하면서 해제되는 메모리 영역을 Call Stack으로 나타낸다.

함수가 호출되면 스택 프레임(네모 상자)이 push(메모리 할당)되고, 함수가 종료되면 스택 프레임이 pop(메모리 할당 해제) 된다.

func라고 적혀있는 상자가 함수와 관련하여 할당된 메모리(스택 프레임)라고 할 수 있다.

옆에 적힌 숫자 1 ~ 6 순서로 push되고, 6 ~ 1 순서로 pop된다.

6번 스택 프레임이 count == 5 연산 결과가 true가 되어 재귀 호출을 종료하게 되는 지점이다. 종료 지점을 만나기 전에는 스택 프레임을 계속해서 push하고 종료 조건을 만족시킬때 pop한다.

재귀 호출이 종료되고 나면 재귀 호출 바로 다음 로직을 실행하는 흐름을 타게 된다.

순열

서로 다른 n개의 원소 중에서 r를 중복 없이 골라 순서에 상관있게 나열하는 경우의 수 (nPr)

nPr = n! / (n-r)!

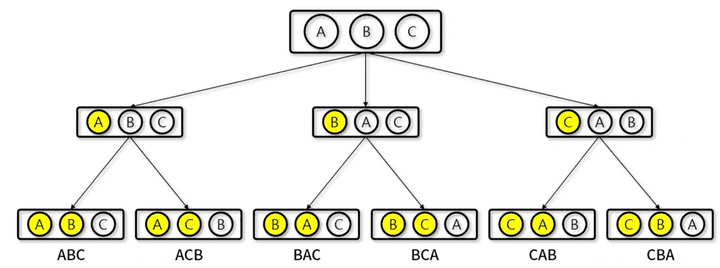
ex) 3개의 알파벳으로 단어를 만드는 경우의 수

for문

3개의 알파벳으로 단어를 만들어야 하므로, 알파벳을 중복없이 순서와 상관있게 3번 선택하게 될 것이다. 3번의 선택에 따른 3개의 변수를 지정해주게 되기 때문에 for문이 3개 들어가게 된다.

• i = 0 으로 시작해서 첫번째 선택한 알파벳은 ‘a’
• 다음 반복문에서 j = 0으로 똑같이 배열의 0번째인 알파벳 a를 고르게 되므로 if (i == j) continue 조건을 만나서 스킵되고 j = 1 일 때에 반복문으로 넘어간다. 그러면 두번째로 선택한 알파벳은 ‘b’가 된다.
• 마지막으로 k = 0에서 시작하여 마찬가지로 첫번째 두번째 선택한 알파벳과 겹치지 않도록 i, j 와 k 가 같을 경우 스킵하도록 작성해서 세 개의 중복되지 않는 선택하는 경우의 수를 출력할 수 있다.

// for문을 통한 순열
let input = ['a', 'b', 'c'];
let count = 0;

function permutation(arr) {
  // for i : 첫번째 index에 위치시킬 요소 [i, , ]
  for (let i = 0; i < arr.length; i++) {
    // for j : 두번째 index에 위치시킬 요소 [i, j, ]
    for (let j = 0; j < arr.length; j++) {
      // i 와 중복되면 안되니까 i == j 라면 스킵
      if (i == j) continue;
      // for k : 세번째 index에 위치시킬 요소 [i, j, k]
      for (let k = 0; k < arr.length; k++) {
        if (i == k) continue;
        if (j == k) continue;

        console.log(arr[i], arr[j], arr[k]);
        count++;
      }
    }
  }
}

permutation(input);
console.log(count);

// ouput
a b c
a c b
b a c
b c a
c b a
c a b
6

❓ break / continue 차이

• break: 반복문 내에서 지정한 조건을 만나면 더 이상 반복하지 않고 반복문을 끝낸다.
• continue: 반복문 내에서 지정한 조건을 만나면 continue 아래에 있는 실행해야 하는 문장을 건너 뛰고, 다음 반복을 시작한다.

선택하는 개수만큼 for문의 개수가 늘어나고 있다. 요소가 너무 많아지면 for문으로 대처하는데에 한계가 있기 때문에 그럴때 재귀함수를 주로 사용한다.

재귀함수

아래의 예제는 재귀함수를 사용해 매개변수만 수정하면서 스스로를 다시 호출, 로직을 돌며 배열 아이템의 순서가 동일한 경우는 위치를 그대로 두고, 다를 경우에는 앞뒤의 위치를 바꿔주는 방식으로 경우의 수를 도출한 방법이다.
매개변수에는 (배열, 시작위치(=배열의 시작할 인덱스), 선택할 요소 개수(=배열의 마지막 인덱스))를 준다.

// 재귀를 통한 순열
let input = ['a', 'b', 'c'];
let count = 0;

function permutation(arr, s, r) {
  // 1. 재귀함수를 멈춰야 할 조건
  if (s == r) {
    count++;
    console.log(arr.join(' '));
    return;
  }

  // 2. 재귀를 돌면서 변경되어야 할 부분
  for (let i = s; i < arr.length; i++) {
    [arr[s], arr[i]] = [arr[i], arr[s]]; // swap
    permutation(arr, s + 1, r);
    [arr[s], arr[i]] = [arr[i], arr[s]]; // 원상복귀
  }
}

permutation(input, 0, 2);
console.log(count);

재귀함수를 사용할 때는 시작할 위치를 정하고, swap을 통해서 경우의 값을 도출한다.

i = 0이 아닌 i = s인 이유는 0으로 시작할 경우 배열에서 중복해서 계속 뽑을 수 있기 때문에 변수로 주어, 선택된 값은 뽑지 않도록 설정해준다.

그 다음 permutation(arr, s+1, r) 자기 자신 함수를 호출하는데 처음 선택과 중복된 값을 뽑지 않도록 시작하는 위치 매개변수에 s+1 값을 넘겨준다.

과정

// permutation(arr, 0, 2)
s = 0, i = 0, r = 2 → [0,0] = [0,0] → [a,b,c] → 재귀호출

// permutation(arr, 1, 2)
s = 1, i = 1, r = 2 → [1,1] = [1,1] → [a,b,c] → 재귀호출

// permutation(arr, 2, 2)
s = 2, i = 2, r = 2 →  (s == r) 재귀함수 종료: count++하고 그전까지의 arr를 출력한다.
swap이 없었으므로 [a, b, c] 출력 return;

// 재귀함수가 종료된 조건 이전의 재귀함수로 돌아간다. 재귀함수 호출코드 아래 코드 실행
// permutation(arr, 1, 2)
s = 1, i = 1, r = 2 → [1,1] = [1,1] : [a,b,c]

i++
s = 1, i = 2, r = 2 → [1,2] = [2,1] → [b,c] = [c,b] : swap [a,c,b] → 재귀호출

// permutation(arr, 2, 2)
s = 2, i = 2, r = 2 → (s == r) 재귀함수 종료: count++ [a,c,b] 출력 return;

// 재귀함수가 종료된 조건 이전의 재귀함수로 돌아간다. 재귀함수 호출코드 아래 코드 실행
// permutation(arr, 1, 2)
s = 1, i = 2, r = 2 → [1,2] = [2,1] → [c,b] = [b,c] : swap [a,b,c]
i = 2로 반복문 종료

// 재귀함수가 종료된 조건 이전의 재귀함수로 돌아간다. 재귀함수 호출코드 아래 코드 실행
// permutation(arr, 0, 2)
s = 0, i = 0 → [0,0] = [0,0] → [a,a] = [a,a] → [a,b,c]

i++
s = 0, i = 1 → [0,1] = [1,0] → [a,b] = [b,a] → [b,a,c]
.
.
.
s = 0, i = 2 → [0,2] = [2,0] → [a,c] = [c,a] → [c,a,b]

❓ swap
Array에서 두 요소를 서로 바꾸고 싶은 경우, swap을 해야하는데 JavaScript에는 별도의 swap 메서드가 없기 때문에 직접 사용해야 한다.

그 중 구조 분해 할당을 사용하여 배열을 해체한 뒤, 그 값을 개별 변수에 담을 수 있다.

const arr = [1, 2, 3, 4, 5];
[arr[1], arr[2]] = [arr[2], arr[1]];
console.log(arr); // [1,3,2,4,5]

단순히 2개의 대상만을 서로 swap 하는 것이 아니라 사용자가 정의하는대로 n개의 요소의 위치를 변경할 수 있다.

const arr = [1, 2, 3, 4, 5];
[arr[1], arr[2], arr[4]] = [arr[2], arr[4], arr[1]];
console.log(arr); // [1,3,5,4,2]

조합

서로 다른 n개의 원소 중에서 r를 중복 없이 골라 순서에 상관없이 나열하는 경우의 수 (nCr)

nCr = n! / (n-r)! r!

ex) 4개의 숫자 카드에서 2개를 뽑는 경우의 수

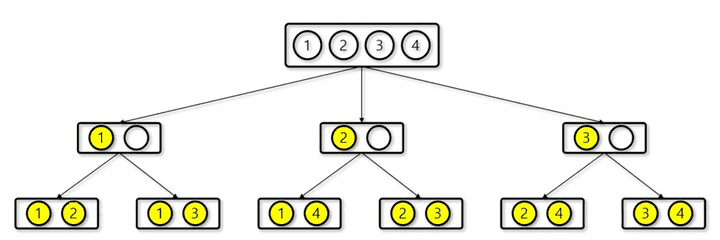
for문

let input = [1, 2, 3, 4]; // 4C2
let count = 0;

function combination(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = i + 1; j < arr.length; j++) {
      count++;
      console.log(arr[i], arr[i]);
    }
  }
}

combination(input);
console.log(count);

# output
1 2
1 3
1 4
2 3
2 4
3 4

재귀함수

매개변수로 (배열, 아웃풋이 저장될 데이터, 시작하는 위치, 현재 위치 정보, 선택할 요소 개수)를 주었다.

let input = [1, 2, 3, 4];
let output = [];
let count = 0;

function combination(arr, data, s, idx, r) {
  if (s == r) {
    count++;
    console.log(data);
    return;
  }
  for (let i = idx; arr.length - i >= r - s; i++) {
    data[s] = arr[i];
    combination(arr, data, s + 1, i + 1, r);
  }
}

combination(input, output, 0, 0, 2);
console.log(count);

과정

// combination(input, output, 0, 0, 2)
s = 0, idx(i) = 0, r = 2 → data[0] = 1; → 재귀호출

// combination(input, output, 1, 1, 2)
s = 1, idx(i) = 1, r = 2 → data[1] = 2; → 재귀호출

// combination(input, output, 2, 2, 2)
s = 2, idx(i) = 2, r = 2 → s == r 재귀함수 종료 → count++ [1,2] 출력 return;

// 재귀함수가 종료된 조건 이전의 재귀함수로 돌아간다. 재귀함수 호출코드 아래 코드 실행 (없으므로 i++)
// combination(input, output, 1, 1, 2)
i++
s = 1, idx(i) = 2, r = 2 → data[1] = 3; → 재귀호출

// combination(input, output, 2, 3, 2)
s = 2, idx(i) = 3, r = 2 → s == r 재귀함수 종료 → count++ [1,3] 출력 return;

// 재귀함수가 종료된 조건 이전의 재귀함수로 돌아간다. 재귀함수 호출코드 아래 코드 실행 (없으므로 i++)
// combination(input, output, 1, 2, 2)
i++
s = 1, idx(i) = 3(*for문 종료), r = 2 → data[1] = 4; → 재귀호출

// combination(input, output, 2, 4, 2)
s = 2, idx(i) = 4, r = 2 → s == r 재귀함수 종료 → count++ [1,4] 출력 return;
반복문 종료

// 재귀함수가 종료된 조건 이전의 재귀함수로 돌아간다. 재귀함수 호출코드 아래 코드 실행 (없으므로 i++)
// combination(input, output, 0, 0, 2)
i++
s = 0, idx(i) = 1, r = 2 → data[0] = 2; → 재귀호출

// combination(input, output, 1, 2, 2)
s = 1, idx(i) = 2, r = 2 → data[1] = 3; → 재귀호출

// combination(input, output, 2, 3, 2)
s = 2, idx(i) = 3, r = 2 → s == r 재귀함수 종료 → count++ [2,3] 출력 return;

// 재귀함수가 종료된 조건 이전의 재귀함수로 돌아간다. 재귀함수 호출코드 아래 코드 실행 (없으므로 i++)
// combination(input, output, 1, 2, 2)
i++
s = 1, idx(i) = 3(*for문 종료), r = 2 → data[1] = 4; → 재귀호출

// combination(input, output, 2, 4, 2)
s = 2, idx(i) = 4, r = 2 → s == r 재귀함수 종료 → count++ [2,4] 출력 return;

// combination(input, output, 0, 1, 2)
i++
s = 0, idx(i) = 2, r = 2 → data[0] = 3; → 재귀호출

// combination(input, output, 1, 3, 2)
s = 1, idx(i) = 3, r = 2 → data[1] = 4; → 재귀호출

// combination(input, output, 2, 4, 2)
s = 2, idx(i) = 4, r = 2 → s == r 재귀함수 종료 → count++ [3,4] 출력 return;

출처

• 경우의 수를 찾는 방법 - 순열, 조합 그리고 재귀함수
• [Node.js] javascript: Array의 요소(element)를 swap하는 방법
• MDN 구조 분해 할당
• 재귀함수 예제로 이해하기, 3가지 규칙