Part 1. Mathematical Foundations 수학적 기초 (작성중)

2. Linear Algebra 선형대수학

when formalizing intuitive concepts, a common approach is to construct a set of objects (symbols) and a set of rules to manipulate these objects.
직관적인 개념을 공식화할 때 일반적인 접근 방식은 일련의 개체(기호)와 이러한 개체를 조작하는 규칙 집합을 구성하는 것이다.

This is known as an algebra.
이것은 대수학으로 알려져 있다.

Linear algebra is the study of vectors and certain rules to manipulate vectors.
선형대수학은 벡터와 벡터를 다루는 규칙에 대한 공부이다.

The vectors many of us know from school are called “geometric vectors”, which are usually denoted by a small arrow above the letter, e.g., $\vec{x}$ and $\vec{y}$.
우리 중 많은 사람들이 학교에서 알고 있는 벡터를 "기하학적 벡터"라고 하며 일반적으로 문자 위의 작은 화살표로 표시된다.

In this book, we discuss more general concepts of vectors and use a bold letter to represent them, e.g., $x$ and $y$.
이 책에서는 보다 일반적인 벡터의 개념에대해 논의하고 볼드체를 사용하여 이를 나타낸다.

In general, vectors are special objects that can be added together and multiplied by scalars to produce another object of the same kind.
일반적으로 벡터는 같은 종류의 다른 객체를 생성하기 위해 함께 더하고 스칼라로 곱할 수 있는 특수 객체이다.

From an abstract mathematical viewpoint, any object that satisfies these two properties can be considered a vector. Here are some examples of such vector objects:
추상적인 수학적 관점에서 이 두 가지 속성을 만족하는 모든 객체는 벡터로 간주될 수 있다.
다음은 그러한 몇가지 예시이다.

1. Geometric vectors. This example of a vector may be familiar from high school mathematics and physics.
1. 기하학적 벡터. 벡터의 이 예는 고등학교 수학 및 물리학에서 친숙하다.

Geometric vectors (see Figure 2.1(a)) are directed segments, which can be drawn (at least in two dimensions).
기하학적 벡터 (그림2.1(a)참조)는 (적어도 2차원으로) 그릴 수 있는 방향 세그먼트이다.

Two geometric vectors $\vec{x}+\vec{y}$ can be added, such that $\vec{x}+\vec{y} = \vec{z}$ is another geometric vector.
두 기하벡터 $\vec{x}+\vec{y}$ 는 더해질 수 있으므로 $\vec{x}+\vec{y} = \vec{z}$ 는 또 다른 기하 벡터이다.

Furthermore, multiplication by a scalar $\lambda \vec{x}, \lambda \in R$, is also a geometric vector.
또한 스칼라 $\lambda \vec{x}$($\lambda \in R$)의 곱도 기하 벡터이다.

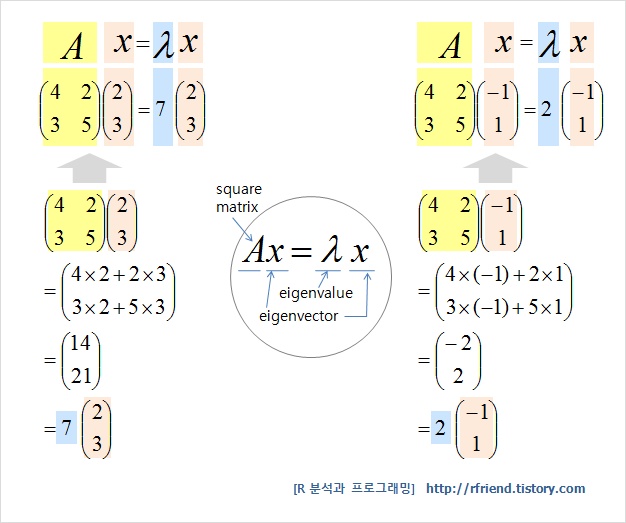
• $\lambda$ = 람다 (선형대수에서는 *고유값을 나타낸다)
• $R$ = 실수

*정방행렬 A에 대하여 Ax = λx  (상수 λ) 가 성립하는 0이 아닌 벡터 x가 존재할 때
상수 λ 를 행렬 A의 고유값 (eigenvalue), x 를 이에 대응하는 고유벡터(eigenvector) 라고 함

• 정방행렬(square matrix) = 열과 행의 길이가 같은 행렬
  Reference

In fact, it its the original vector concepts introduced previously.

사실 그건 이전에 소개된 원래의 벡터 개념이다.

Therefore, geometric vectors are instances of the vector concepts introduced previously.

따라서 기하학적 벡터는 이전에 도입된 벡터 개념의 인스턴스(경우,사례)이다.

Interpreting vectors as geometric vectors enables us to use our intuitions about direction and magnitude to reason about mathematical operations.

벡터를 기하학적 벡터로 해석하면 방향과 크기에 대한 직관을 사용하여 수학적 연산에 대해 추론할 수 있습니다.

2. Polynomials are also vectors; see Figure 2.1(b): Two polynomials can