1. 소수의 판별

풀이

• 소수는 약수가 1과 자신 총 2개인 수 의미한다.
• 따라서 isPrime함수에 전달된 int형 정수가 1이면, 약수가 1개이므로 소수X
• 1이 아니면, 2~(자기자신-1)까지 반복해 % 연산을 해주며, 하나라도 나머지가 0인 경우가 발생한다면 소수가 X므로 break 후 false를 출력한다.
• 이때 시간복잡도를 O(N) -> O(루트N) 으로 줄일 수 있다.
  만약 data=12면, 약수는 1,2,3,4,6,12이다.
  가운데를 기준으로 왼쪽 a, 오른쪽 b면 a<=b이다.
  여기서 a==b인 경우를 보면 a=b=루트12인 상황이다.
  즉, 반복문을 (data-1)까지 비교하지 않고 a를 (2~루트data)까지 한다면,
  시간복잡도를 루트n으로 크게 줄일 수 있을 것이다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>//동적 배열
#include <algorithm>
#include <ctime>
using namespace std;

//자연수 T가 소수인지 판별해 Y/N 출력
//소수는 약수가 1과 자신 총 2개인 수 의미

//소수 판별 함수
bool isPrime(int data) {

      //만약 data가 1이면, 약수 자기자신 1개로 소수X
    if (data == 1) return false;

    //2부터 (자신-1)까지 반복하며 나머지 0인 수가 있다면, 소수X
    /*
    but, 시간복잡도 루트n으로 가능
    data=12면 약수는 1,2,3,4,6,12이다.
    가운데를 기준으로 왼쪽 a, 오른쪽 b면 a<=b이다.
    여기서 a==b인 경우는 a=b=루트12인 상황이다.
    즉, data까지 비교하지 않고 a를 (2~루트data)까지 한다면,
    시간복잡도는 루트n으로 크게 줄일 수 있을 것이다.
    */
    
    int cnt = 1;//1은 기본으로 포함한 상태
    for(int i = 2; i*i<=data; i++){
        
        //2~루트data 중 하나라도 나눠지면 소수X
        if (data % i == 0) return false;
    }
    
    //앞의 모든 조건문에 걸리지 않으면 true
    return true;
}


int main() {
    
    int T;
    int* data;
    bool* result;

    //테스트 케이스 수 입력
    cin >> T;
    data = new int[T];

    //T개의 자연수 입력(10억 이하 => int)
    for (int i = 0; i < T; i++) {
        cin >> data[i];
    }
    
    result = new bool[T];
    //소수판별 함수 호출
    for (int i = 0; i < T; i++) {
        result[i] = isPrime(data[i]);
    }

    
    //결과 출력
    for (int i = 0; i < T; i++) {
        cout << "Case #" << i + 1 << endl;
        if (result[i] == false) {
            cout << "NO" << endl;
        }
        else {
            cout << "YES" << endl;
        }
    }
   
    return 0;
}

문제2. 데스트니

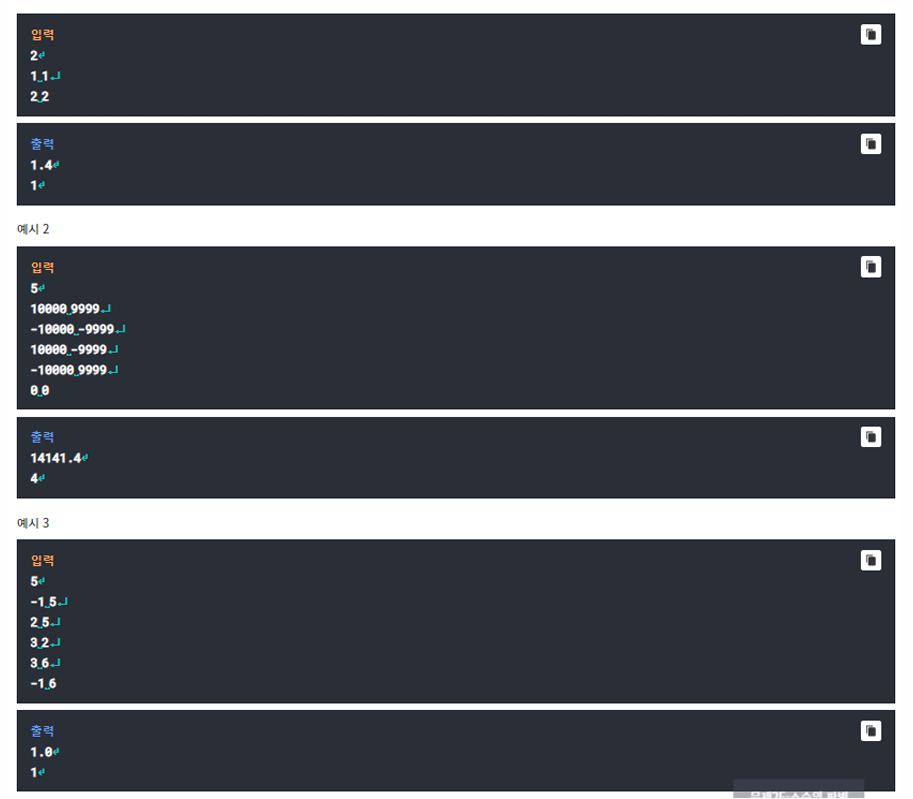
풀이

• 두 좌표를 입력받기 때문에 x,y를 멤버 변수로 가지는 Point2D 클래스를 생성했다.
• 두 좌표 사이의 거리를 구하는 공식은 {루트(x2-x1)^2 + (y2-y1)^2}이므로, 루트 내부를 계산하는 멤버 함수 getSqd(), 루트를 씌운 거리값을 계산하는 getDistance() 멤버 함수를 작성해 줬다.
• 이렇게 두 단계로 나누어 함수를 작성한 이유는 main() 에서 현재 두 좌표간의 거리와 현재까지 최소 두 좌표간의 거리를 비교할 때, int 형으로 비교하기 위해서다.
• 정확히 말하면, 두 함수를 하나로 만들어 거리 double 값을 리턴해 비교하게 되면, 부동소수점의 비교연산에는 오차가 발생해 부정확한 비교 결과가 나올 수 있다.
• 따라서 일부러 한번에 거리를 계산하지 않고, 거리의 제곱을 int로 반환해서 비교해 정확한 비교가 가능하도록 한 것이다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>//동적 배열
#include <algorithm>
#include <cmath>
using namespace std;

//중복X N개의 좌표쌍 입력받아 
//가장 가까운 두 천제 사이 거리 소수점 두번째자리 반올림 출력
//그 거리만큼 떨어진 전체 쌍의수 출력

class Point2D {
private:
    int x;
    int y;
public:
    //생성자
    Point2D(int x = 0, int y = 0) {
        this->x = x;
        this->y = y;
    }

    //두 좌표 사이 거리의 제곱 계산 함수
    int getSqd(const Point2D target)const {
        int dx = abs(this->x - target.x);//x좌표사이 거리
        int dy = abs(this->y - target.y);//y좌표사이 거리
        return dx * dx + dy * dy;
    }

    //두 천체 사이 거리 반환 함수 {루트(x2-x1)^2 + (y2-y1)^2}
    double getDistance(Point2D data) {
        double sqd = (double) this->getSqd(data);//두 좌표사이 거리 제곱 반환해
        return sqrt(sqd);//루트씌운값 리턴
    }
};

int main() {

    int n;
    Point2D* data;

    cin >> n;
    data = new Point2D[n];

    //n개의 x,y 좌표 입력
    for (int i = 0; i < n; i++) {
        int x, y;
        cin >> x >> y;
        //생성자 호출
        data[i] = Point2D(x, y);
    }

    int min_sqd = INT_MAX;//int값의 최댓값 21억 초기값
    int min_cnt = 0;
    
    //버블 정렬처럼 i에 대해 j를 증가시키며, 0~(i-1)까지 거리 계산
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < i; j++) {

            //i와 두 좌표사이 거리 제곱 계산(int로 비교)
            int sqd = data[i].getSqd(data[j]);

            //최소 sqd를 갱신
            if (min_sqd > sqd) {
                min_sqd = sqd;
                min_cnt = 1;//갱신된 최소sqd로 다시 카운팅
            }
            //거리가 현재 최소sqd와 같은 경우 개수 카운팅
            else if(min_sqd == sqd) {
                min_cnt++;
            }
        }
    }
   

    //결과 출력
    double min_dis = sqrt(min_sqd);//최소거리 제곱을 루트씌워 출력
    printf("%.1f\n", min_dis);
    printf("%d\n", min_cnt);

    return 0;
}

문제3. 버블정렬

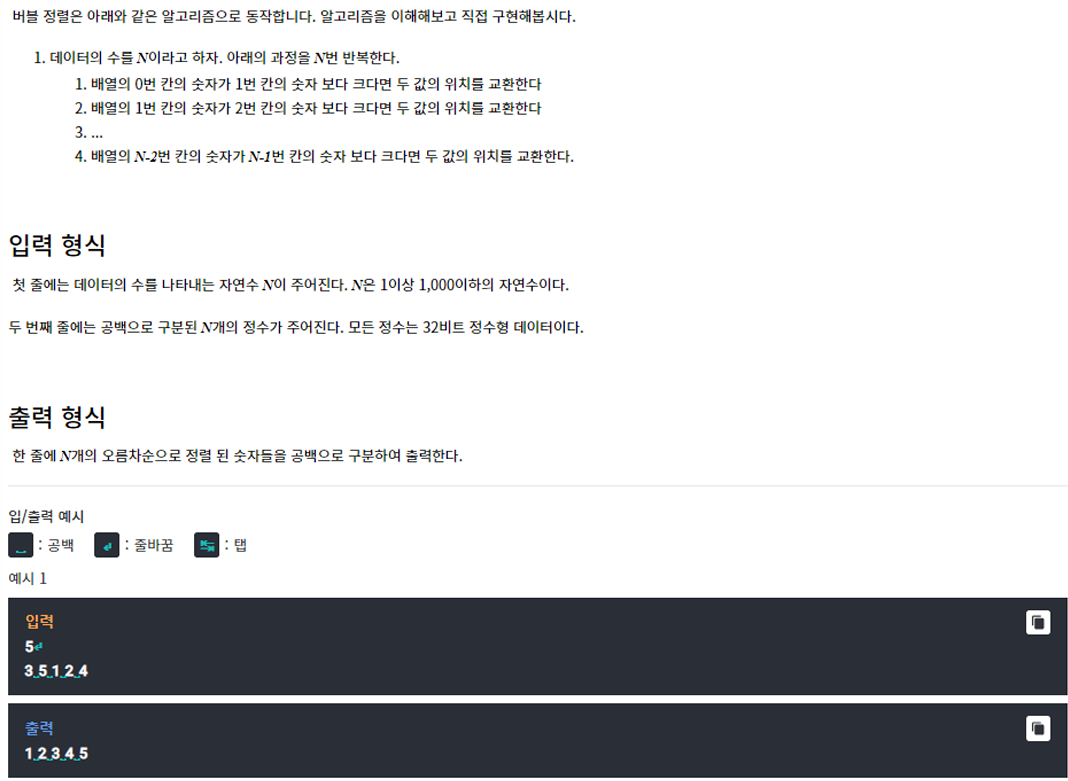
풀이

• 버블정렬로 오름차순 정렬을 해보자. 먼저 i=0부터 1회 루프시마다 (n-1)-i에 가장 큰 원소가 정렬되게 된다.
• 따라서 내부 for문은 j < (n-i)까지 루프를 돌게하여, 이미 정렬된 (n-i)번째 원소는 비교에 포함하지 않게 해준다.
• j=1로 설정한 것은 조건문에서 j-1과 j를 비교할 것이므로 이렇게 설정했다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>//동적 배열
#include <algorithm>
#include <cmath>
using namespace std;

//버블정렬해 오름차순 정렬
void bubbleSort(int arr[], int n) {
    
    //i에 대해 j를 i+1~n까지 증가시키며 정렬
    for (int i = 0; i < n; i++) {
        
        int cnt = 0;//정렬 여부 확인 카운터
        for (int j = 1; j < n-i; j++) {

            //이전 원소가 더 크면 swap
            if (arr[j-1] > arr[j]) {
                int temp = arr[j];
                arr[j] = arr[j -1];
                arr[j - 1] = temp;
                cnt++;//원소 교환시마다++
            }
        }
        if (cnt == 0) break;//이미 정렬되어있으면 연산중단
    }
}

int main() {

    int n;
    int* data;

    cin >> n;
    data = new int[n];

    //비정렬된 n개의 정수 입력
    for (int i = 0; i < n; i++) {
        cin >> data[i];
    }
    
    bubbleSort(data, n);

    //결과 출력
    for (int i = 0; i < n; i++) {
        cout << data[i] << " ";
    }

    delete[] data;
    return 0;
}

문제4. 픽셀 수 세기

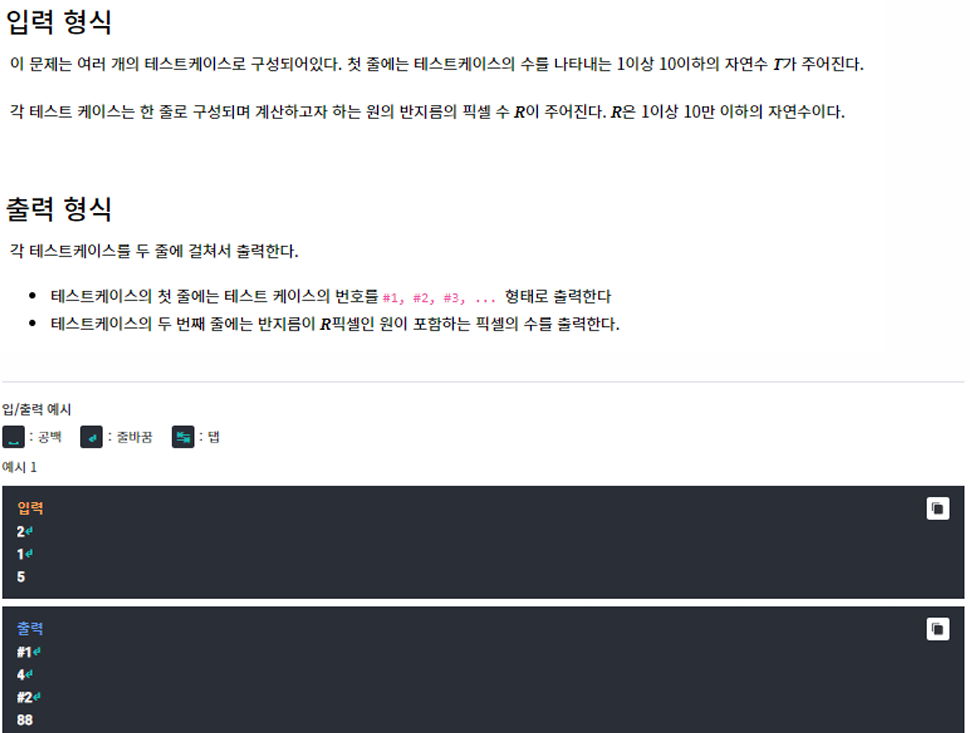
• 먼저 원은 대칭이므로 4등분해서 1사분면만 생각해 픽셀 수를 카운트 한 다음 * 4를 해주면 전체 픽셀 수를 셀 수 있다.
• 1사분면이므로 원의 중심은 (0,0)에 위치하고 x,y 좌표값은 증가할 것이다.
• 먼저 2중 for문을 통해 외부 for문에서 x는 0부터 증가시키고, 내부 for문에서 y는 최댓값인 R부터 0까지 줄어들며 최초로 포함되는 y를 찾아낼 것이다
• 즉 x좌표에 대해 그룹을 나누고, 그때마다의 y값의 최대치를 height에 더해 픽셀 수를 기록하는 것이다.
  
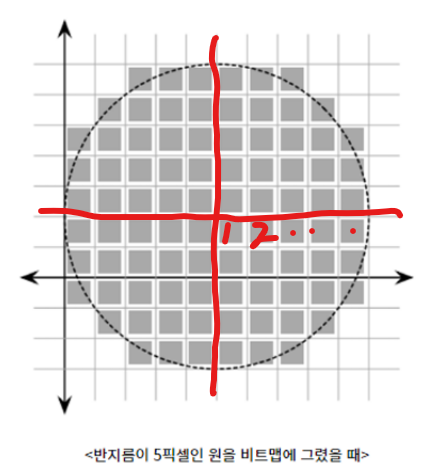
• isInside() 함수로 매 (x,y)쌍마다 R과 함께 인자로 전달해 원 범위 안에 들어오는지를 확인해 봐야 한다.
• 해당 함수에서는 원의 방정식(x^2 + y^2 = R^2)을 이용해서 인자 x,y가 R범위 안에 들어오는지를 확인한 후 bool 값을 리턴해준다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

//T개의 반지름 R을 입력받고 해당 원에 들어갈수 있는 픽셀 수 출력
//R=5인 원은 직경에 10픽셀이 포함된다.

//좌표 (x,y)가 주어진 원 안에 포함되는지 여부 반환 함수
bool isInside(long long x, long long y, long long R) {
    
    //x^2 + y^2 < R^2 
    long long sqd = x * x + y * y;
    if (sqd < R * R) {
        return true;
    }
    return false;
}

void testcase(int idx) {
    
    long long R;//출력 결과 값이 int범위 넘어서므로
    cin >> R;

    //원은 대칭이므로 4등분해 1사분면*4로 계산해도 총 픽셀 수 계산 가능
    
    long long sum = 0;//1사분면에 존재하는 총 픽셀 수
    long long y = R;

    //1사분면이므로 원 중심은 (0,0)부터 증가 
    //따라서 x를 0부터 증가시키고
    for (long x = 0; x <= R; x++) {
        long long height = 0;

        //x에 대한 y를 최대높이인 R부터 0까지 감소시키며
        for (; y >= 0; y--) {
            if (isInside(x, y, R)) {
                //최초로 원 안에 포함된 픽셀 좌표의
                //y+1이 한x에 대한 그룹의 높이가 된다.
                height = (y + 1);
                break;
            }
        }
        sum += height;
    }
    printf("#%d\n", idx);
    printf("%lld\n", sum * 4);//*4 해줘서 전체 사분면 픽셀 수 센다.

}

int main() {

    int t;
    
    //테스트 케이스 수 t입력
    cin >> t;

    //t개의 원의 반지름 r입력
    for (int idx = 1; idx <= t; idx++) {
        testcase(idx);
    }
    
    return 0;
}

문제5. 정주행

풀이

• 이 문제는 입력받은 n개의 정수를 정렬했을 때 arr[i+1] - arr[i] == 1가 된다면 연속된 수열로 표현할 수 있다고 판단한다.
• 간단히 data를 정렬해서 아래와 같은 코드로 판별해도 좋지만, 정렬된 결과를 출력하는 것이 아니므로 굳이 정렬을 할 필요가 없다.

//원소가 정렬되었을 때 연속된 수열로 표현되면 true 리턴
bool isConsecutive(int data[], int n) {
    
    for (int i = 0; i < n; i++) {
        for (int j = 1; j < n - i; j++) {
            if (data[j - 1] > data[j + 1]) {
                int temp = data[j];
                data[j] = data[j - 1];
                data[j - 1] = temp;
            }
        }
    }
    

    // 0 1 2 3 4 
    for (int i = 1; i < n; i++) {
        if (data[i] - data[i-1] > 1) {
            return false;
        }
    }
    return true;
}

• 이 방법보다는 현재 입력받을 원소의 개수는 n으로 정해져있고, 원소의 시작부터 끝까지 1씩만 증가되어야 한다.
• 따라서 원소의 시작(최소값)과 끝(최대값)을 구한 뒤, 끝-시작 == n-1이 되면 되는 것이다.
  ex) 1 2 5 3 4면 5-1==4 이므로 이를 만족하게 되는 것이다.
• 이렇게 정렬을 사용하지 않고 시간 복잡도를 크게 줄일 수 있다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

//N회의 에피소드를 순서없이 읽었다. 중복 에피소드를 보지는X
//읽은 에피소드 번호 차례로 주어지고, 
//이 번호 정렬시 연속된 수열로 표현되는지 판별

//원소가 정렬되었을 때 연속된 수열로 표현되면 true 리턴
bool isConsecutive(int data[], int n) {
    
    //정렬을 사용하지 않고, 
    //max - min = n(원소 개수)-1 이면 연속수열 가능!
    int max_data = data[0];
    int min_data = data[0];

    for (int i = 1; i < n; i++) {
        //최댓값 계산
        if (max_data < data[i]) {
            max_data = data[i];
        }
        //최소값 계산
        if (min_data > data[i]) {
            min_data = data[i];
        }
    }


    if (max_data - min_data == n - 1) {
        return true;//연속수열 가능
    }
    else {
        return false;//연속수열 불가능
    }
}


int main() {

    int n;
    int* data;

    //에피소드 수 n입력
    cin >> n;
    data = new int[n];

    //n개의 에피소드 번호 입력
    for (int i = 0; i < n; i++) {
        cin >> data[i];
    }
    
    bool result = isConsecutive(data, n);
    
    if (result) {
        printf("YES");
    }
    else {
        printf("NO");
    }

    delete[] data;
    return 0;
}