
최대공약수 알고리즘
최대공약수란?
두 수 A와 B의 공통된 약수 중에 가장 큰 정수
구하는 방법
초등학교에서 수학 배우던 시절로 돌아가 손으로 어떻게 계산했는지 떠올려보면 아래 이미지처럼 계산했더랬다.
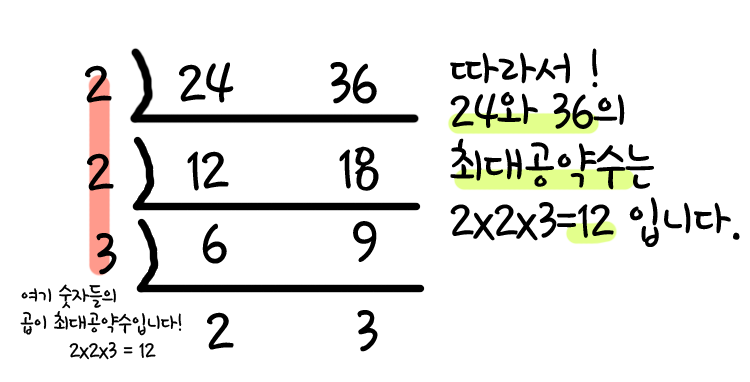
요컨대, 공통된 소수인 약수로 거듭해서 두 수를 나누었을 때 더이상 공통된 약수가 없는 시점에서 나누었던 약수들을 모두 곱하면 최대공약수가 된다는 것이다.
하지만 코드 창에서 저렇게 계산하고 있을 수는 없으니 다시 계산법을 생각해보자. 근본적인 계산법은 역시 2부터 두 수 중에 작은 값까지 모든 정수로 나눠보는 방법. 이걸로 의사 코드를 생각해보자.
Pseudo Code
function 최대공약수(a, b) {
최대공약수 변수 초기화;
for(2부터 a,b 중 작은 수까지 계속 ++) {
if(a도, b도 i로 나눠진다면) 최대공약수 변수 = i;
}
최대공약수 변수 반환
}실제 코드
이제 의사 코드를 가지고 실제 코드로 만들어보자.
// 근본적인 방법론
function getGCD(a, b) {
let gcd = 1;
for(let i = 2; i <= Math.min(a,b); i++) {
if(a % i === 0 && b % i === 0) gcd = i;
}
return gcd;
}
// 유클리드 호제법 + 재귀함수
let getGCD = (a, b) => (b > 0 ? getGCD(b, a % b) : a);
정석으로는 반복문을 사용해서 약수들을 구하는 방법도 있지만, 유클리드 호제법과 재귀함수를 사용해서 구하는 방법도 있다. 유클리드 호제법의 논리는 a와 b의 최대공약수가 b와 a를 b로 나눈 나머지의 최대공약수와 같다는 것이다.
최소공배수 알고리즘
최소공배수란?
두 수 A와 B의 공통된 배수 중에 가장 작은 정수
구하는 방법
최대공약수를 구했다면 가장 큰 산을 넘었다. 최소공배수는 최대공약수를 구한 다음 각 수를 나눠 나온 나머지를 최대공약수까지 포함해 곱하면 되기 때문이다.
Pseudo Code
function 최소공배수(a, b) {
최대공약수를 먼저 구한다.
// 최소공배수 = (a % 최대공약수) * (b % 최대공약수) * 최대공약수;
최소공배수 = a * b / 최대공약수
최소공배수 변수 반환
}실제 코드
function getLCM(a, b) {
let lcm = 1;
while(true) {
if(lcm % a === 0 && lcm % b === 0) break;
lcm++;
}
return lcm;
}
// 최대공약수 활용
let lcm = (a * b) / gcd;
유클리드 호제법으로 최대공약수를 구했다면 최소공배수를 구하는 건 알고리즘이랄 것까지도 없을 정도로 쉽다.
합성수 알고리즘
합성수 알고리즘은 문제로 생각해보게 되었는데 최대공약수와 중첩된 건가 싶은 느낌이었다.
합성수란?
약수의 갯수가 세 개 이상인 수
구하는 방법
먼저 합성수는 약수가 세 개 이상이라는 조건 때문에 4부터 시작한다. 4는 약수가 [1, 2, 4]로 가장 먼저 세 개 이상이라는 조건을 충족하는 정수다. 반복문을 4부터 시작해도 되겠지만, 어차피 1부터 시작하나 4부터 시작하나 성능 상 큰 차이가 있을 것 같지는 않았다. 그래서 배열 메서드를 활용해서 약수 갯수가 3개 미만인 것들을 걸러내는 방식으로 해보기로 했다.
의사 코드
function 합성수(n) {
배열 = 1~n까지 원소로 가지는 배열 생성;
배열.filter((v) => {
배열 원소를 반복문에서 i로 나눴을 때 나머지가 0이라면 카운트 변수++;
카운트가 3보다 큰 원소만 남김;
});
배열의 길이를 반환
}실제 코드
function solution(n) {
// Array.from()는 첫 인자로 배열을, 두번째 인자로 함수를 받아 map 함수의 역할을 해줄 수 있다.
let compositeArr = Array.from(Array(n), (v,i) => i+1).filter((i) => {
let cnt = 0;
for (let j = 1; j <= i; j++) {
if (i % j === 0) cnt++;
}
return cnt >= 3;
});
return compositeArr.length;
}